Discrete distributions are learnable from metastable samples

Markov chain samplers designed to sample from multi-variable distributions often undesirably get stuck in specific regions of their state space. This causes such samplers to approximately sample from a metastable distribution which is usually quite different from the desired, stationary distribution of the chain. We show that single-variable conditionals of metastable distributions of reversible Markov chain samplers that satisfy a strong metastability condition are on average very close to those of the true distribution. This holds even when the metastable distribution is far away from the true model in terms of global metrics like Kullback-Leibler divergence or total variation distance. This property allows us to learn the true model using a conditional likelihood based estimator, even when the samples come from a metastable distribution concentrated in a small region of the state space. Explicit examples of such metastable states can be constructed from regions that effectively bottleneck the probability flow and cause poor mixing of the Markov chain. For specific cases of binary pairwise undirected graphical models, we extend our results to further rigorously show that data coming from metastable states can be used to learn the parameters of the energy function and recover the structure of the model.

Optimization Proxies using Limited Labeled Data and Training Time -- A Semi-Supervised Bayesian Neural Network Approach

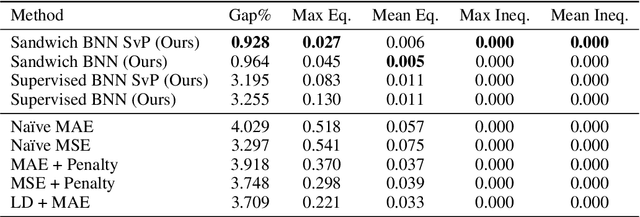
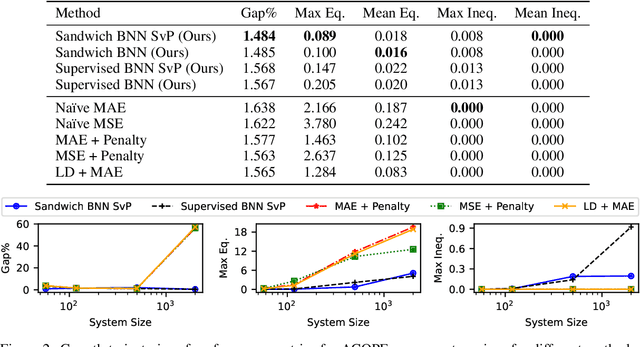
Constrained optimization problems arise in various engineering system operations such as inventory management and electric power grids. However, the requirement to repeatedly solve such optimization problems with uncertain parameters poses a significant computational challenge. This work introduces a learning scheme using Bayesian Neural Networks (BNNs) to solve constrained optimization problems under limited labeled data and restricted model training times. We propose a semi-supervised BNN for this practical but complex regime, wherein training commences in a sandwiched fashion, alternating between a supervised learning step (using labeled data) for minimizing cost, and an unsupervised learning step (using unlabeled data) for enforcing constraint feasibility. Both supervised and unsupervised steps use a Bayesian approach, where Stochastic Variational Inference is employed for approximate Bayesian inference. We show that the proposed semi-supervised learning method outperforms conventional BNN and deep neural network (DNN) architectures on important non-convex constrained optimization problems from energy network operations, achieving up to a tenfold reduction in expected maximum equality gap and halving the optimality and inequality (feasibility) gaps, without requiring any correction or projection step. By leveraging the BNN's ability to provide posterior samples at minimal computational cost, we demonstrate that a Selection via Posterior (SvP) scheme can further reduce equality gaps by more than 10%. We also provide tight and practically meaningful probabilistic confidence bounds that can be constructed using a low number of labeled testing data and readily adapted to other applications.

Data-Efficient Power Flow Learning for Network Contingencies

This work presents an efficient data-driven method to learn power flows in grids with network contingencies and to estimate corresponding probabilistic voltage envelopes (PVE). First, a network-aware Gaussian process (GP) termed Vertex-Degree Kernel (VDK-GP), developed in prior work, is used to estimate voltage-power functions for a few network configurations. The paper introduces a novel multi-task vertex degree kernel (MT-VDK) that amalgamates the learned VDK-GPs to determine power flows for unseen networks, with a significant reduction in the computational complexity and hyperparameter requirements compared to alternate approaches. Simulations on the IEEE 30-Bus network demonstrate the retention and transfer of power flow knowledge in both N-1 and N-2 contingency scenarios. The MT-VDK-GP approach achieves over 50% reduction in mean prediction error for novel N-1 contingency network configurations in low training data regimes (50-250 samples) over VDK-GP. Additionally, MT-VDK-GP outperforms a hyper-parameter based transfer learning approach in over 75% of N-2 contingency network structures, even without historical N-2 outage data. The proposed method demonstrates the ability to achieve PVEs using sixteen times fewer power flow solutions compared to Monte-Carlo sampling-based methods.

Graph-Structured Kernel Design for Power Flow Learning using Gaussian Processes

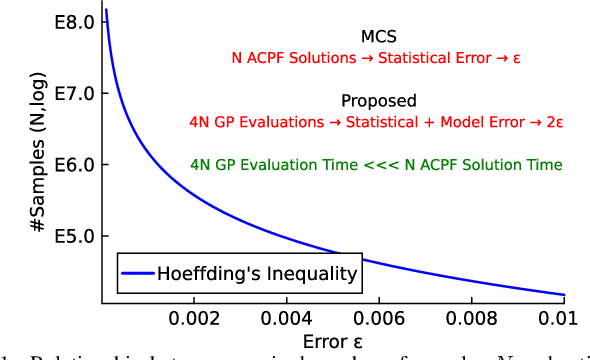
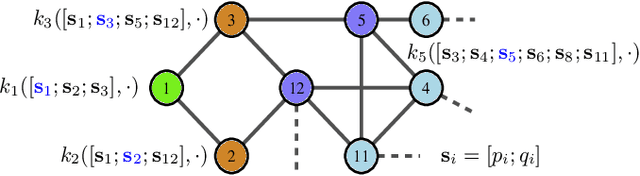
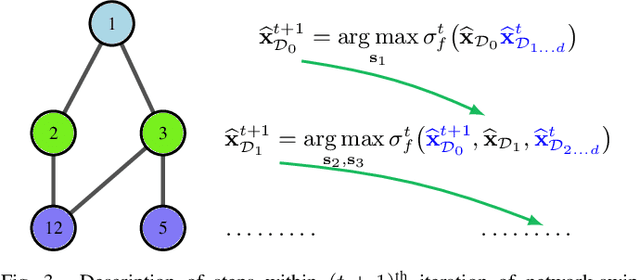
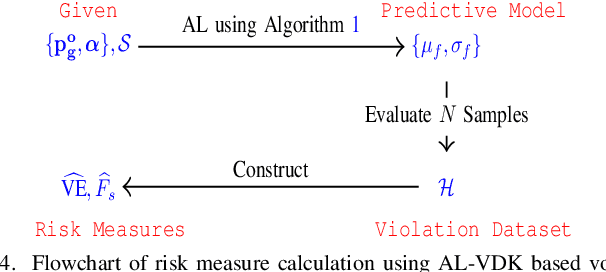
This paper presents a physics-inspired graph-structured kernel designed for power flow learning using Gaussian Process (GP). The kernel, named the vertex-degree kernel (VDK), relies on latent decomposition of voltage-injection relationship based on the network graph or topology. Notably, VDK design avoids the need to solve optimization problems for kernel search. To enhance efficiency, we also explore a graph-reduction approach to obtain a VDK representation with lesser terms. Additionally, we propose a novel network-swipe active learning scheme, which intelligently selects sequential training inputs to accelerate the learning of VDK. Leveraging the additive structure of VDK, the active learning algorithm performs a block-descent type procedure on GP's predictive variance, serving as a proxy for information gain. Simulations demonstrate that the proposed VDK-GP achieves more than two fold sample complexity reduction, compared to full GP on medium scale 500-Bus and large scale 1354-Bus power systems. The network-swipe algorithm outperforms mean performance of 500 random trials on test predictions by two fold for medium-sized 500-Bus systems and best performance of 25 random trials for large-scale 1354-Bus systems by 10%. Moreover, we demonstrate that the proposed method's performance for uncertainty quantification applications with distributionally shifted testing data sets.

DNN-based Policies for Stochastic AC OPF

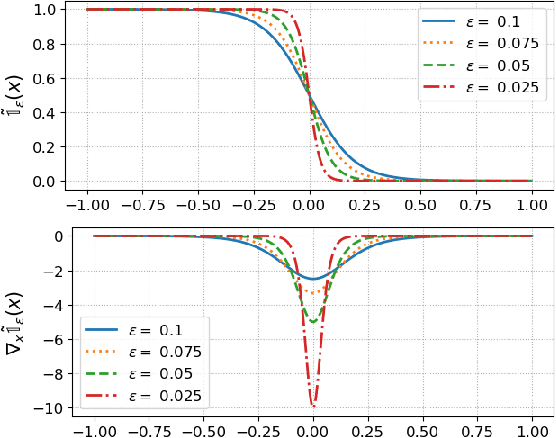
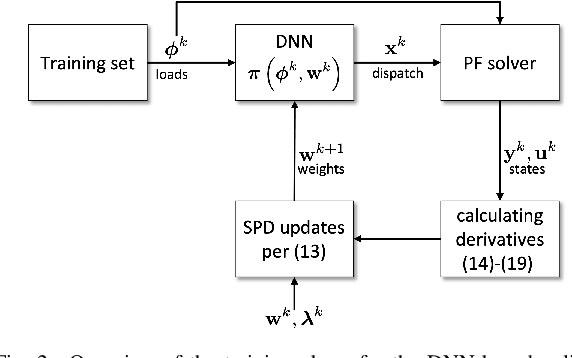
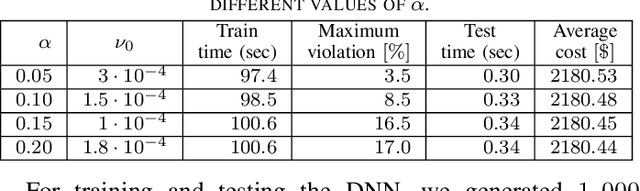
A prominent challenge to the safe and optimal operation of the modern power grid arises due to growing uncertainties in loads and renewables. Stochastic optimal power flow (SOPF) formulations provide a mechanism to handle these uncertainties by computing dispatch decisions and control policies that maintain feasibility under uncertainty. Most SOPF formulations consider simple control policies such as affine policies that are mathematically simple and resemble many policies used in current practice. Motivated by the efficacy of machine learning (ML) algorithms and the potential benefits of general control policies for cost and constraint enforcement, we put forth a deep neural network (DNN)-based policy that predicts the generator dispatch decisions in real time in response to uncertainty. The weights of the DNN are learnt using stochastic primal-dual updates that solve the SOPF without the need for prior generation of training labels and can explicitly account for the feasibility constraints in the SOPF. The advantages of the DNN policy over simpler policies and their efficacy in enforcing safety limits and producing near optimal solutions are demonstrated in the context of a chance constrained formulation on a number of test cases.

Exponential Reduction in Sample Complexity with Learning of Ising Model Dynamics

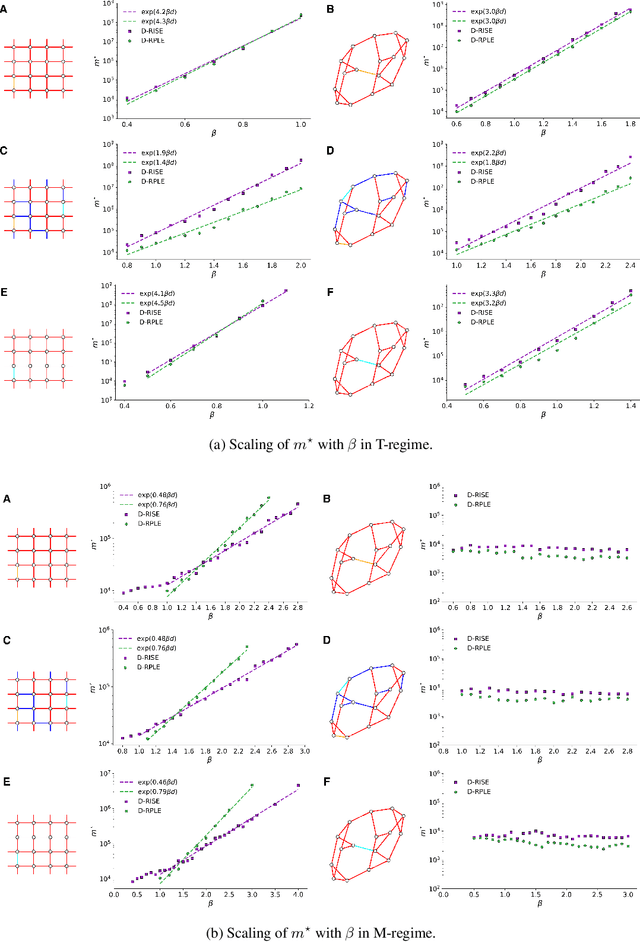
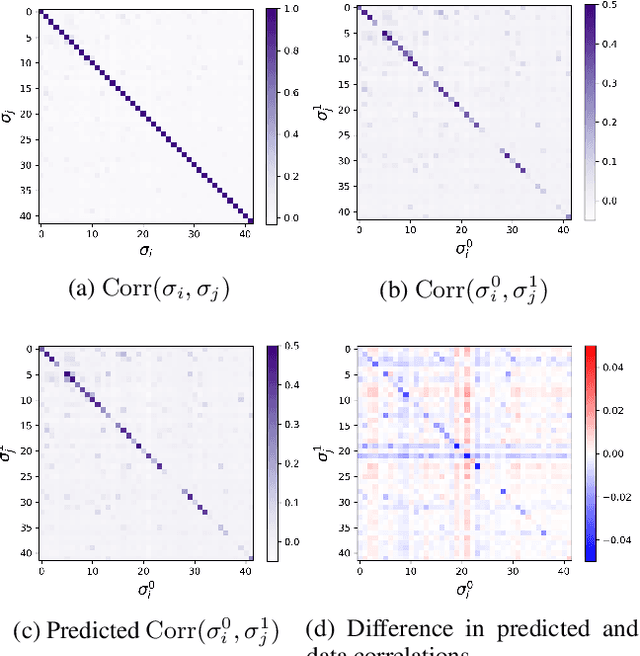
The usual setting for learning the structure and parameters of a graphical model assumes the availability of independent samples produced from the corresponding multivariate probability distribution. However, for many models the mixing time of the respective Markov chain can be very large and i.i.d. samples may not be obtained. We study the problem of reconstructing binary graphical models from correlated samples produced by a dynamical process, which is natural in many applications. We analyze the sample complexity of two estimators that are based on the interaction screening objective and the conditional likelihood loss. We observe that for samples coming from a dynamical process far from equilibrium, the sample complexity reduces exponentially compared to a dynamical process that mixes quickly.

Learning Continuous Exponential Families Beyond Gaussian

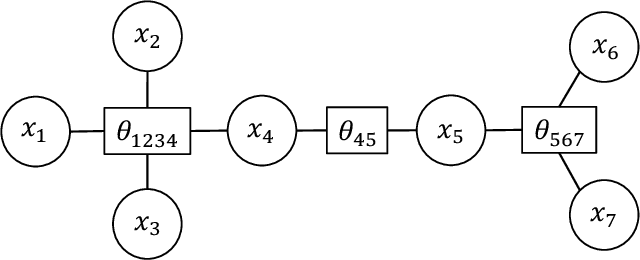
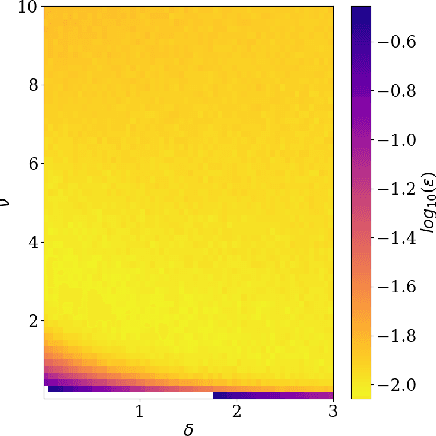
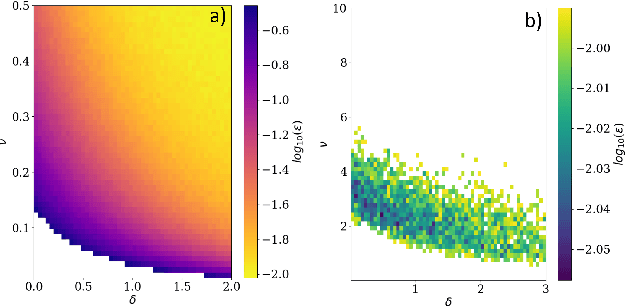
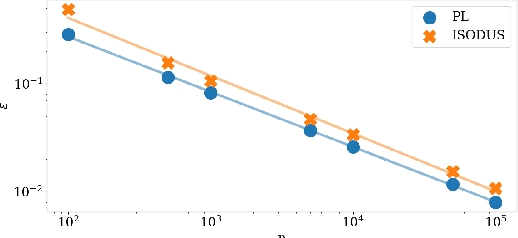
We address the problem of learning of continuous exponential family distributions with unbounded support. While a lot of progress has been made on learning of Gaussian graphical models, we are still lacking scalable algorithms for reconstructing general continuous exponential families modeling higher-order moments of the data beyond the mean and the covariance. Here, we introduce a computationally efficient method for learning continuous graphical models based on the Interaction Screening approach. Through a series of numerical experiments, we show that our estimator maintains similar requirements in terms of accuracy and sample complexity compared to alternative approaches such as maximization of conditional likelihood, while considerably improving upon the algorithm's run-time.

Learning of Discrete Graphical Models with Neural Networks

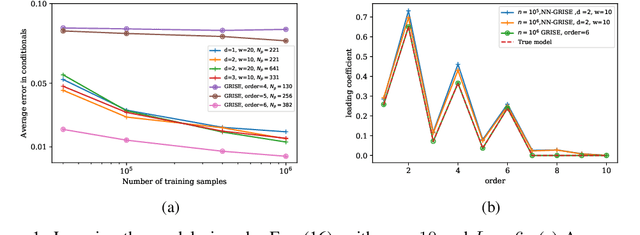
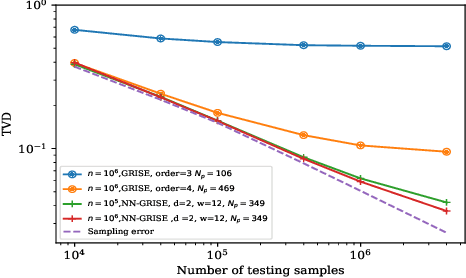
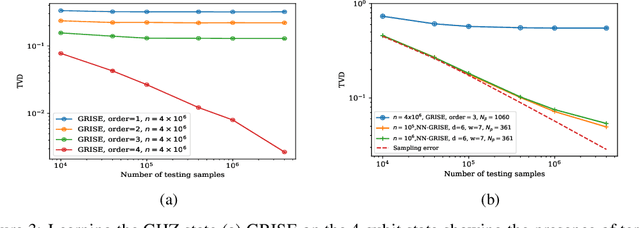
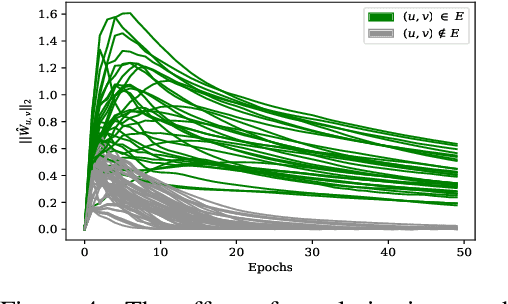
Graphical models are widely used in science to represent joint probability distributions with an underlying conditional dependence structure. The inverse problem of learning a discrete graphical model given i.i.d samples from its joint distribution can be solved with near-optimal sample complexity using a convex optimization method known as Generalized Regularized Interaction Screening Estimator (GRISE). But the computational cost of GRISE becomes prohibitive when the energy function of the true graphical model has higher order terms. We introduce NN-GRISE, a neural net based algorithm for graphical model learning, to tackle this limitation of GRISE. We use neural nets as function approximators in an interaction screening objective function. The optimization of this objective then produces a neural-net representation for the conditionals of the graphical model. NN-GRISE algorithm is seen to be a better alternative to GRISE when the energy function of the true model has a high order with a high degree of symmetry. In these cases, NN-GRISE is able to find the correct parsimonious representation for the conditionals without being fed any prior information about the true model. NN-GRISE can also be used to learn the underlying structure of the true model with some simple modifications to its training procedure. In addition, we also show a variant of NN-GRISE that can be used to learn a neural net representation for the full energy function of the true model.

Tractable learning in under-excited power grids

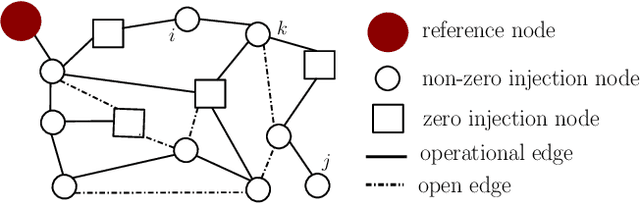
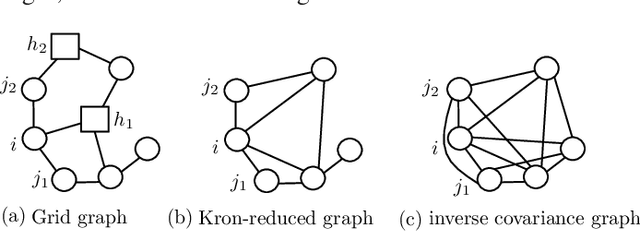
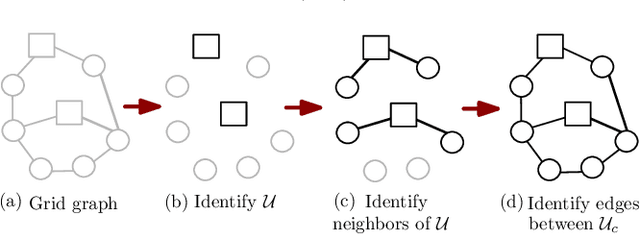
Estimating the structure of physical flow networks such as power grids is critical to secure delivery of energy. This paper discusses statistical structure estimation in power grids in the "under-excited" regime, where a subset of internal nodes do not have external injection. Prior estimation algorithms based on nodal potentials or voltages fail in the under-excited regime. We propose a novel topology learning algorithm for learning underexcited general (non-radial) networks based on physics-informed conservation laws. We prove the asymptotic correctness of our algorithm for grids with non-adjacent under-excited internal nodes. More importantly, we theoretically analyze our algorithm's efficacy under noisy measurements, and determine bounds on maximum noise under which asymptotically correct recovery is guaranteed. Our approach is validated through simulations with non-linear voltage samples generated on test grids with real injection data

Efficient Learning of Discrete Graphical Models

Graphical models are useful tools for describing structured high-dimensional probability distributions. Development of efficient algorithms for learning graphical models with least amount of data remains an active research topic. Reconstruction of graphical models that describe the statistics of discrete variables is a particularly challenging problem, for which the maximum likelihood approach is intractable. In this work, we provide the first sample-efficient method based on the Interaction Screening framework that allows one to provably learn fully general discrete factor models with node-specific discrete alphabets and multi-body interactions, specified in an arbitrary basis. We identify a single condition related to model parametrization that leads to rigorous guarantees on the recovery of model structure and parameters in any error norm, and is readily verifiable for a large class of models. Importantly, our bounds make explicit distinction between parameters that are proper to the model and priors used as an input to the algorithm. Finally, we show that the Interaction Screening framework includes all models previously considered in the literature as special cases, and for which our analysis shows a systematic improvement in sample complexity.