Sample Complexity Bounds for Robustly Learning Decision Lists against Evasion Attacks

A fundamental problem in adversarial machine learning is to quantify how much training data is needed in the presence of evasion attacks. In this paper we address this issue within the framework of PAC learning, focusing on the class of decision lists. Given that distributional assumptions are essential in the adversarial setting, we work with probability distributions on the input data that satisfy a Lipschitz condition: nearby points have similar probability. Our key results illustrate that the adversary's budget (that is, the number of bits it can perturb on each input) is a fundamental quantity in determining the sample complexity of robust learning. Our first main result is a sample-complexity lower bound: the class of monotone conjunctions (essentially the simplest non-trivial hypothesis class on the Boolean hypercube) and any superclass has sample complexity at least exponential in the adversary's budget. Our second main result is a corresponding upper bound: for every fixed $k$ the class of $k$-decision lists has polynomial sample complexity against a $\log(n)$-bounded adversary. This sheds further light on the question of whether an efficient PAC learning algorithm can always be used as an efficient $\log(n)$-robust learning algorithm under the uniform distribution.

Exponential Tail Local Rademacher Complexity Risk Bounds Without the Bernstein Condition

The local Rademacher complexity framework is one of the most successful general-purpose toolboxes for establishing sharp excess risk bounds for statistical estimators based on the framework of empirical risk minimization. Applying this toolbox typically requires using the Bernstein condition, which often restricts applicability to convex and proper settings. Recent years have witnessed several examples of problems where optimal statistical performance is only achievable via non-convex and improper estimators originating from aggregation theory, including the fundamental problem of model selection. These examples are currently outside of the reach of the classical localization theory. In this work, we build upon the recent approach to localization via offset Rademacher complexities, for which a general high-probability theory has yet to be established. Our main result is an exponential-tail excess risk bound expressed in terms of the offset Rademacher complexity that yields results at least as sharp as those obtainable via the classical theory. However, our bound applies under an estimator-dependent geometric condition (the "offset condition") instead of the estimator-independent (but, in general, distribution-dependent) Bernstein condition on which the classical theory relies. Our results apply to improper prediction regimes not directly covered by the classical theory.

Towards optimally abstaining from prediction

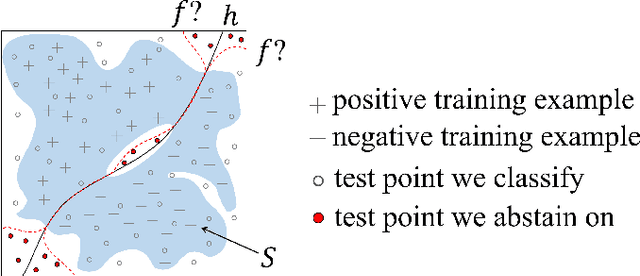
A common challenge across all areas of machine learning is that training data is not distributed like test data, due to natural shifts, "blind spots," or adversarial examples. We consider a model where one may abstain from predicting, at a fixed cost. In particular, our transductive abstention algorithm takes labeled training examples and unlabeled test examples as input, and provides predictions with optimal prediction loss guarantees. The loss bounds match standard generalization bounds when test examples are i.i.d. from the training distribution, but add an additional term that is the cost of abstaining times the statistical distance between the train and test distribution (or the fraction of adversarial examples). For linear regression, we give a polynomial-time algorithm based on Celis-Dennis-Tapia optimization algorithms. For binary classification, we show how to efficiently implement it using a proper agnostic learner (i.e., an Empirical Risk Minimizer) for the class of interest. Our work builds on a recent abstention algorithm of Goldwasser, Kalais, and Montasser (2020) for transductive binary classification.

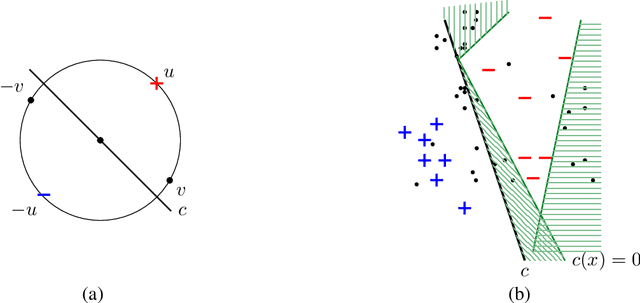
Efficient Learning with Arbitrary Covariate Shift

We give an efficient algorithm for learning a binary function in a given class C of bounded VC dimension, with training data distributed according to P and test data according to Q, where P and Q may be arbitrary distributions over X. This is the generic form of what is called covariate shift, which is impossible in general as arbitrary P and Q may not even overlap. However, recently guarantees were given in a model called PQ-learning (Goldwasser et al., 2020) where the learner has: (a) access to unlabeled test examples from Q (in addition to labeled samples from P, i.e., semi-supervised learning); and (b) the option to reject any example and abstain from classifying it (i.e., selective classification). The algorithm of Goldwasser et al. (2020) requires an (agnostic) noise tolerant learner for C. The present work gives a polynomial-time PQ-learning algorithm that uses an oracle to a "reliable" learner for C, where reliable learning (Kalai et al., 2012) is a model of learning with one-sided noise. Furthermore, our reduction is optimal in the sense that we show the equivalence of reliable and PQ learning.

Lottery Tickets in Linear Models: An Analysis of Iterative Magnitude Pruning

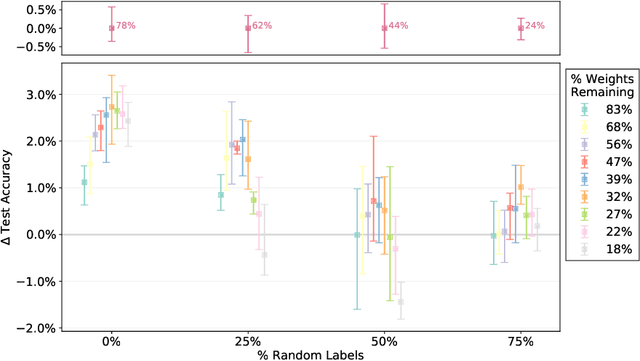
We analyse the pruning procedure behind the lottery ticket hypothesis arXiv:1803.03635v5, iterative magnitude pruning (IMP), when applied to linear models trained by gradient flow. We begin by presenting sufficient conditions on the statistical structure of the features, under which IMP prunes those features that have smallest projection onto the data. Following this, we explore IMP as a method for sparse estimation and sparse prediction in noisy settings, with minimal assumptions on the design matrix. The same techniques are then applied to derive corresponding results for threshold pruning. Finally, we present experimental evidence of the regularising effect of IMP. We hope that our work will contribute to a theoretically grounded understanding of lottery tickets and how they emerge from IMP.

How benign is benign overfitting?

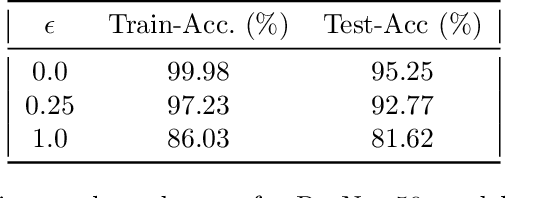
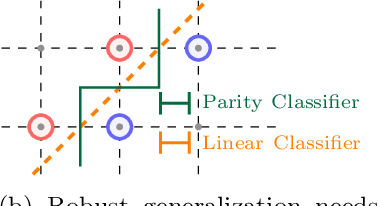
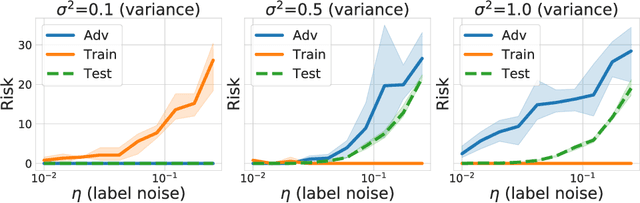
We investigate two causes for adversarial vulnerability in deep neural networks: bad data and (poorly) trained models. When trained with SGD, deep neural networks essentially achieve zero training error, even in the presence of label noise, while also exhibiting good generalization on natural test data, something referred to as benign overfitting [2, 10]. However, these models are vulnerable to adversarial attacks. We identify label noise as one of the causes for adversarial vulnerability, and provide theoretical and empirical evidence in support of this. Surprisingly, we find several instances of label noise in datasets such as MNIST and CIFAR, and that robustly trained models incur training error on some of these, i.e. they don't fit the noise. However, removing noisy labels alone does not suffice to achieve adversarial robustness. Standard training procedures bias neural networks towards learning "simple" classification boundaries, which may be less robust than more complex ones. We observe that adversarial training does produce more complex decision boundaries. We conjecture that in part the need for complex decision boundaries arises from sub-optimal representation learning. By means of simple toy examples, we show theoretically how the choice of representation can drastically affect adversarial robustness.

Differentiable Causal Backdoor Discovery

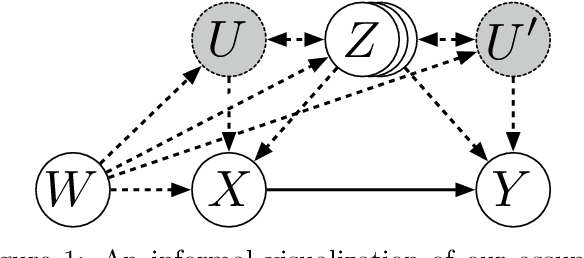
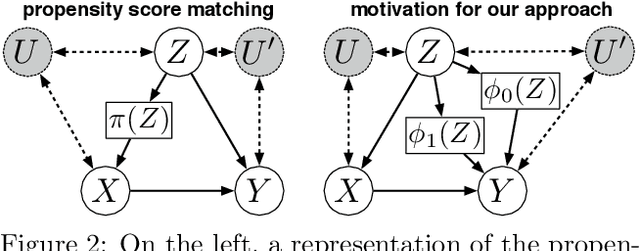
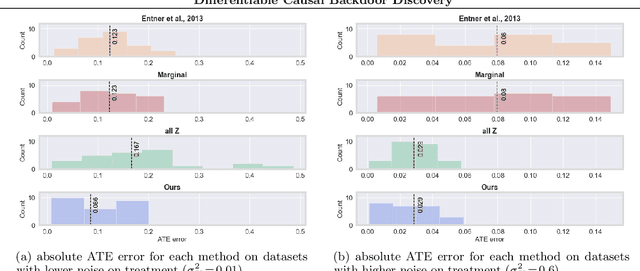
Discovering the causal effect of a decision is critical to nearly all forms of decision-making. In particular, it is a key quantity in drug development, in crafting government policy, and when implementing a real-world machine learning system. Given only observational data, confounders often obscure the true causal effect. Luckily, in some cases, it is possible to recover the causal effect by using certain observed variables to adjust for the effects of confounders. However, without access to the true causal model, finding this adjustment requires brute-force search. In this work, we present an algorithm that exploits auxiliary variables, similar to instruments, in order to find an appropriate adjustment by a gradient-based optimization method. We demonstrate that it outperforms practical alternatives in estimating the true causal effect, without knowledge of the full causal graph.

The Statistical Complexity of Early Stopped Mirror Descent

Recently there has been a surge of interest in understanding implicit regularization properties of iterative gradient-based optimization algorithms. In this paper, we study the statistical guarantees on the excess risk achieved by early stopped unconstrained mirror descent algorithms applied to the unregularized empirical risk with squared loss for linear models and kernel methods. We identify a link between offset Rademacher complexities and potential-based analysis of mirror descent that allows disentangling statistics from optimization in the analysis of such algorithms. Our main result characterizes the statistical performance of the path traced by the iterates of mirror descent in terms of offset complexities of certain function classes depending only on the choice of the mirror map, initialization point, step-size, and number of iterations. We apply our theory to recover, in a rather clean and elegant manner, some of the recent results in the implicit regularization literature, while also showing how to improve upon them in some settings.

Online k-means Clustering

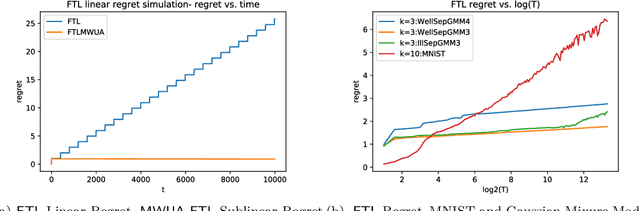
We study the problem of online clustering where a clustering algorithm has to assign a new point that arrives to one of $k$ clusters. The specific formulation we use is the $k$-means objective: At each time step the algorithm has to maintain a set of k candidate centers and the loss incurred is the squared distance between the new point and the closest center. The goal is to minimize regret with respect to the best solution to the $k$-means objective ($\mathcal{C}$) in hindsight. We show that provided the data lies in a bounded region, an implementation of the Multiplicative Weights Update Algorithm (MWUA) using a discretized grid achieves a regret bound of $\tilde{O}(\sqrt{T})$ in expectation. We also present an online-to-offline reduction that shows that an efficient no-regret online algorithm (despite being allowed to choose a different set of candidate centres at each round) implies an offline efficient algorithm for the $k$-means problem. In light of this hardness, we consider the slightly weaker requirement of comparing regret with respect to $(1 + \epsilon) \mathcal{C}$ and present a no-regret algorithm with runtime $O\left(T(\mathrm{poly}(log(T),k,d,1/\epsilon)^{k(d+O(1))}\right)$. Our algorithm is based on maintaining an incremental coreset and an adaptive variant of the MWUA. We show that na\"{i}ve online algorithms, such as \emph{Follow The Leader}, fail to produce sublinear regret in the worst case. We also report preliminary experiments with synthetic and real-world data.

On the Hardness of Robust Classification

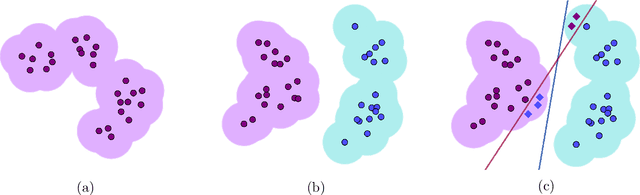
It is becoming increasingly important to understand the vulnerability of machine learning models to adversarial attacks. In this paper we study the feasibility of robust learning from the perspective of computational learning theory, considering both sample and computational complexity. In particular, our definition of robust learnability requires polynomial sample complexity. We start with two negative results. We show that no non-trivial concept class can be robustly learned in the distribution-free setting against an adversary who can perturb just a single input bit. We show moreover that the class of monotone conjunctions cannot be robustly learned under the uniform distribution against an adversary who can perturb $\omega(\log n)$ input bits. However if the adversary is restricted to perturbing $O(\log n)$ bits, then the class of monotone conjunctions can be robustly learned with respect to a general class of distributions (that includes the uniform distribution). Finally, we provide a simple proof of the computational hardness of robust learning on the boolean hypercube. Unlike previous results of this nature, our result does not rely on another computational model (e.g. the statistical query model) nor on any hardness assumption other than the existence of a hard learning problem in the PAC framework.