U-Clip: On-Average Unbiased Stochastic Gradient Clipping

U-Clip is a simple amendment to gradient clipping that can be applied to any iterative gradient optimization algorithm. Like regular clipping, U-Clip involves using gradients that are clipped to a prescribed size (e.g. with component wise or norm based clipping) but instead of discarding the clipped portion of the gradient, U-Clip maintains a buffer of these values that is added to the gradients on the next iteration (before clipping). We show that the cumulative bias of the U-Clip updates is bounded by a constant. This implies that the clipped updates are unbiased on average. Convergence follows via a lemma that guarantees convergence with updates $u_i$ as long as $\sum_{i=1}^t (u_i - g_i) = o(t)$ where $g_i$ are the gradients. Extensive experimental exploration is performed on CIFAR10 with further validation given on ImageNet.

Provably Strict Generalisation Benefit for Invariance in Kernel Methods

It is a commonly held belief that enforcing invariance improves generalisation. Although this approach enjoys widespread popularity, it is only very recently that a rigorous theoretical demonstration of this benefit has been established. In this work we build on the function space perspective of Elesedy and Zaidi arXiv:2102.10333 to derive a strictly non-zero generalisation benefit of incorporating invariance in kernel ridge regression when the target is invariant to the action of a compact group. We study invariance enforced by feature averaging and find that generalisation is governed by a notion of effective dimension that arises from the interplay between the kernel and the group. In building towards this result, we find that the action of the group induces an orthogonal decomposition of both the reproducing kernel Hilbert space and its kernel, which may be of interest in its own right.

Provably Strict Generalisation Benefit for Equivariant Models

It is widely believed that engineering a model to be invariant/equivariant improves generalisation. Despite the growing popularity of this approach, a precise characterisation of the generalisation benefit is lacking. By considering the simplest case of linear models, this paper provides the first provably non-zero improvement in generalisation for invariant/equivariant models when the target distribution is invariant/equivariant with respect to a compact group. Moreover, our work reveals an interesting relationship between generalisation, the number of training examples and properties of the group action. Our results rest on an observation of the structure of function spaces under averaging operators which, along with its consequences for feature averaging, may be of independent interest.

Lottery Tickets in Linear Models: An Analysis of Iterative Magnitude Pruning

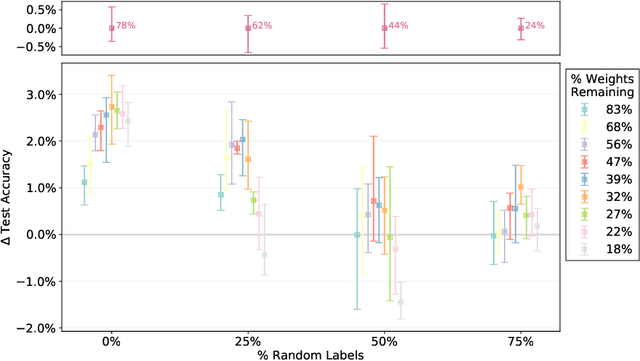
We analyse the pruning procedure behind the lottery ticket hypothesis arXiv:1803.03635v5, iterative magnitude pruning (IMP), when applied to linear models trained by gradient flow. We begin by presenting sufficient conditions on the statistical structure of the features, under which IMP prunes those features that have smallest projection onto the data. Following this, we explore IMP as a method for sparse estimation and sparse prediction in noisy settings, with minimal assumptions on the design matrix. The same techniques are then applied to derive corresponding results for threshold pruning. Finally, we present experimental evidence of the regularising effect of IMP. We hope that our work will contribute to a theoretically grounded understanding of lottery tickets and how they emerge from IMP.