Torsten A. Enßlin
Max-Planck Institut für Astrophysik, Ludwig-Maximilians-Universität München
Re-Envisioning Numerical Information Field Theory (NIFTy.re): A Library for Gaussian Processes and Variational Inference
Feb 26, 2024Abstract:Imaging is the process of transforming noisy, incomplete data into a space that humans can interpret. NIFTy is a Bayesian framework for imaging and has already successfully been applied to many fields in astrophysics. Previous design decisions held the performance and the development of methods in NIFTy back. We present a rewrite of NIFTy, coined NIFTy.re, which reworks the modeling principle, extends the inference strategies, and outsources much of the heavy lifting to JAX. The rewrite dramatically accelerates models written in NIFTy, lays the foundation for new types of inference machineries, improves maintainability, and enables interoperability between NIFTy and the JAX machine learning ecosystem.
Sparse Kernel Gaussian Processes through Iterative Charted Refinement (ICR)
Jun 21, 2022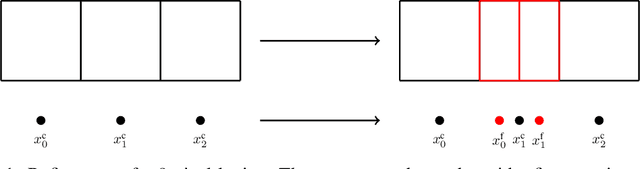
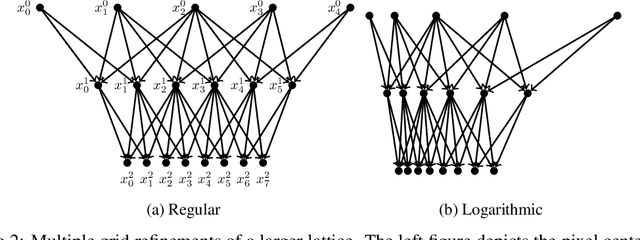
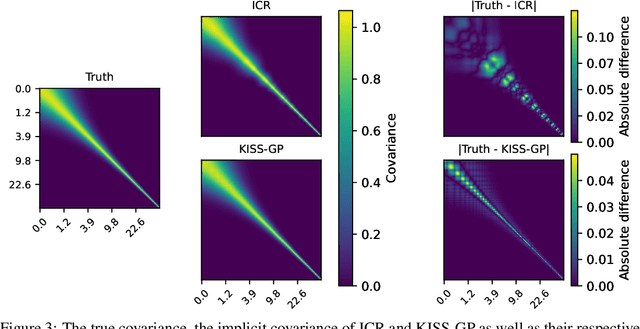
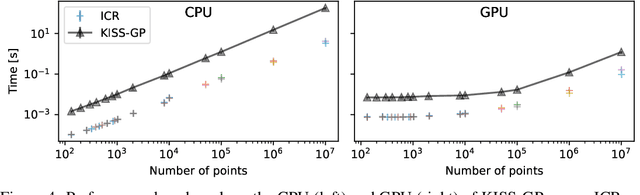
Abstract:Gaussian Processes (GPs) are highly expressive, probabilistic models. A major limitation is their computational complexity. Naively, exact GP inference requires $\mathcal{O}(N^3)$ computations with $N$ denoting the number of modeled points. Current approaches to overcome this limitation either rely on sparse, structured or stochastic representations of data or kernel respectively and usually involve nested optimizations to evaluate a GP. We present a new, generative method named Iterative Charted Refinement (ICR) to model GPs on nearly arbitrarily spaced points in $\mathcal{O}(N)$ time for decaying kernels without nested optimizations. ICR represents long- as well as short-range correlations by combining views of the modeled locations at varying resolutions with a user-provided coordinate chart. In our experiment with points whose spacings vary over two orders of magnitude, ICR's accuracy is comparable to state-of-the-art GP methods. ICR outperforms existing methods in terms of computational speed by one order of magnitude on the CPU and GPU and has already been successfully applied to model a GP with $122$ billion parameters.
Probabilistic Autoencoder using Fisher Information
Oct 28, 2021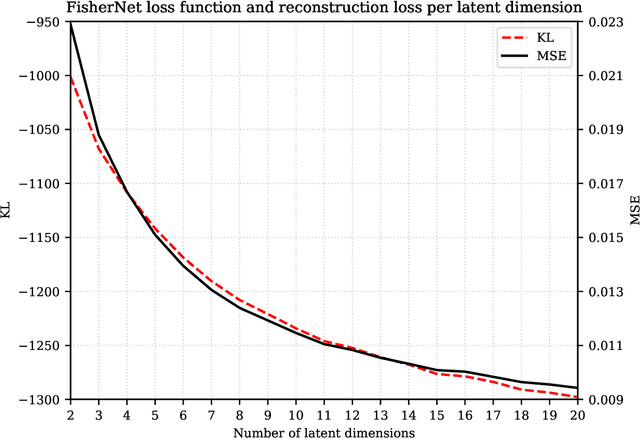
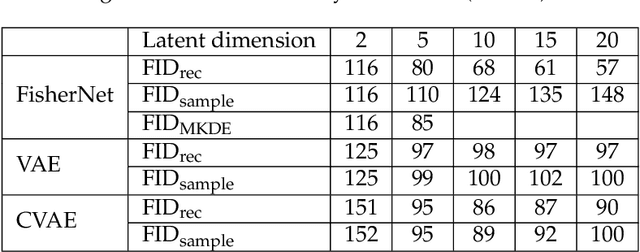
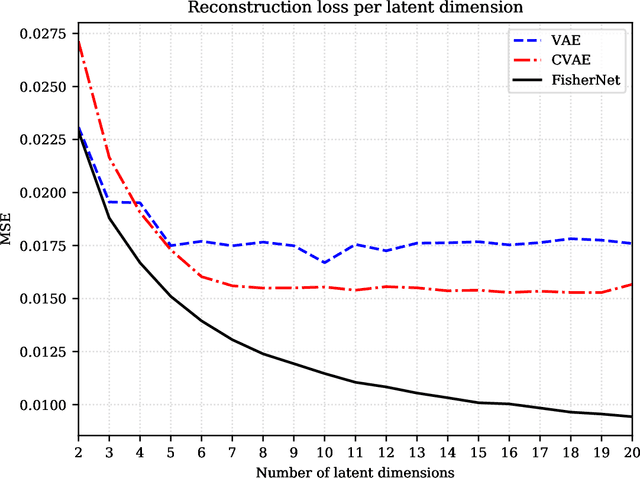

Abstract:Neural Networks play a growing role in many science disciplines, including physics. Variational Autoencoders (VAEs) are neural networks that are able to represent the essential information of a high dimensional data set in a low dimensional latent space, which have a probabilistic interpretation. In particular the so-called encoder network, the first part of the VAE, which maps its input onto a position in latent space, additionally provides uncertainty information in terms of a variance around this position. In this work, an extension to the Autoencoder architecture is introduced, the FisherNet. In this architecture, the latent space uncertainty is not generated using an additional information channel in the encoder, but derived from the decoder, by means of the Fisher information metric. This architecture has advantages from a theoretical point of view as it provides a direct uncertainty quantification derived from the model, and also accounts for uncertainty cross-correlations. We can show experimentally that the FisherNet produces more accurate data reconstructions than a comparable VAE and its learning performance also apparently scales better with the number of latent space dimensions.
Geometric variational inference
May 21, 2021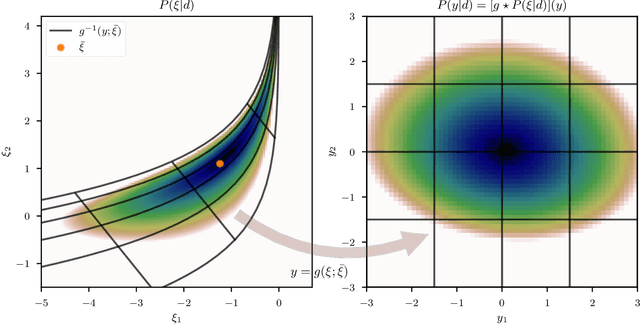
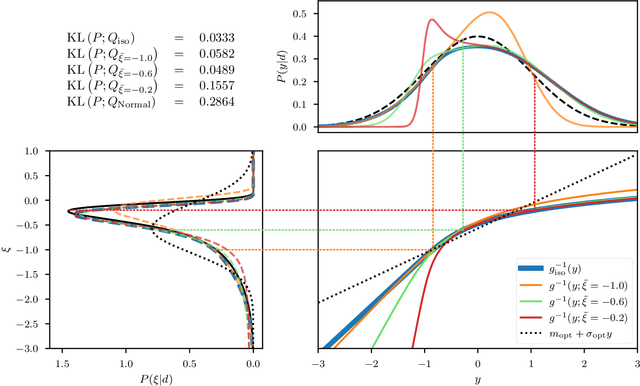
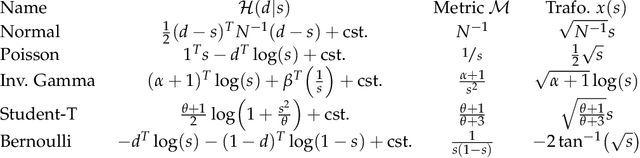
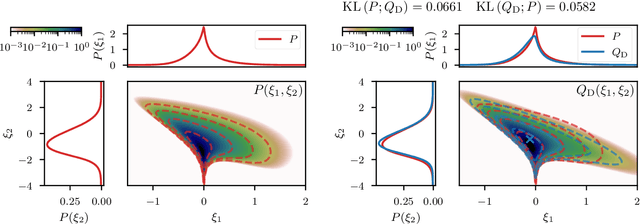
Abstract:Efficiently accessing the information contained in non-linear and high dimensional probability distributions remains a core challenge in modern statistics. Traditionally, estimators that go beyond point estimates are either categorized as Variational Inference (VI) or Markov-Chain Monte-Carlo (MCMC) techniques. While MCMC methods that utilize the geometric properties of continuous probability distributions to increase their efficiency have been proposed, VI methods rarely use the geometry. This work aims to fill this gap and proposes geometric Variational Inference (geoVI), a method based on Riemannian geometry and the Fisher information metric. It is used to construct a coordinate transformation that relates the Riemannian manifold associated with the metric to Euclidean space. The distribution, expressed in the coordinate system induced by the transformation, takes a particularly simple form that allows for an accurate variational approximation by a normal distribution. Furthermore, the algorithmic structure allows for an efficient implementation of geoVI which is demonstrated on multiple examples, ranging from low-dimensional illustrative ones to non-linear, hierarchical Bayesian inverse problems in thousands of dimensions.
Metric Gaussian Variational Inference
Jan 30, 2019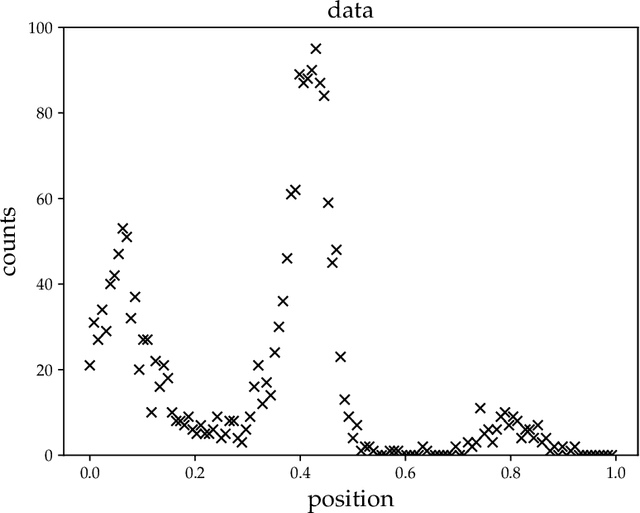

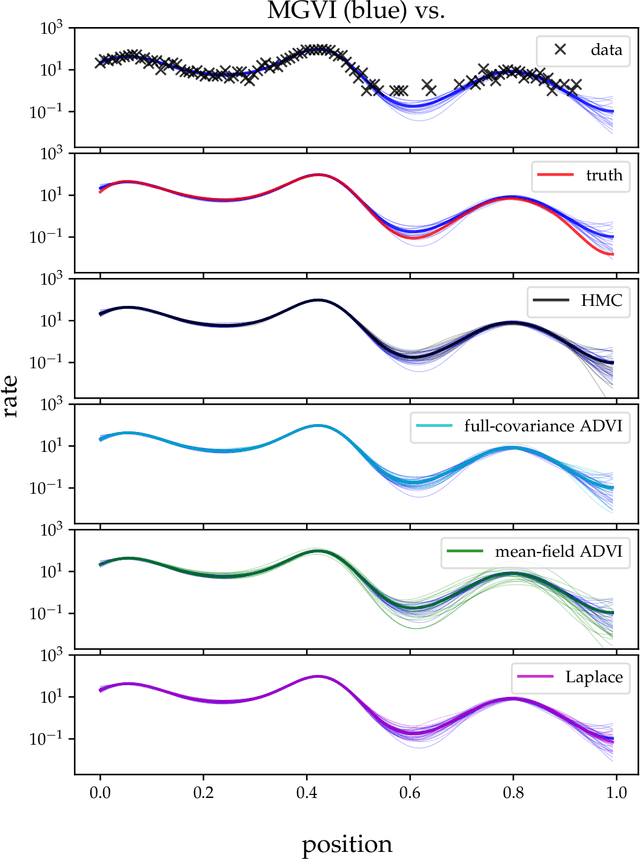
Abstract:A variational Gaussian approximation of the posterior distribution can be an excellent way to infer posterior quantities. However, to capture all posterior correlations the parametrization of the full covariance is required, which scales quadratic with the problem size. This scaling prohibits full-covariance approximations for large-scale problems. As a solution to this limitation we propose Metric Gaussian Variational Inference (MGVI). This procedure approximates the variational covariance such that it requires no parameters on its own and still provides reliable posterior correlations and uncertainties for all model parameters. We approximate the variational covariance with the inverse Fisher metric, a local estimate of the true posterior uncertainty. This covariance is only stored implicitly and all necessary quantities can be extracted from it by independent samples drawn from the approximating Gaussian. MGVI requires the minimization of a stochastic estimate of the Kullback-Leibler divergence only with respect to the mean of the variational Gaussian, a quantity that only scales linearly with the problem size. We motivate the choice of this covariance from an information geometric perspective. The method is validated against established approaches in a small example and the scaling is demonstrated in a problem with over a million parameters.
Bayesian Causal Inference
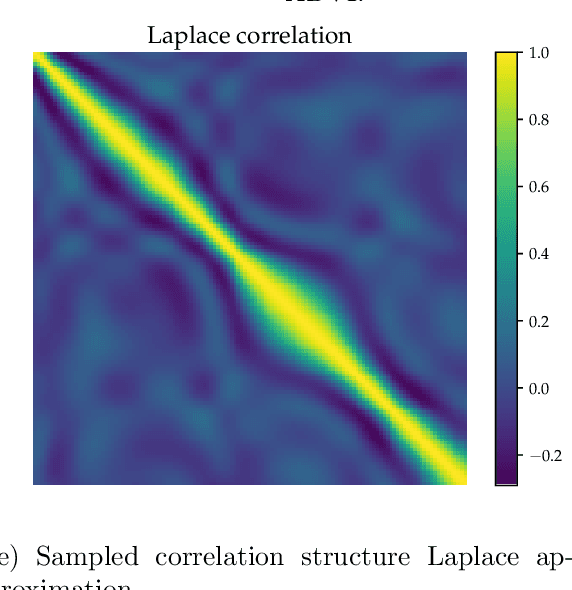
Dec 24, 2018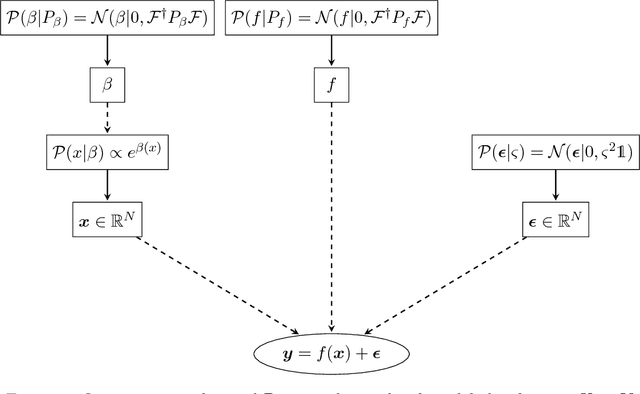
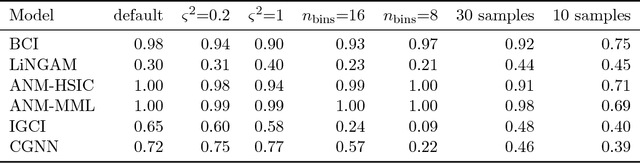
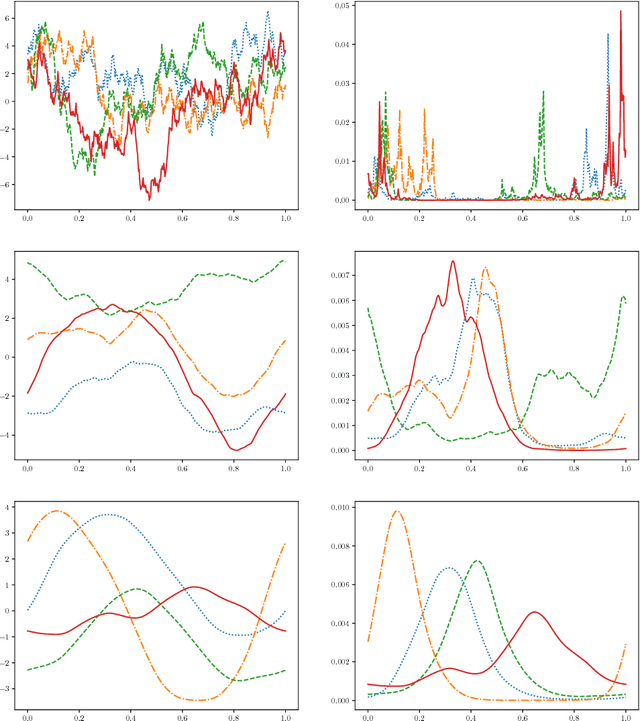
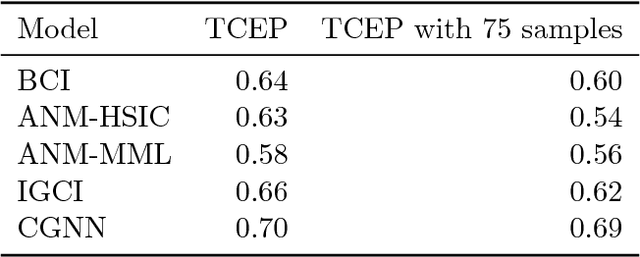
Abstract:We address the problem of two-variable causal inference. This task is to infer an existing causal relation between two random variables, i.e. $X \rightarrow Y$ or $Y \rightarrow X$, from purely observational data. We briefly review a number of state-of-the-art methods for this, including very recent ones. A novel inference method is introduced, Bayesian Causal Inference (BCI), which assumes a generative Bayesian hierarchical model to pursue the strategy of Bayesian model selection. In the model the distribution of the cause variable is given by a Poisson lognormal distribution, which allows to explicitly regard discretization effects. We assume Fourier diagonal Field covariance operators. The generative model assumed provides synthetic causal data for benchmarking our model in comparison to existing State-of-the-art models, namely LiNGAM, ANM-HSIC, ANM-MML, IGCI and CGNN. We explore how well the above methods perform in case of high noise settings, strongly discretized data and very sparse data. BCI performs generally reliable with synthetic data as well as with the real world TCEP benchmark set, with an accuracy comparable to state-of-the-art algorithms.
Encoding prior knowledge in the structure of the likelihood
Dec 11, 2018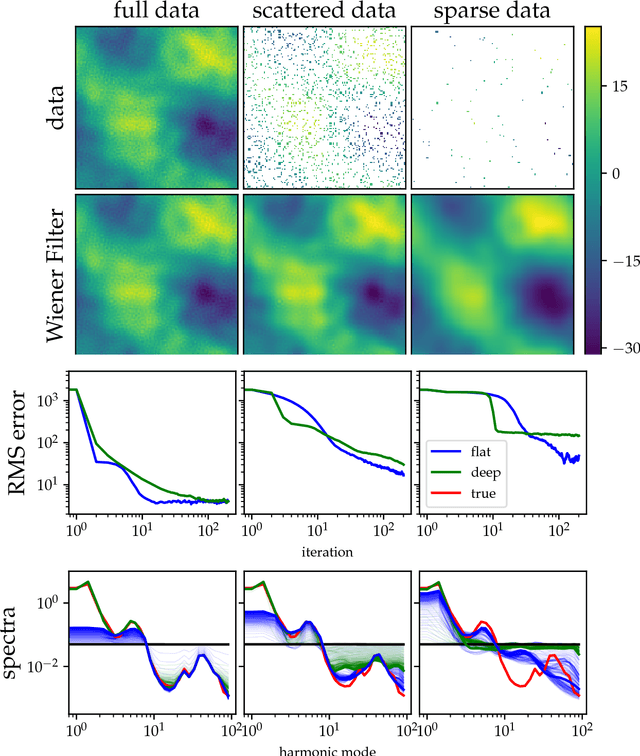
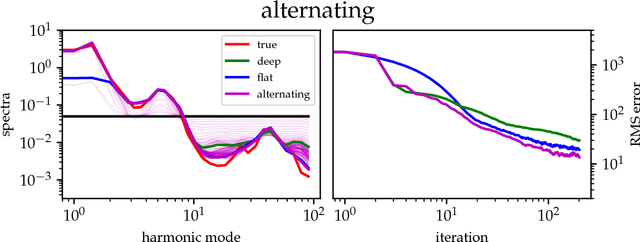
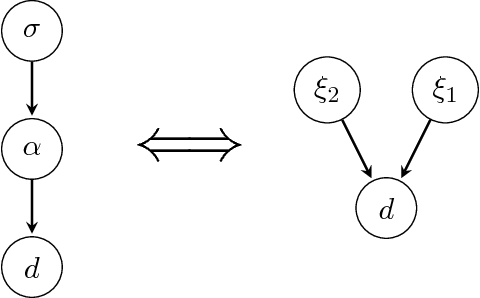
Abstract:The inference of deep hierarchical models is problematic due to strong dependencies between the hierarchies. We investigate a specific transformation of the model parameters based on the multivariate distributional transform. This transformation is a special form of the reparametrization trick, flattens the hierarchy and leads to a standard Gaussian prior on all resulting parameters. The transformation also transfers all the prior information into the structure of the likelihood, hereby decoupling the transformed parameters a priori from each other. A variational Gaussian approximation in this standardized space will be excellent in situations of relatively uninformative data. Additionally, the curvature of the log-posterior is well-conditioned in directions that are weakly constrained by the data, allowing for fast inference in such a scenario. In an example we perform the transformation explicitly for Gaussian process regression with a priori unknown correlation structure. Deep models are inferred rapidly in highly and slowly in poorly informed situations. The flat model show exactly the opposite performance pattern. A synthesis of both, the deep and the flat perspective, provides their combined advantages and overcomes the individual limitations, leading to a faster inference.
Optimal Belief Approximation
Aug 03, 2017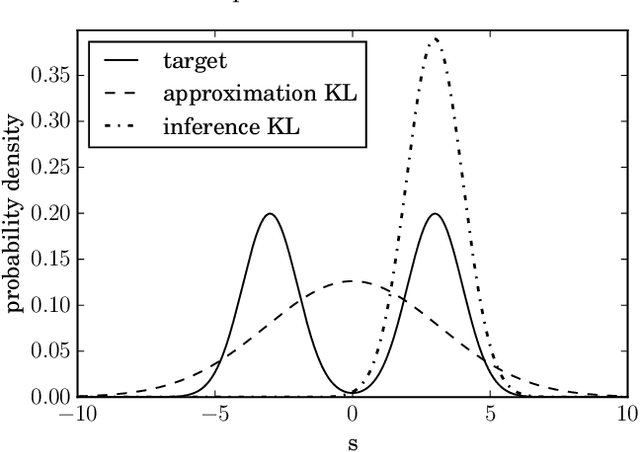
Abstract:In Bayesian statistics probability distributions express beliefs. However, for many problems the beliefs cannot be computed analytically and approximations of beliefs are needed. We seek a loss function that quantifies how "embarrassing" it is to communicate a given approximation. We reproduce and discuss an old proof showing that there is only one ranking under the requirements that (1) the best ranked approximation is the non-approximated belief and (2) that the ranking judges approximations only by their predictions for actual outcomes. The loss function that is obtained in the derivation is equal to the Kullback-Leibler divergence when normalized. This loss function is frequently used in the literature. However, there seems to be confusion about the correct order in which its functional arguments, the approximated and non-approximated beliefs, should be used. The correct order ensures that the recipient of a communication is only deprived of the minimal amount of information. We hope that the elementary derivation settles the apparent confusion. For example when approximating beliefs with Gaussian distributions the optimal approximation is given by moment matching. This is in contrast to many suggested computational schemes.
Correlated signal inference by free energy exploration
Feb 13, 2017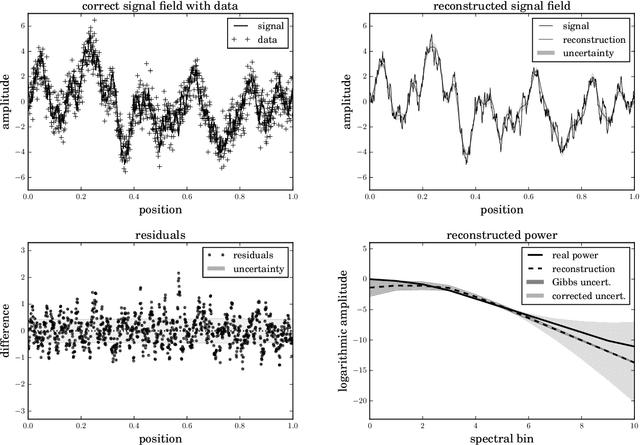
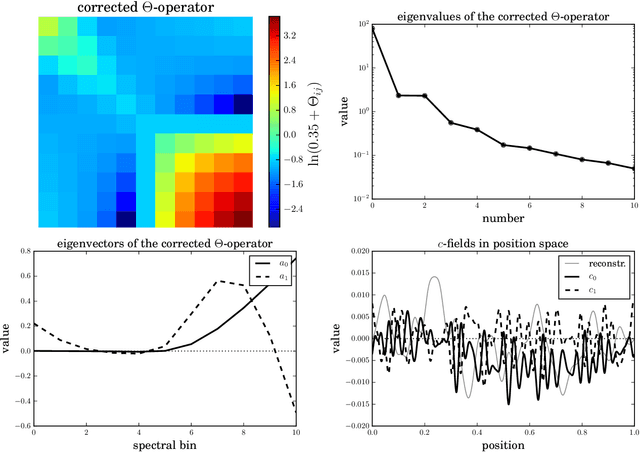
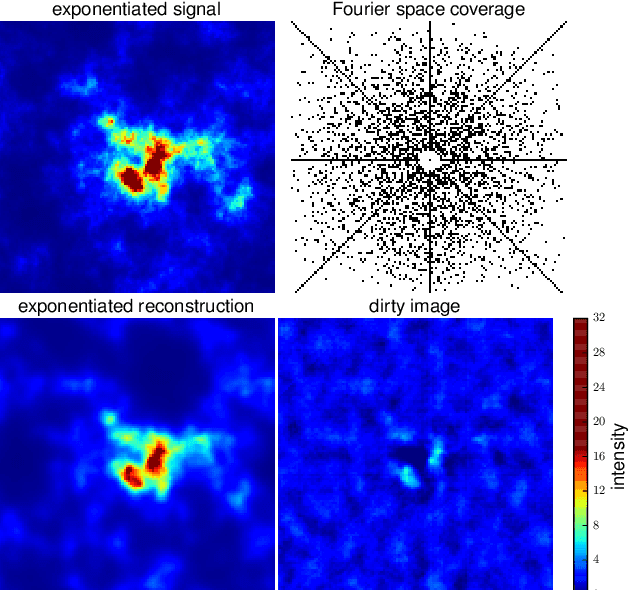
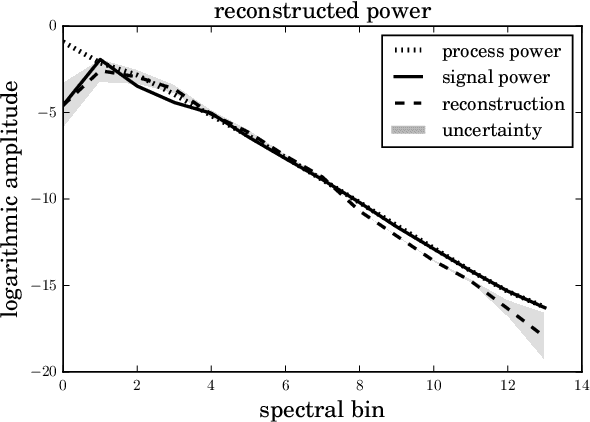
Abstract:The inference of correlated signal fields with unknown correlation structures is of high scientific and technological relevance, but poses significant conceptual and numerical challenges. To address these, we develop the correlated signal inference (CSI) algorithm within information field theory (IFT) and discuss its numerical implementation. To this end, we introduce the free energy exploration (FrEE) strategy for numerical information field theory (NIFTy) applications. The FrEE strategy is to let the mathematical structure of the inference problem determine the dynamics of the numerical solver. FrEE uses the Gibbs free energy formalism for all involved unknown fields and correlation structures without marginalization of nuisance quantities. It thereby avoids the complexity marginalization often impose to IFT equations. FrEE simultaneously solves for the mean and the uncertainties of signal, nuisance, and auxiliary fields, while exploiting any analytically calculable quantity. Finally, FrEE uses a problem specific and self-tuning exploration strategy to swiftly identify the optimal field estimates as well as their uncertainty maps. For all estimated fields, properly weighted posterior samples drawn from their exact, fully non-Gaussian distributions can be generated. Here, we develop the FrEE strategies for the CSI of a normal, a log-normal, and a Poisson log-normal IFT signal inference problem and demonstrate their performances via their NIFTy implementations.
Signal inference with unknown response: Calibration-uncertainty renormalized estimator
Mar 02, 2015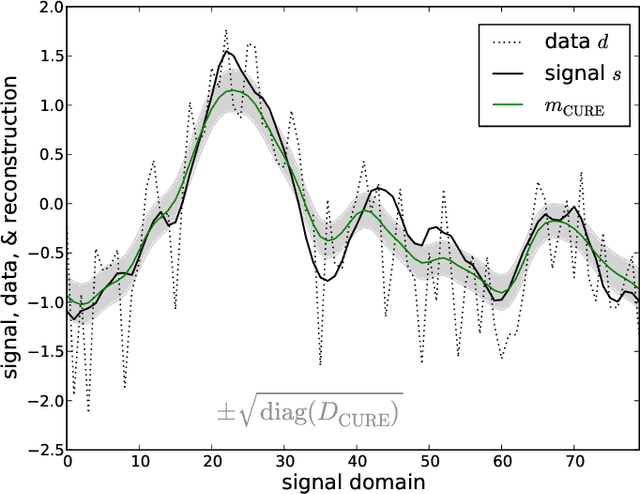
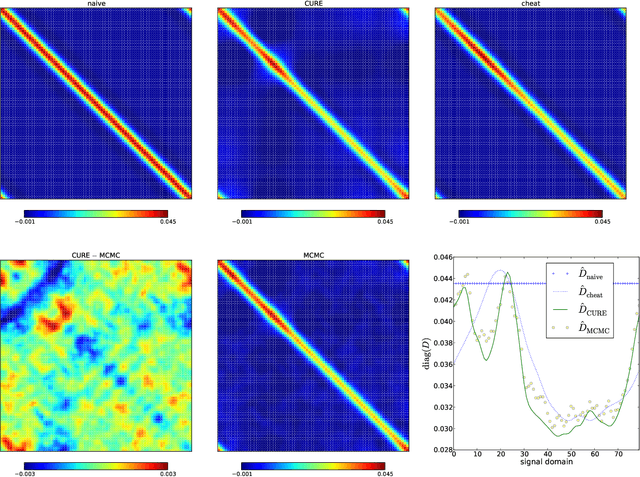
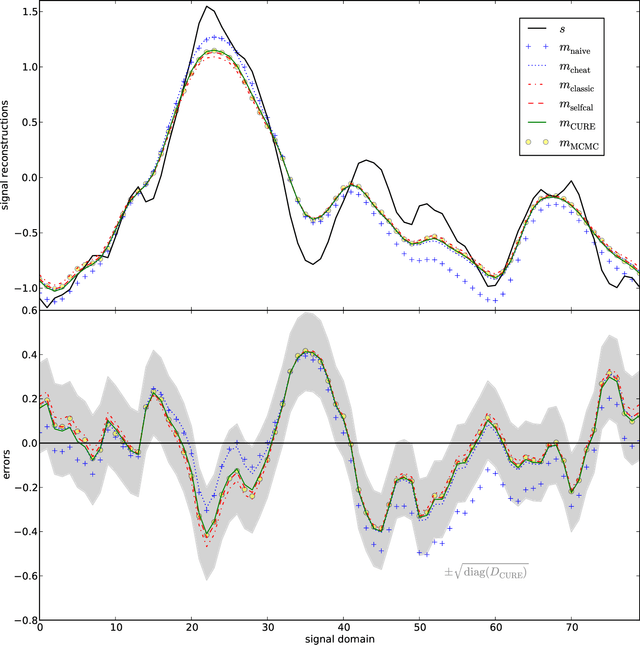
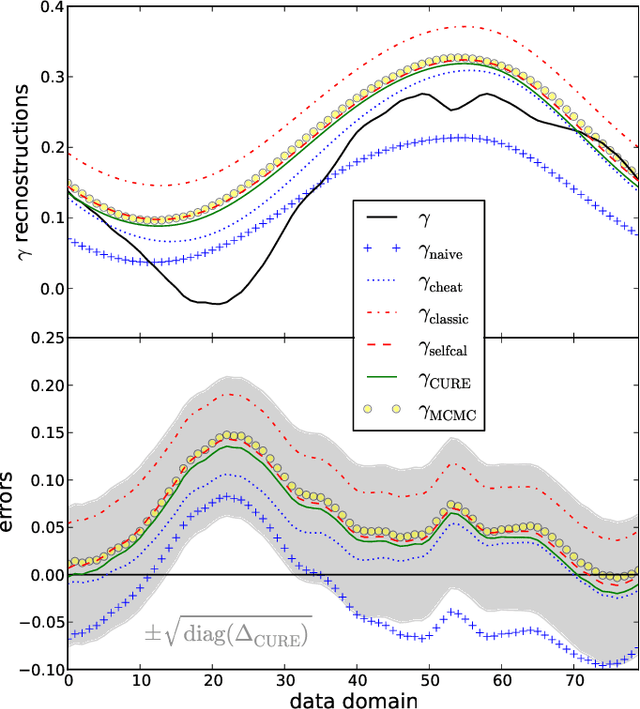
Abstract:The calibration of a measurement device is crucial for every scientific experiment, where a signal has to be inferred from data. We present CURE, the calibration uncertainty renormalized estimator, to reconstruct a signal and simultaneously the instrument's calibration from the same data without knowing the exact calibration, but its covariance structure. The idea of CURE, developed in the framework of information field theory, is starting with an assumed calibration to successively include more and more portions of calibration uncertainty into the signal inference equations and to absorb the resulting corrections into renormalized signal (and calibration) solutions. Thereby, the signal inference and calibration problem turns into solving a single system of ordinary differential equations and can be identified with common resummation techniques used in field theories. We verify CURE by applying it to a simplistic toy example and compare it against existent self-calibration schemes, Wiener filter solutions, and Markov Chain Monte Carlo sampling. We conclude that the method is able to keep up in accuracy with the best self-calibration methods and serves as a non-iterative alternative to it.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge