Maksim Greiner
Signal inference with unknown response: Calibration-uncertainty renormalized estimator
Mar 02, 2015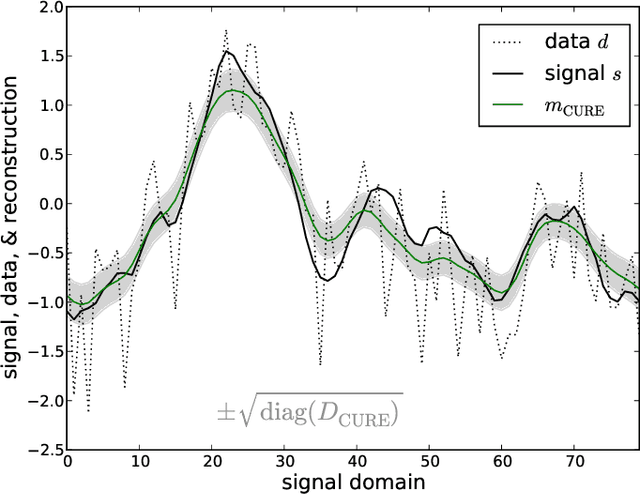
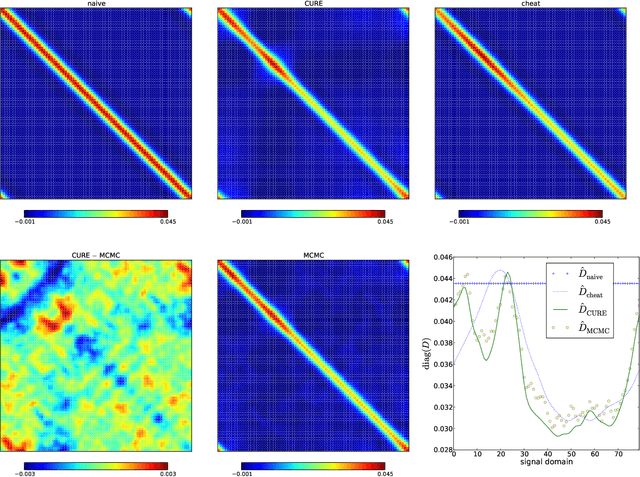
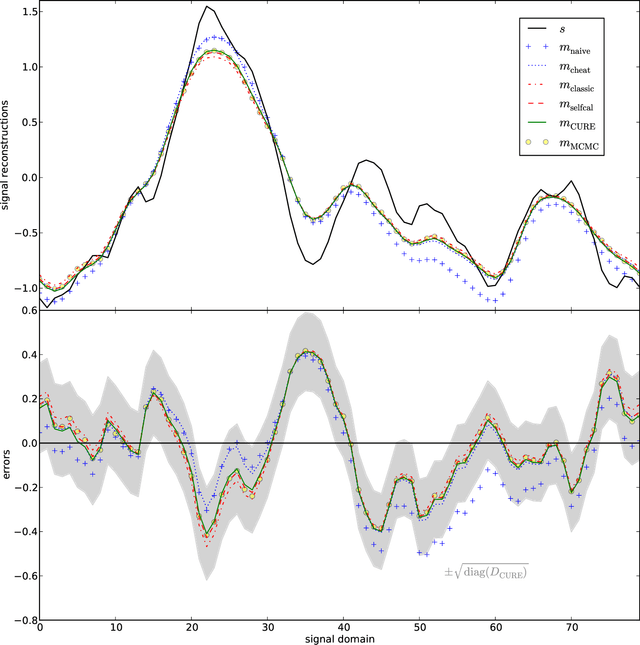
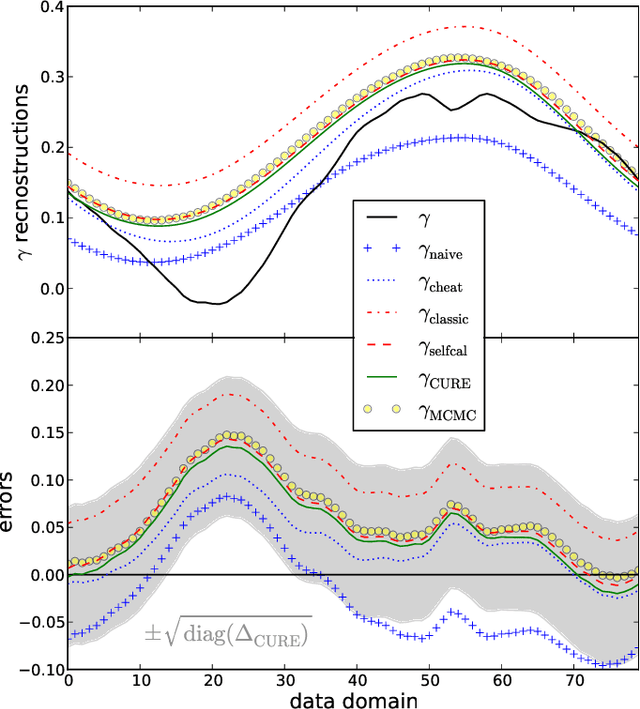
Abstract:The calibration of a measurement device is crucial for every scientific experiment, where a signal has to be inferred from data. We present CURE, the calibration uncertainty renormalized estimator, to reconstruct a signal and simultaneously the instrument's calibration from the same data without knowing the exact calibration, but its covariance structure. The idea of CURE, developed in the framework of information field theory, is starting with an assumed calibration to successively include more and more portions of calibration uncertainty into the signal inference equations and to absorb the resulting corrections into renormalized signal (and calibration) solutions. Thereby, the signal inference and calibration problem turns into solving a single system of ordinary differential equations and can be identified with common resummation techniques used in field theories. We verify CURE by applying it to a simplistic toy example and compare it against existent self-calibration schemes, Wiener filter solutions, and Markov Chain Monte Carlo sampling. We conclude that the method is able to keep up in accuracy with the best self-calibration methods and serves as a non-iterative alternative to it.
Improving self-calibration
Sep 06, 2014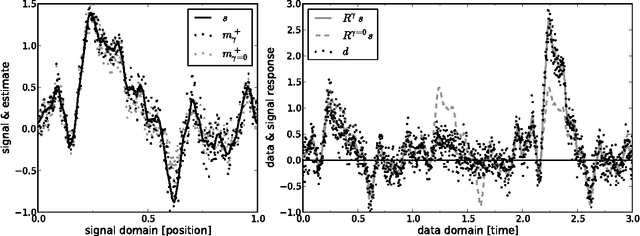
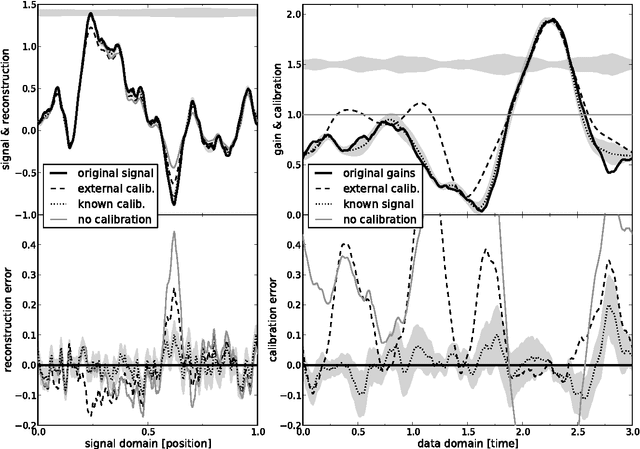
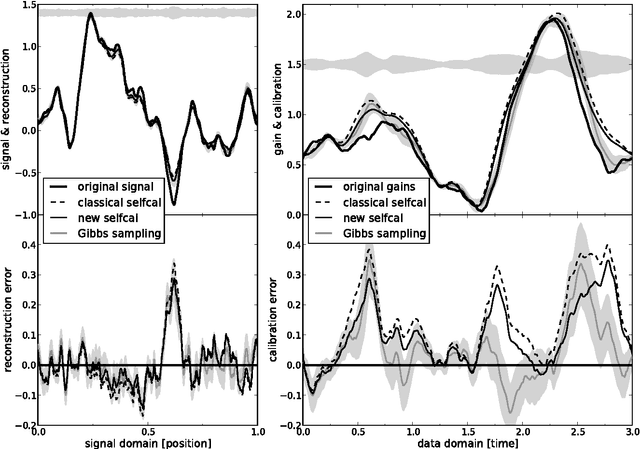
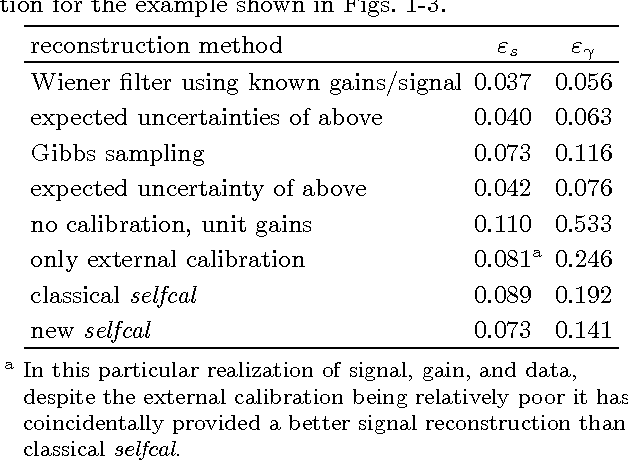
Abstract:Response calibration is the process of inferring how much the measured data depend on the signal one is interested in. It is essential for any quantitative signal estimation on the basis of the data. Here, we investigate self-calibration methods for linear signal measurements and linear dependence of the response on the calibration parameters. The common practice is to augment an external calibration solution using a known reference signal with an internal calibration on the unknown measurement signal itself. Contemporary self-calibration schemes try to find a self-consistent solution for signal and calibration by exploiting redundancies in the measurements. This can be understood in terms of maximizing the joint probability of signal and calibration. However, the full uncertainty structure of this joint probability around its maximum is thereby not taken into account by these schemes. Therefore better schemes -- in sense of minimal square error -- can be designed by accounting for asymmetries in the uncertainty of signal and calibration. We argue that at least a systematic correction of the common self-calibration scheme should be applied in many measurement situations in order to properly treat uncertainties of the signal on which one calibrates. Otherwise the calibration solutions suffer from a systematic bias, which consequently distorts the signal reconstruction. Furthermore, we argue that non-parametric, signal-to-noise filtered calibration should provide more accurate reconstructions than the common bin averages and provide a new, improved self-calibration scheme. We illustrate our findings with a simplistic numerical example.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge