Re-Envisioning Numerical Information Field Theory (NIFTy.re): A Library for Gaussian Processes and Variational Inference

Imaging is the process of transforming noisy, incomplete data into a space that humans can interpret. NIFTy is a Bayesian framework for imaging and has already successfully been applied to many fields in astrophysics. Previous design decisions held the performance and the development of methods in NIFTy back. We present a rewrite of NIFTy, coined NIFTy.re, which reworks the modeling principle, extends the inference strategies, and outsources much of the heavy lifting to JAX. The rewrite dramatically accelerates models written in NIFTy, lays the foundation for new types of inference machineries, improves maintainability, and enables interoperability between NIFTy and the JAX machine learning ecosystem.

Sparse Kernel Gaussian Processes through Iterative Charted Refinement (ICR)

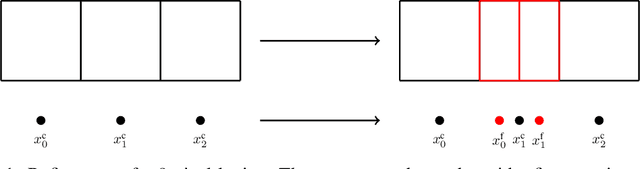
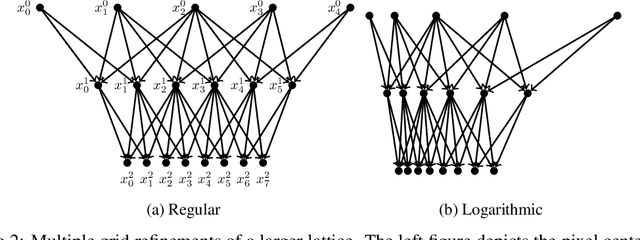
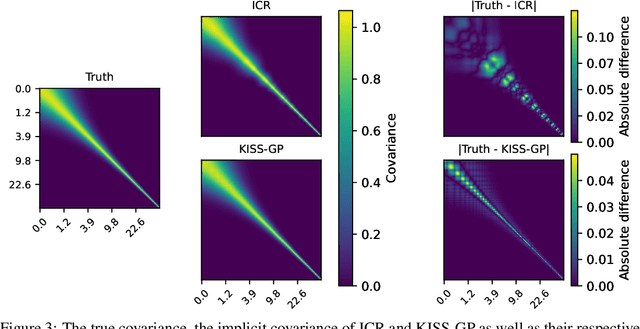
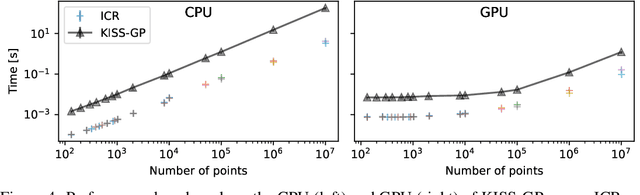
Gaussian Processes (GPs) are highly expressive, probabilistic models. A major limitation is their computational complexity. Naively, exact GP inference requires $\mathcal{O}(N^3)$ computations with $N$ denoting the number of modeled points. Current approaches to overcome this limitation either rely on sparse, structured or stochastic representations of data or kernel respectively and usually involve nested optimizations to evaluate a GP. We present a new, generative method named Iterative Charted Refinement (ICR) to model GPs on nearly arbitrarily spaced points in $\mathcal{O}(N)$ time for decaying kernels without nested optimizations. ICR represents long- as well as short-range correlations by combining views of the modeled locations at varying resolutions with a user-provided coordinate chart. In our experiment with points whose spacings vary over two orders of magnitude, ICR's accuracy is comparable to state-of-the-art GP methods. ICR outperforms existing methods in terms of computational speed by one order of magnitude on the CPU and GPU and has already been successfully applied to model a GP with $122$ billion parameters.

Optimal Belief Approximation

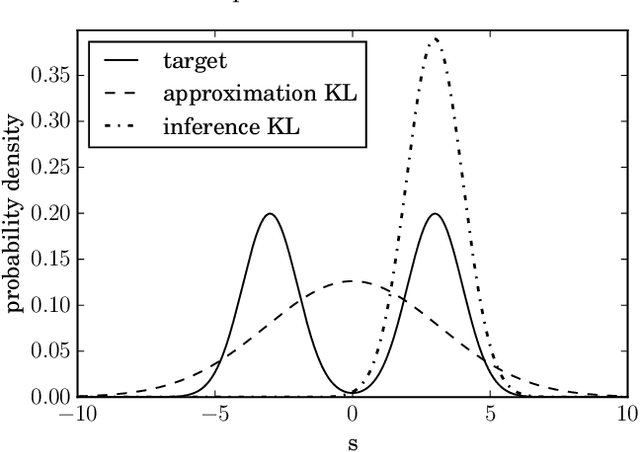
In Bayesian statistics probability distributions express beliefs. However, for many problems the beliefs cannot be computed analytically and approximations of beliefs are needed. We seek a loss function that quantifies how "embarrassing" it is to communicate a given approximation. We reproduce and discuss an old proof showing that there is only one ranking under the requirements that (1) the best ranked approximation is the non-approximated belief and (2) that the ranking judges approximations only by their predictions for actual outcomes. The loss function that is obtained in the derivation is equal to the Kullback-Leibler divergence when normalized. This loss function is frequently used in the literature. However, there seems to be confusion about the correct order in which its functional arguments, the approximated and non-approximated beliefs, should be used. The correct order ensures that the recipient of a communication is only deprived of the minimal amount of information. We hope that the elementary derivation settles the apparent confusion. For example when approximating beliefs with Gaussian distributions the optimal approximation is given by moment matching. This is in contrast to many suggested computational schemes.