Classification and Uncertainty Quantification of Corrupted Data using Semi-Supervised Autoencoders

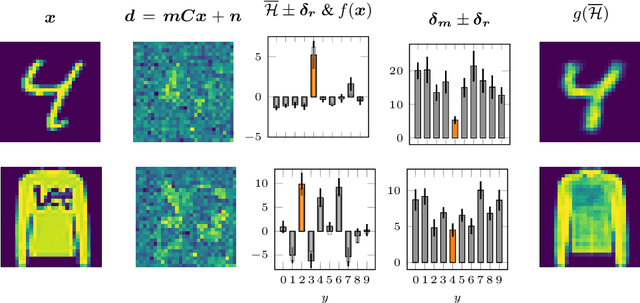
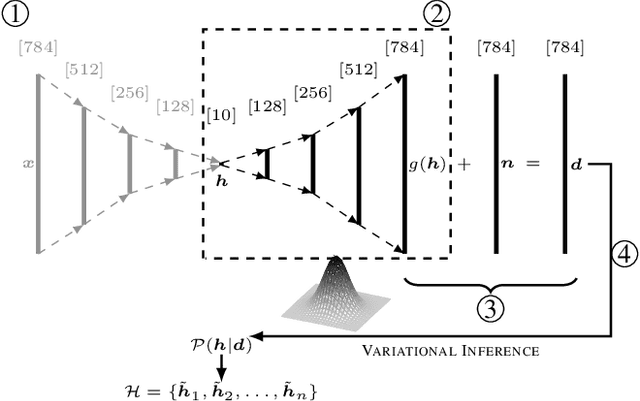
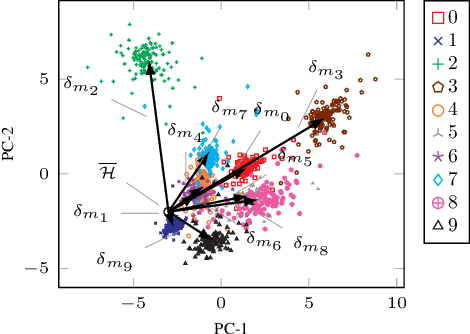
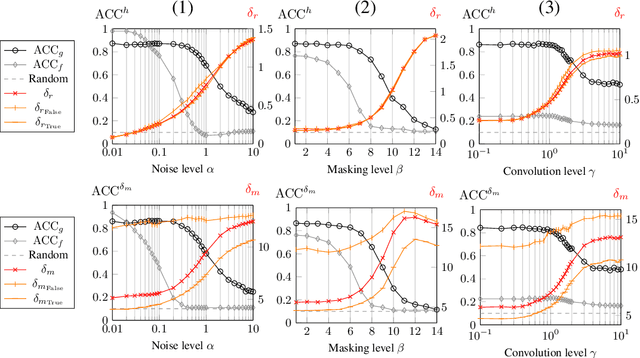
Parametric and non-parametric classifiers often have to deal with real-world data, where corruptions like noise, occlusions, and blur are unavoidable - posing significant challenges. We present a probabilistic approach to classify strongly corrupted data and quantify uncertainty, despite the model only having been trained with uncorrupted data. A semi-supervised autoencoder trained on uncorrupted data is the underlying architecture. We use the decoding part as a generative model for realistic data and extend it by convolutions, masking, and additive Gaussian noise to describe imperfections. This constitutes a statistical inference task in terms of the optimal latent space activations of the underlying uncorrupted datum. We solve this problem approximately with Metric Gaussian Variational Inference (MGVI). The supervision of the autoencoder's latent space allows us to classify corrupted data directly under uncertainty with the statistically inferred latent space activations. Furthermore, we demonstrate that the model uncertainty strongly depends on whether the classification is correct or wrong, setting a basis for a statistical "lie detector" of the classification. Independent of that, we show that the generative model can optimally restore the uncorrupted datum by decoding the inferred latent space activations.

Bayesian Reasoning with Deep-Learned Knowledge

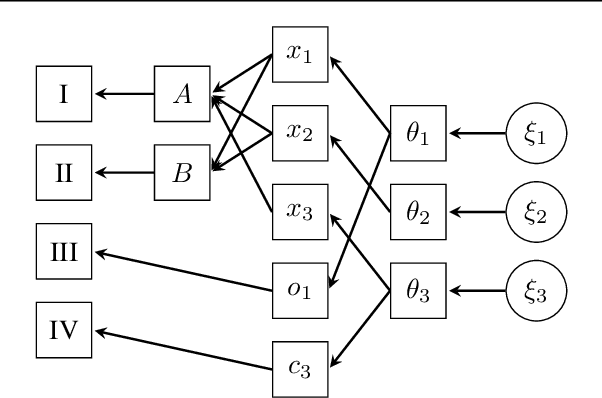
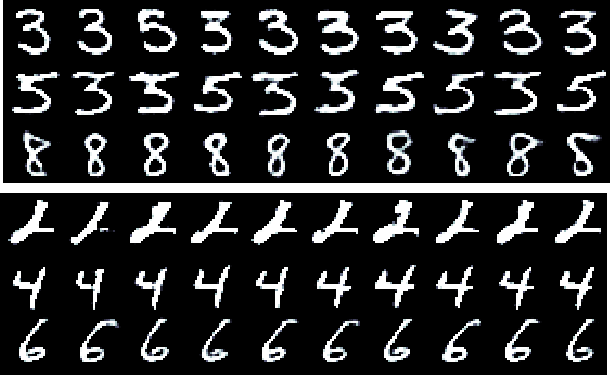
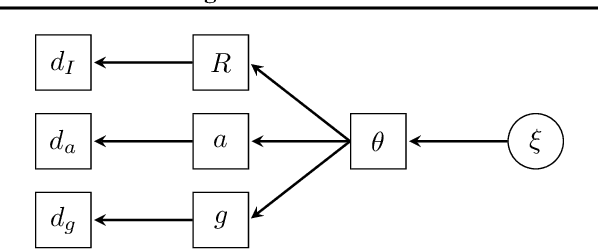
We access the internalized understanding of trained, deep neural networks to perform Bayesian reasoning on complex tasks. Independently trained networks are arranged to jointly answer questions outside their original scope, which are formulated in terms of a Bayesian inference problem. We solve this approximately with variational inference, which provides uncertainty on the outcomes. We demonstrate how following tasks can be approached this way: Combining independently trained networks to sample from a conditional generator, solving riddles involving multiple constraints simultaneously, and combine deep-learned knowledge with conventional noisy measurements in the context of high-resolution images of human faces.

Metric Gaussian Variational Inference

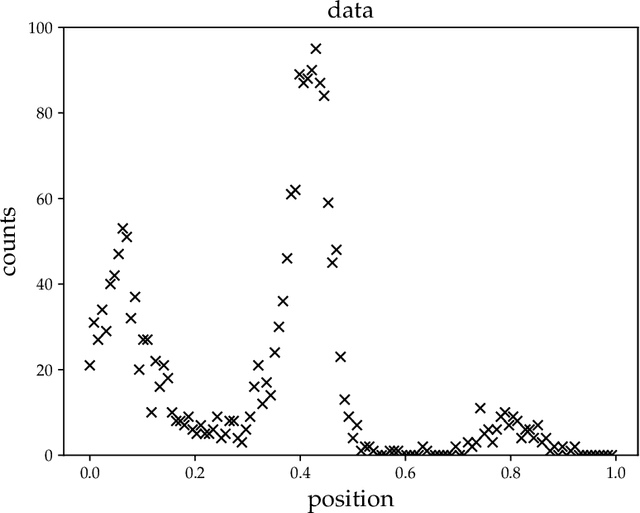
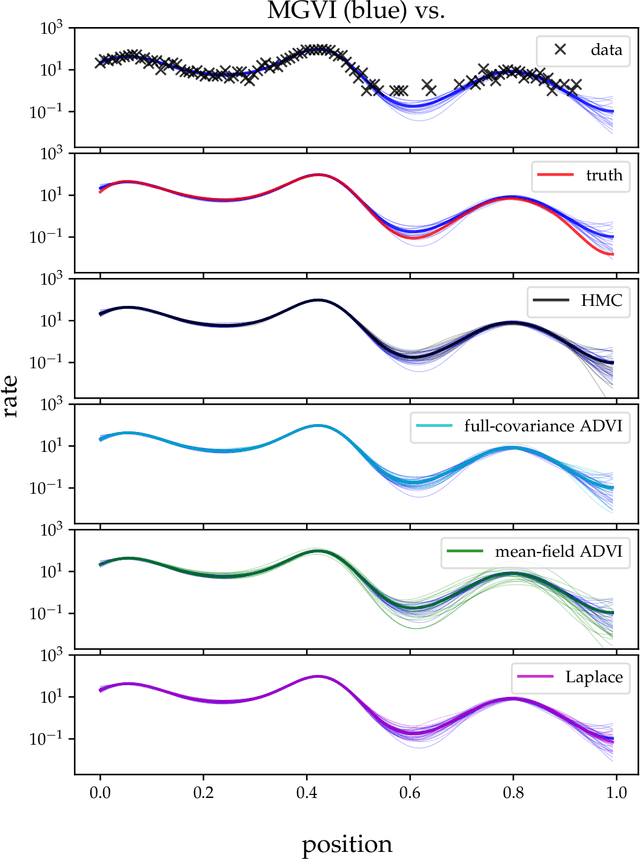
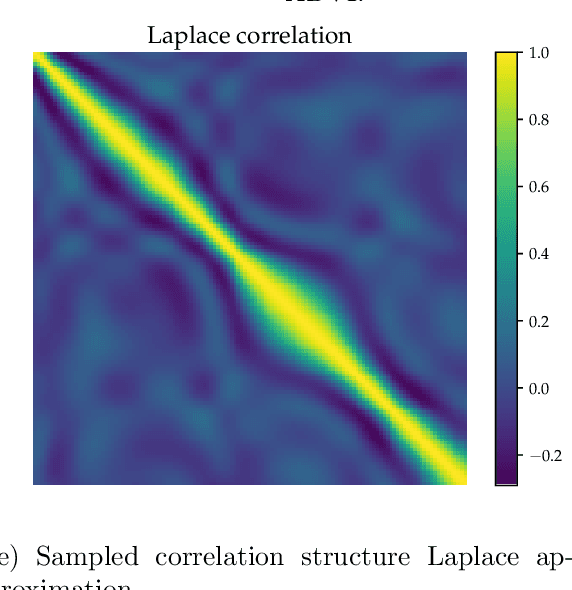
A variational Gaussian approximation of the posterior distribution can be an excellent way to infer posterior quantities. However, to capture all posterior correlations the parametrization of the full covariance is required, which scales quadratic with the problem size. This scaling prohibits full-covariance approximations for large-scale problems. As a solution to this limitation we propose Metric Gaussian Variational Inference (MGVI). This procedure approximates the variational covariance such that it requires no parameters on its own and still provides reliable posterior correlations and uncertainties for all model parameters. We approximate the variational covariance with the inverse Fisher metric, a local estimate of the true posterior uncertainty. This covariance is only stored implicitly and all necessary quantities can be extracted from it by independent samples drawn from the approximating Gaussian. MGVI requires the minimization of a stochastic estimate of the Kullback-Leibler divergence only with respect to the mean of the variational Gaussian, a quantity that only scales linearly with the problem size. We motivate the choice of this covariance from an information geometric perspective. The method is validated against established approaches in a small example and the scaling is demonstrated in a problem with over a million parameters.

Encoding prior knowledge in the structure of the likelihood

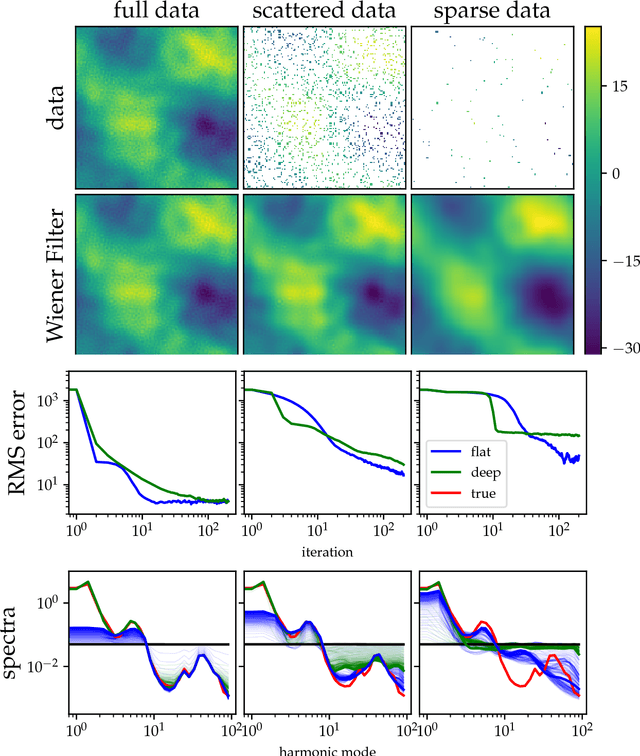
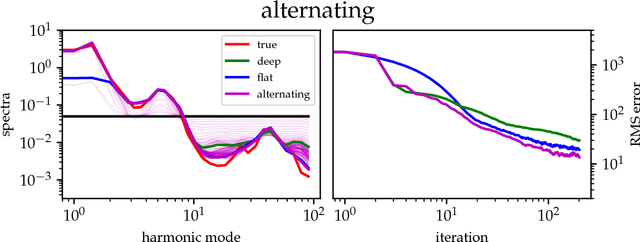
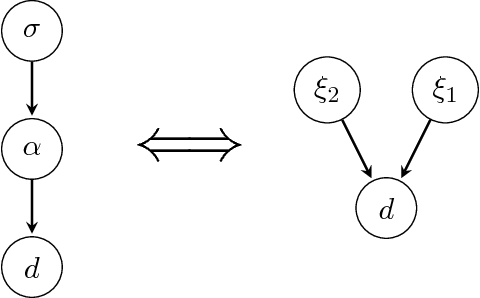
The inference of deep hierarchical models is problematic due to strong dependencies between the hierarchies. We investigate a specific transformation of the model parameters based on the multivariate distributional transform. This transformation is a special form of the reparametrization trick, flattens the hierarchy and leads to a standard Gaussian prior on all resulting parameters. The transformation also transfers all the prior information into the structure of the likelihood, hereby decoupling the transformed parameters a priori from each other. A variational Gaussian approximation in this standardized space will be excellent in situations of relatively uninformative data. Additionally, the curvature of the log-posterior is well-conditioned in directions that are weakly constrained by the data, allowing for fast inference in such a scenario. In an example we perform the transformation explicitly for Gaussian process regression with a priori unknown correlation structure. Deep models are inferred rapidly in highly and slowly in poorly informed situations. The flat model show exactly the opposite performance pattern. A synthesis of both, the deep and the flat perspective, provides their combined advantages and overcomes the individual limitations, leading to a faster inference.

Correlated signal inference by free energy exploration

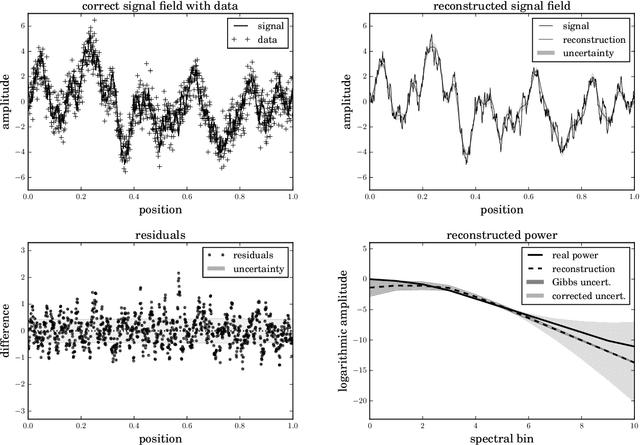
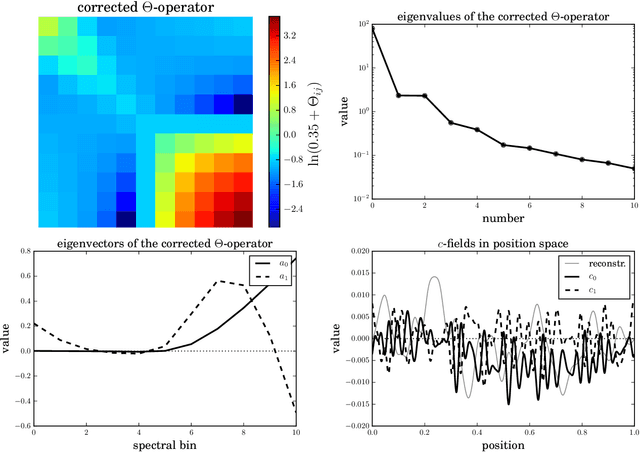
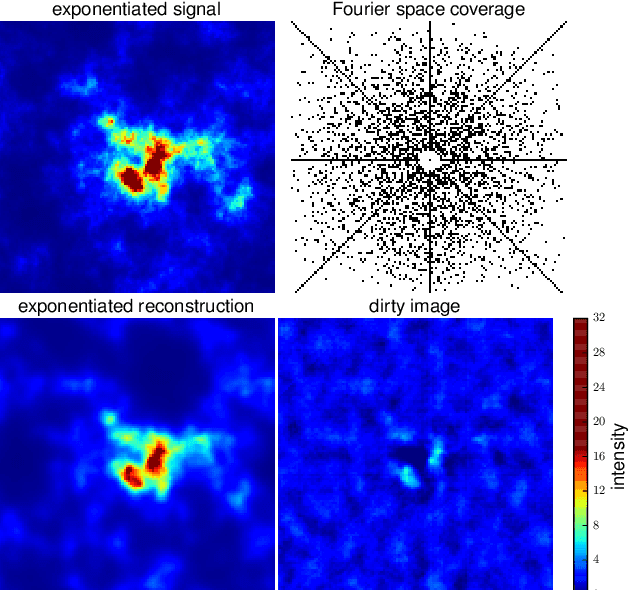
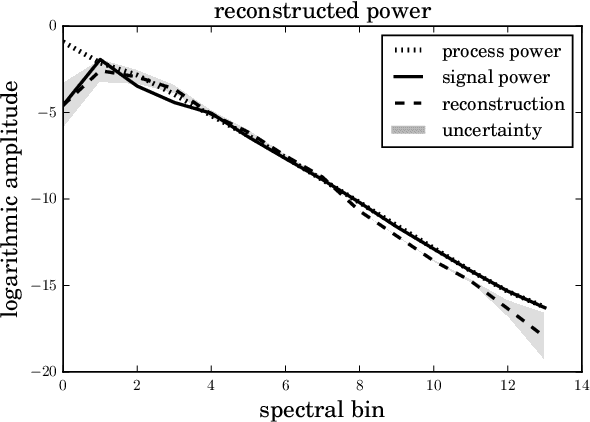
The inference of correlated signal fields with unknown correlation structures is of high scientific and technological relevance, but poses significant conceptual and numerical challenges. To address these, we develop the correlated signal inference (CSI) algorithm within information field theory (IFT) and discuss its numerical implementation. To this end, we introduce the free energy exploration (FrEE) strategy for numerical information field theory (NIFTy) applications. The FrEE strategy is to let the mathematical structure of the inference problem determine the dynamics of the numerical solver. FrEE uses the Gibbs free energy formalism for all involved unknown fields and correlation structures without marginalization of nuisance quantities. It thereby avoids the complexity marginalization often impose to IFT equations. FrEE simultaneously solves for the mean and the uncertainties of signal, nuisance, and auxiliary fields, while exploiting any analytically calculable quantity. Finally, FrEE uses a problem specific and self-tuning exploration strategy to swiftly identify the optimal field estimates as well as their uncertainty maps. For all estimated fields, properly weighted posterior samples drawn from their exact, fully non-Gaussian distributions can be generated. Here, we develop the FrEE strategies for the CSI of a normal, a log-normal, and a Poisson log-normal IFT signal inference problem and demonstrate their performances via their NIFTy implementations.