Deep Stochastic Processes via Functional Markov Transition Operators

We introduce Markov Neural Processes (MNPs), a new class of Stochastic Processes (SPs) which are constructed by stacking sequences of neural parameterised Markov transition operators in function space. We prove that these Markov transition operators can preserve the exchangeability and consistency of SPs. Therefore, the proposed iterative construction adds substantial flexibility and expressivity to the original framework of Neural Processes (NPs) without compromising consistency or adding restrictions. Our experiments demonstrate clear advantages of MNPs over baseline models on a variety of tasks.

Prediction-Oriented Bayesian Active Learning

Information-theoretic approaches to active learning have traditionally focused on maximising the information gathered about the model parameters, most commonly by optimising the BALD score. We highlight that this can be suboptimal from the perspective of predictive performance. For example, BALD lacks a notion of an input distribution and so is prone to prioritise data of limited relevance. To address this we propose the expected predictive information gain (EPIG), an acquisition function that measures information gain in the space of predictions rather than parameters. We find that using EPIG leads to stronger predictive performance compared with BALD across a range of datasets and models, and thus provides an appealing drop-in replacement.

Incorporating Unlabelled Data into Bayesian Neural Networks

We develop a contrastive framework for learning better prior distributions for Bayesian Neural Networks (BNNs) using unlabelled data. With this framework, we propose a practical BNN algorithm that offers the label-efficiency of self-supervised learning and the principled uncertainty estimates of Bayesian methods. Finally, we demonstrate the advantages of our approach for data-efficient learning in semi-supervised and low-budget active learning problems.

Modern Bayesian Experimental Design

Bayesian experimental design (BED) provides a powerful and general framework for optimizing the design of experiments. However, its deployment often poses substantial computational challenges that can undermine its practical use. In this review, we outline how recent advances have transformed our ability to overcome these challenges and thus utilize BED effectively, before discussing some key areas for future development in the field.

CO-BED: Information-Theoretic Contextual Optimization via Bayesian Experimental Design

We formalize the problem of contextual optimization through the lens of Bayesian experimental design and propose CO-BED -- a general, model-agnostic framework for designing contextual experiments using information-theoretic principles. After formulating a suitable information-based objective, we employ black-box variational methods to simultaneously estimate it and optimize the designs in a single stochastic gradient scheme. We further introduce a relaxation scheme to allow discrete actions to be accommodated. As a result, CO-BED provides a general and automated solution to a wide range of contextual optimization problems. We illustrate its effectiveness in a number of experiments, where CO-BED demonstrates competitive performance even when compared to bespoke, model-specific alternatives.

Do Bayesian Neural Networks Need To Be Fully Stochastic?

We investigate the efficacy of treating all the parameters in a Bayesian neural network stochastically and find compelling theoretical and empirical evidence that this standard construction may be unnecessary. To this end, we prove that expressive predictive distributions require only small amounts of stochasticity. In particular, partially stochastic networks with only $n$ stochastic biases are universal probabilistic predictors for $n$-dimensional predictive problems. In empirical investigations, we find no systematic benefit of full stochasticity across four different inference modalities and eight datasets; partially stochastic networks can match and sometimes even outperform fully stochastic networks, despite their reduced memory costs.

Learning Instance-Specific Data Augmentations

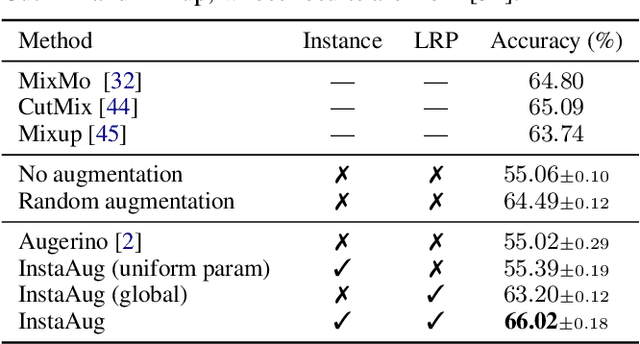
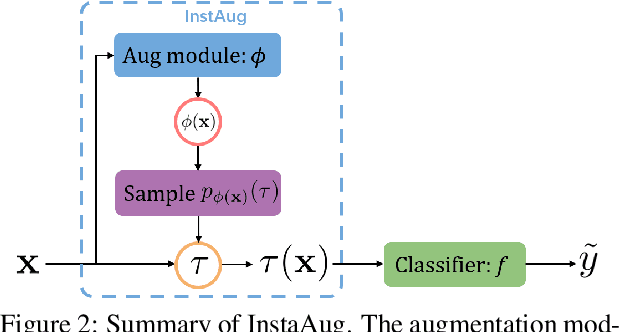
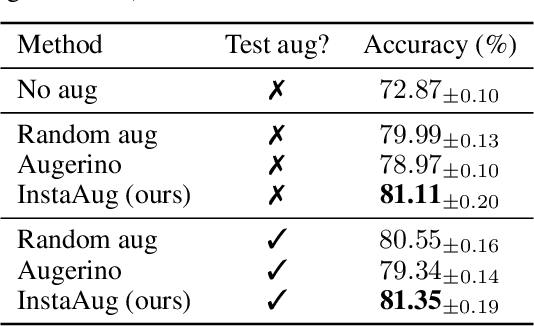
Existing data augmentation methods typically assume independence between transformations and inputs: they use the same transformation distribution for all input instances. We explain why this can be problematic and propose InstaAug, a method for automatically learning input-specific augmentations from data. This is achieved by introducing an augmentation module that maps an input to a distribution over transformations. This is simultaneously trained alongside the base model in a fully end-to-end manner using only the training data. We empirically demonstrate that InstaAug learns meaningful augmentations for a wide range of transformation classes, which in turn provides better performance on supervised and self-supervised tasks compared with augmentations that assume input--transformation independence.

A Continuous Time Framework for Discrete Denoising Models

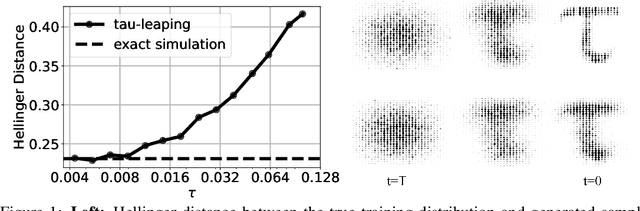
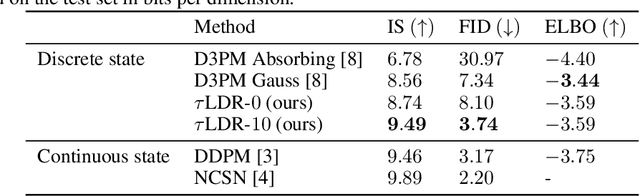
We provide the first complete continuous time framework for denoising diffusion models of discrete data. This is achieved by formulating the forward noising process and corresponding reverse time generative process as Continuous Time Markov Chains (CTMCs). The model can be efficiently trained using a continuous time version of the ELBO. We simulate the high dimensional CTMC using techniques developed in chemical physics and exploit our continuous time framework to derive high performance samplers that we show can outperform discrete time methods for discrete data. The continuous time treatment also enables us to derive a novel theoretical result bounding the error between the generated sample distribution and the true data distribution.

Active Surrogate Estimators: An Active Learning Approach to Label-Efficient Model Evaluation

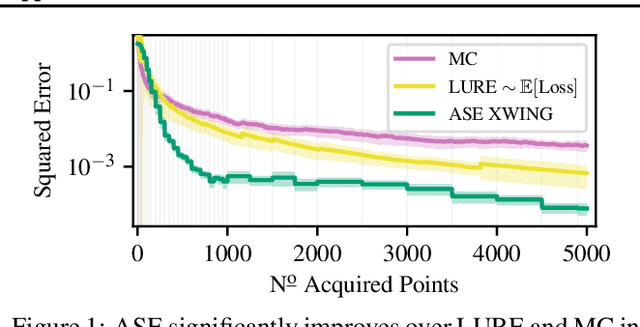
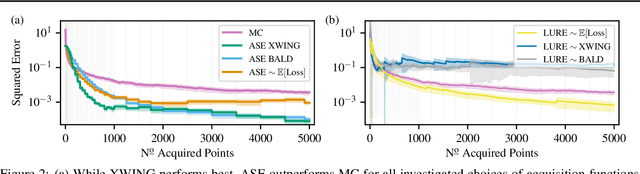
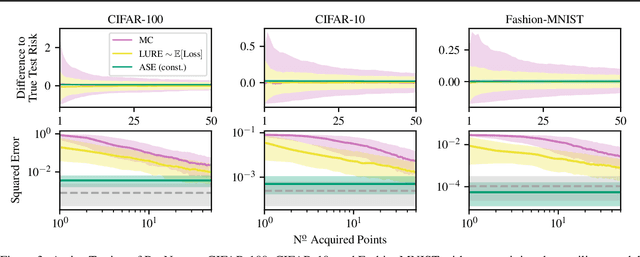
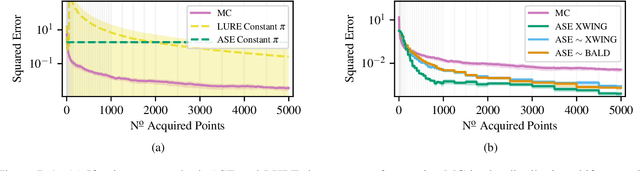
We propose Active Surrogate Estimators (ASEs), a new method for label-efficient model evaluation. Evaluating model performance is a challenging and important problem when labels are expensive. ASEs address this active testing problem using a surrogate-based estimation approach, whereas previous methods have focused on Monte Carlo estimates. ASEs actively learn the underlying surrogate, and we propose a novel acquisition strategy, XWING, that tailors this learning to the final estimation task. We find that ASEs offer greater label-efficiency than the current state-of-the-art when applied to challenging model evaluation problems for deep neural networks. We further theoretically analyze ASEs' errors.

Implicit Deep Adaptive Design: Policy-Based Experimental Design without Likelihoods

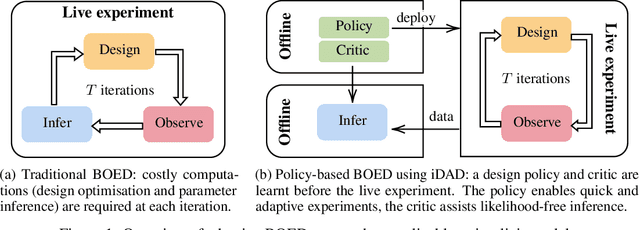
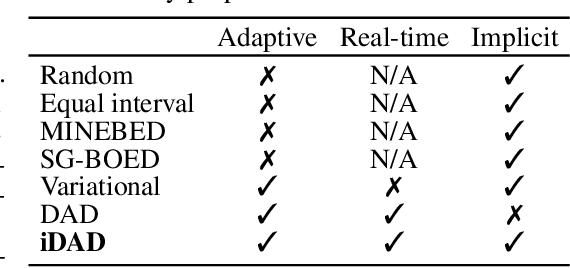
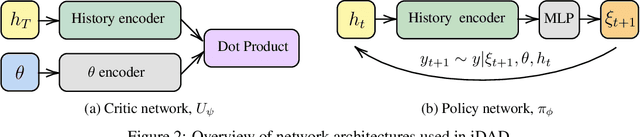
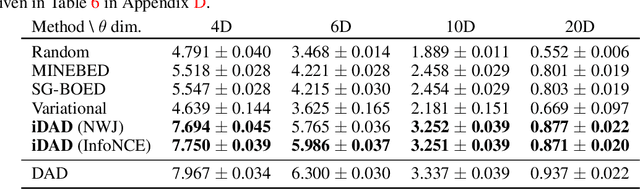
We introduce implicit Deep Adaptive Design (iDAD), a new method for performing adaptive experiments in real-time with implicit models. iDAD amortizes the cost of Bayesian optimal experimental design (BOED) by learning a design policy network upfront, which can then be deployed quickly at the time of the experiment. The iDAD network can be trained on any model which simulates differentiable samples, unlike previous design policy work that requires a closed form likelihood and conditionally independent experiments. At deployment, iDAD allows design decisions to be made in milliseconds, in contrast to traditional BOED approaches that require heavy computation during the experiment itself. We illustrate the applicability of iDAD on a number of experiments, and show that it provides a fast and effective mechanism for performing adaptive design with implicit models.