Michael U. Gutmann
CFMI: Flow Matching for Missing Data Imputation
Jun 10, 2025Abstract:We introduce conditional flow matching for imputation (CFMI), a new general-purpose method to impute missing data. The method combines continuous normalising flows, flow-matching, and shared conditional modelling to deal with intractabilities of traditional multiple imputation. Our comparison with nine classical and state-of-the-art imputation methods on 24 small to moderate-dimensional tabular data sets shows that CFMI matches or outperforms both traditional and modern techniques across a wide range of metrics. Applying the method to zero-shot imputation of time-series data, we find that it matches the accuracy of a related diffusion-based method while outperforming it in terms of computational efficiency. Overall, CFMI performs at least as well as traditional methods on lower-dimensional data while remaining scalable to high-dimensional settings, matching or exceeding the performance of other deep learning-based approaches, making it a go-to imputation method for a wide range of data types and dimensionalities.
Simulation-based Bayesian inference under model misspecification
Mar 16, 2025Abstract:Simulation-based Bayesian inference (SBI) methods are widely used for parameter estimation in complex models where evaluating the likelihood is challenging but generating simulations is relatively straightforward. However, these methods commonly assume that the simulation model accurately reflects the true data-generating process, an assumption that is frequently violated in realistic scenarios. In this paper, we focus on the challenges faced by SBI methods under model misspecification. We consolidate recent research aimed at mitigating the effects of misspecification, highlighting three key strategies: i) robust summary statistics, ii) generalised Bayesian inference, and iii) error modelling and adjustment parameters. To illustrate both the vulnerabilities of popular SBI methods and the effectiveness of misspecification-robust alternatives, we present empirical results on an illustrative example.
Improving Variational Autoencoder Estimation from Incomplete Data with Mixture Variational Families
Mar 05, 2024Abstract:We consider the task of estimating variational autoencoders (VAEs) when the training data is incomplete. We show that missing data increases the complexity of the model's posterior distribution over the latent variables compared to the fully-observed case. The increased complexity may adversely affect the fit of the model due to a mismatch between the variational and model posterior distributions. We introduce two strategies based on (i) finite variational-mixture and (ii) imputation-based variational-mixture distributions to address the increased posterior complexity. Through a comprehensive evaluation of the proposed approaches, we show that variational mixtures are effective at improving the accuracy of VAE estimation from incomplete data.
Conditional Sampling of Variational Autoencoders via Iterated Approximate Ancestral Sampling
Aug 17, 2023Abstract:Conditional sampling of variational autoencoders (VAEs) is needed in various applications, such as missing data imputation, but is computationally intractable. A principled choice for asymptotically exact conditional sampling is Metropolis-within-Gibbs (MWG). However, we observe that the tendency of VAEs to learn a structured latent space, a commonly desired property, can cause the MWG sampler to get "stuck" far from the target distribution. This paper mitigates the limitations of MWG: we systematically outline the pitfalls in the context of VAEs, propose two original methods that address these pitfalls, and demonstrate an improved performance of the proposed methods on a set of sampling tasks.
Designing Optimal Behavioral Experiments Using Machine Learning
May 12, 2023



Abstract:Computational models are powerful tools for understanding human cognition and behavior. They let us express our theories clearly and precisely, and offer predictions that can be subtle and often counter-intuitive. However, this same richness and ability to surprise means our scientific intuitions and traditional tools are ill-suited to designing experiments to test and compare these models. To avoid these pitfalls and realize the full potential of computational modeling, we require tools to design experiments that provide clear answers about what models explain human behavior and the auxiliary assumptions those models must make. Bayesian optimal experimental design (BOED) formalizes the search for optimal experimental designs by identifying experiments that are expected to yield informative data. In this work, we provide a tutorial on leveraging recent advances in BOED and machine learning to find optimal experiments for any kind of model that we can simulate data from, and show how by-products of this procedure allow for quick and straightforward evaluation of models and their parameters against real experimental data. As a case study, we consider theories of how people balance exploration and exploitation in multi-armed bandit decision-making tasks. We validate the presented approach using simulations and a real-world experiment. As compared to experimental designs commonly used in the literature, we show that our optimal designs more efficiently determine which of a set of models best account for individual human behavior, and more efficiently characterize behavior given a preferred model. We provide code to replicate all analyses as well as tutorial notebooks and pointers to adapt the methodology to other experimental settings.
Estimating the Density Ratio between Distributions with High Discrepancy using Multinomial Logistic Regression
May 01, 2023



Abstract:Functions of the ratio of the densities $p/q$ are widely used in machine learning to quantify the discrepancy between the two distributions $p$ and $q$. For high-dimensional distributions, binary classification-based density ratio estimators have shown great promise. However, when densities are well separated, estimating the density ratio with a binary classifier is challenging. In this work, we show that the state-of-the-art density ratio estimators perform poorly on well-separated cases and demonstrate that this is due to distribution shifts between training and evaluation time. We present an alternative method that leverages multi-class classification for density ratio estimation and does not suffer from distribution shift issues. The method uses a set of auxiliary densities $\{m_k\}_{k=1}^K$ and trains a multi-class logistic regression to classify the samples from $p, q$, and $\{m_k\}_{k=1}^K$ into $K+2$ classes. We show that if these auxiliary densities are constructed such that they overlap with $p$ and $q$, then a multi-class logistic regression allows for estimating $\log p/q$ on the domain of any of the $K+2$ distributions and resolves the distribution shift problems of the current state-of-the-art methods. We compare our method to state-of-the-art density ratio estimators on both synthetic and real datasets and demonstrate its superior performance on the tasks of density ratio estimation, mutual information estimation, and representation learning. Code: https://www.blackswhan.com/mdre/
Bayesian Optimization with Informative Covariance
Aug 04, 2022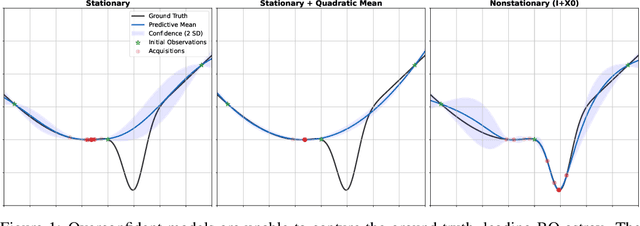
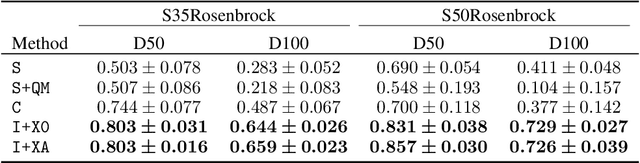
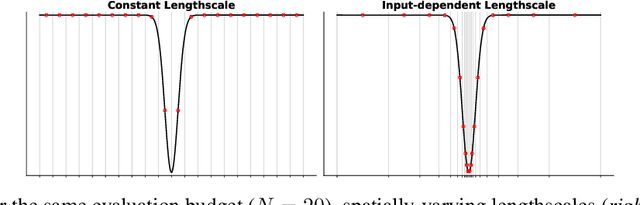

Abstract:Bayesian Optimization is a methodology for global optimization of unknown and expensive objectives. It combines a surrogate Bayesian regression model with an acquisition function to decide where to evaluate the objective. Typical regression models are Gaussian processes with stationary covariance functions, which, however, are unable to express prior input-dependent information, in particular information about possible locations of the optimum. The ubiquity of stationary models has led to the common practice of exploiting prior information via informative mean functions. In this paper, we highlight that these models can lead to poor performance, especially in high dimensions. We propose novel informative covariance functions that leverage nonstationarity to encode preferences for certain regions of the search space and adaptively promote local exploration during the optimization. We demonstrate that they can increase the sample efficiency of the optimization in high dimensions, even under weak prior information.
Pen and Paper Exercises in Machine Learning
Jun 27, 2022



Abstract:This is a collection of (mostly) pen-and-paper exercises in machine learning. The exercises are on the following topics: linear algebra, optimisation, directed graphical models, undirected graphical models, expressive power of graphical models, factor graphs and message passing, inference for hidden Markov models, model-based learning (including ICA and unnormalised models), sampling and Monte-Carlo integration, and variational inference.
Statistical applications of contrastive learning
Apr 29, 2022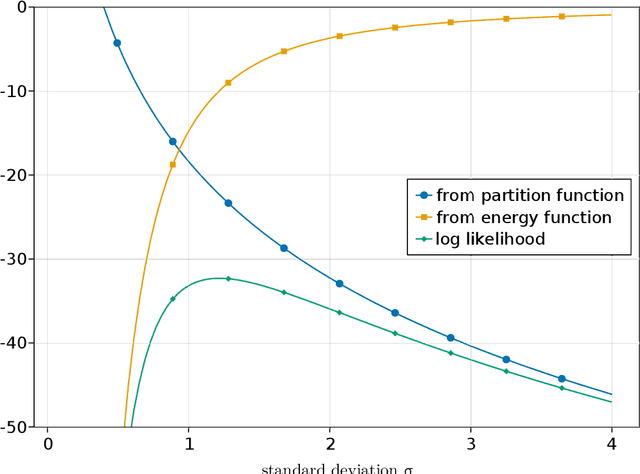
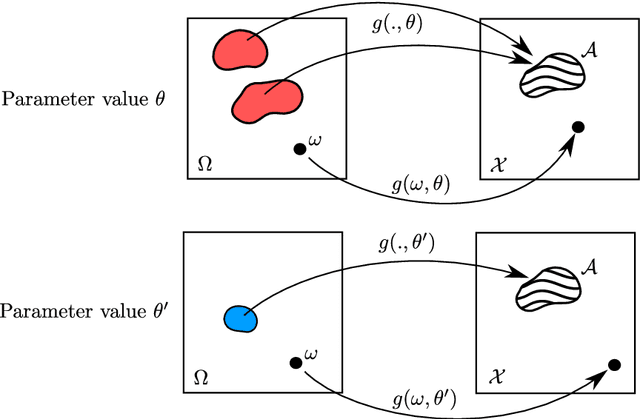
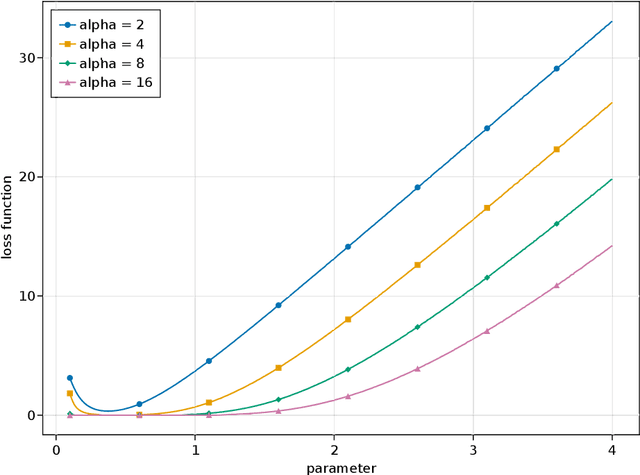
Abstract:The likelihood function plays a crucial role in statistical inference and experimental design. However, it is computationally intractable for several important classes of statistical models, including energy-based models and simulator-based models. Contrastive learning is an intuitive and computationally feasible alternative to likelihood-based learning. We here first provide an introduction to contrastive learning and then show how we can use it to derive methods for diverse statistical problems, namely parameter estimation for energy-based models, Bayesian inference for simulator-based models, as well as experimental design.
Variational Gibbs inference for statistical model estimation from incomplete data
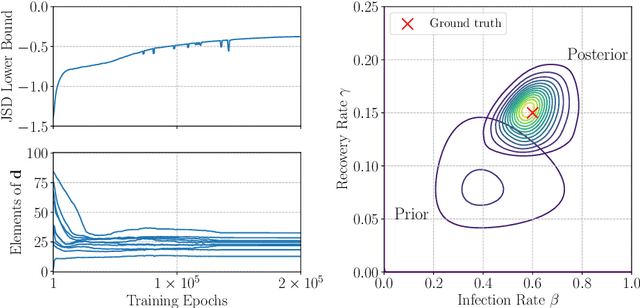
Nov 25, 2021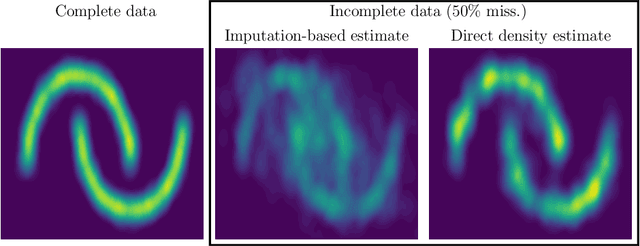

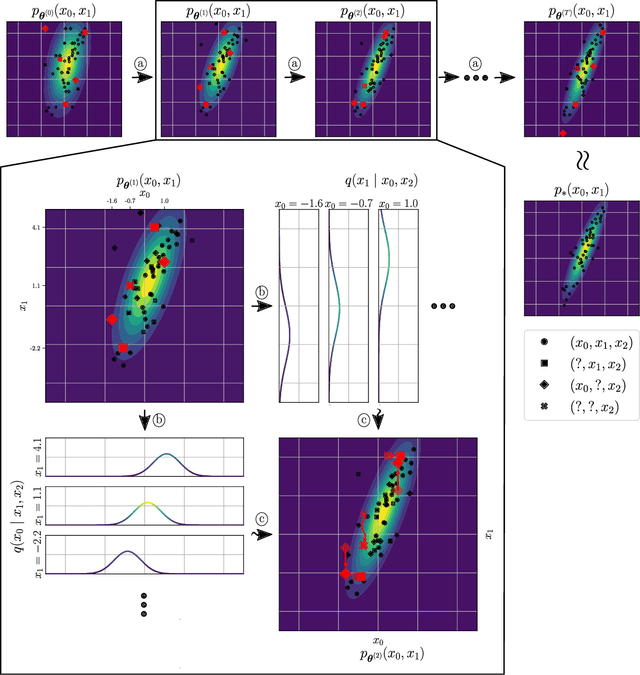
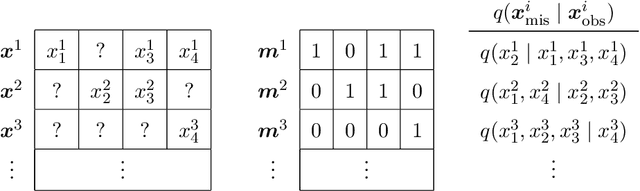
Abstract:Statistical models are central to machine learning with broad applicability across a range of downstream tasks. The models are typically controlled by free parameters that are estimated from data by maximum-likelihood estimation. However, when faced with real-world datasets many of the models run into a critical issue: they are formulated in terms of fully-observed data, whereas in practice the datasets are plagued with missing data. The theory of statistical model estimation from incomplete data is conceptually similar to the estimation of latent-variable models, where powerful tools such as variational inference (VI) exist. However, in contrast to standard latent-variable models, parameter estimation with incomplete data often requires estimating exponentially-many conditional distributions of the missing variables, hence making standard VI methods intractable. We address this gap by introducing variational Gibbs inference (VGI), a new general-purpose method to estimate the parameters of statistical models from incomplete data. We validate VGI on a set of synthetic and real-world estimation tasks, estimating important machine learning models, VAEs and normalising flows, from incomplete data. The proposed method, whilst general-purpose, achieves competitive or better performance than existing model-specific estimation methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge