Metrics for Parametric Families of Networks

We introduce a general framework for analyzing data modeled as parameterized families of networks. Building on a Gromov-Wasserstein variant of optimal transport, we define a family of parameterized Gromov-Wasserstein distances for comparing such parametric data, including time-varying metric spaces induced by collective motion, temporally evolving weighted social networks, and random graph models. We establish foundational properties of these distances, showing that they subsume several existing metrics in the literature, and derive theoretical approximation guarantees. In particular, we develop computationally tractable lower bounds and relate them to graph statistics commonly used in random graph theory. Furthermore, we prove that our distances can be consistently approximated in random graph and random metric space settings via empirical estimates from generative models. Finally, we demonstrate the practical utility of our framework through a series of numerical experiments.

Conic Formulations of Transport Metrics for Unbalanced Measure Networks and Hypernetworks

The Gromov-Wasserstein (GW) variant of optimal transport, designed to compare probability densities defined over distinct metric spaces, has emerged as an important tool for the analysis of data with complex structure, such as ensembles of point clouds or networks. To overcome certain limitations, such as the restriction to comparisons of measures of equal mass and sensitivity to outliers, several unbalanced or partial transport relaxations of the GW distance have been introduced in the recent literature. This paper is concerned with the Conic Gromov-Wasserstein (CGW) distance introduced by S\'{e}journ\'{e}, Vialard, and Peyr\'{e}. We provide a novel formulation in terms of semi-couplings, and extend the framework beyond the metric measure space setting, to compare more general network and hypernetwork structures. With this new formulation, we establish several fundamental properties of the CGW metric, including its scaling behavior under dilation, variational convergence in the limit of volume growth constraints, and comparison bounds with established optimal transport metrics. We further derive quantitative bounds that characterize the robustness of the CGW metric to perturbations in the underlying measures. The hypernetwork formulation of CGW admits a simple and provably convergent block coordinate ascent algorithm for its estimation, and we demonstrate the computational tractability and scalability of our approach through experiments on synthetic and real-world high-dimensional and structured datasets.

Fused Gromov-Wasserstein Variance Decomposition with Linear Optimal Transport

Wasserstein distances form a family of metrics on spaces of probability measures that have recently seen many applications. However, statistical analysis in these spaces is complex due to the nonlinearity of Wasserstein spaces. One potential solution to this problem is Linear Optimal Transport (LOT). This method allows one to find a Euclidean embedding, called LOT embedding, of measures in some Wasserstein spaces, but some information is lost in this embedding. So, to understand whether statistical analysis relying on LOT embeddings can make valid inferences about original data, it is helpful to quantify how well these embeddings describe that data. To answer this question, we present a decomposition of the Fr\'echet variance of a set of measures in the 2-Wasserstein space, which allows one to compute the percentage of variance explained by LOT embeddings of those measures. We then extend this decomposition to the Fused Gromov-Wasserstein setting. We also present several experiments that explore the relationship between the dimension of the LOT embedding, the percentage of variance explained by the embedding, and the classification accuracy of machine learning classifiers built on the embedded data. We use the MNIST handwritten digits dataset, IMDB-50000 dataset, and Diffusion Tensor MRI images for these experiments. Our results illustrate the effectiveness of low dimensional LOT embeddings in terms of the percentage of variance explained and the classification accuracy of models built on the embedded data.

Metric properties of partial and robust Gromov-Wasserstein distances

The Gromov-Wasserstein (GW) distances define a family of metrics, based on ideas from optimal transport, which enable comparisons between probability measures defined on distinct metric spaces. They are particularly useful in areas such as network analysis and geometry processing, as computation of a GW distance involves solving for registration between the objects which minimizes geometric distortion. Although GW distances have proven useful for various applications in the recent machine learning literature, it has been observed that they are inherently sensitive to outlier noise and cannot accommodate partial matching. This has been addressed by various constructions building on the GW framework; in this article, we focus specifically on a natural relaxation of the GW optimization problem, introduced by Chapel et al., which is aimed at addressing exactly these shortcomings. Our goal is to understand the theoretical properties of this relaxed optimization problem, from the viewpoint of metric geometry. While the relaxed problem fails to induce a metric, we derive precise characterizations of how it fails the axioms of non-degeneracy and triangle inequality. These observations lead us to define a novel family of distances, whose construction is inspired by the Prokhorov and Ky Fan distances, as well as by the recent work of Raghvendra et al.\ on robust versions of classical Wasserstein distance. We show that our new distances define true metrics, that they induce the same topology as the GW distances, and that they enjoy additional robustness to perturbations. These results provide a mathematically rigorous basis for using our robust partial GW distances in applications where outliers and partial matching are concerns.

Geometry of the Space of Partitioned Networks: A Unified Theoretical and Computational Framework

Interactions and relations between objects may be pairwise or higher-order in nature, and so network-valued data are ubiquitous in the real world. The "space of networks", however, has a complex structure that cannot be adequately described using conventional statistical tools. We introduce a measure-theoretic formalism for modeling generalized network structures such as graphs, hypergraphs, or graphs whose nodes come with a partition into categorical classes. We then propose a metric that extends the Gromov-Wasserstein distance between graphs and the co-optimal transport distance between hypergraphs. We characterize the geometry of this space, thereby providing a unified theoretical treatment of generalized networks that encompasses the cases of pairwise, as well as higher-order, relations. In particular, we show that our metric is an Alexandrov space of non-negative curvature, and leverage this structure to define gradients for certain functionals commonly arising in geometric data analysis tasks. We extend our analysis to the setting where vertices have additional label information, and derive efficient computational schemes to use in practice. Equipped with these theoretical and computational tools, we demonstrate the utility of our framework in a suite of applications, including hypergraph alignment, clustering and dictionary learning from ensemble data, multi-omics alignment, as well as multiscale network alignment.

The Z-Gromov-Wasserstein Distance

The Gromov-Wasserstein (GW) distance is a powerful tool for comparing metric measure spaces which has found broad applications in data science and machine learning. Driven by the need to analyze datasets whose objects have increasingly complex structure (such as node and edge-attributed graphs), several variants of GW distance have been introduced in the recent literature. With a view toward establishing a general framework for the theory of GW-like distances, this paper considers a vast generalization of the notion of a metric measure space: for an arbitrary metric space $Z$, we define a $Z$-network to be a measure space endowed with a kernel valued in $Z$. We introduce a method for comparing $Z$-networks by defining a generalization of GW distance, which we refer to as $Z$-Gromov-Wasserstein ($Z$-GW) distance. This construction subsumes many previously known metrics and offers a unified approach to understanding their shared properties. The paper demonstrates that the $Z$-GW distance defines a metric on the space of $Z$-networks which retains desirable properties of $Z$, such as separability, completeness, and geodesicity. Many of these properties were unknown for existing variants of GW distance that fall under our framework. Our focus is on foundational theory, but our results also include computable lower bounds and approximations of the distance which will be useful for practical applications.

Quantized Gromov-Wasserstein

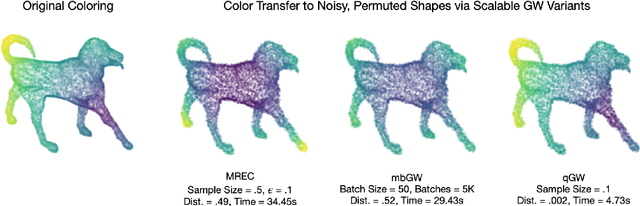
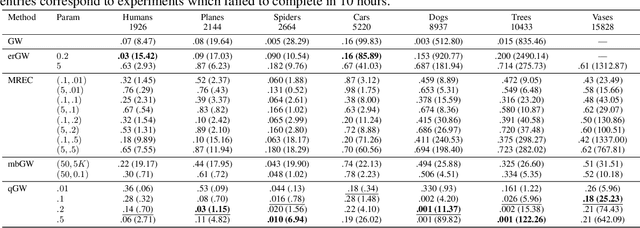
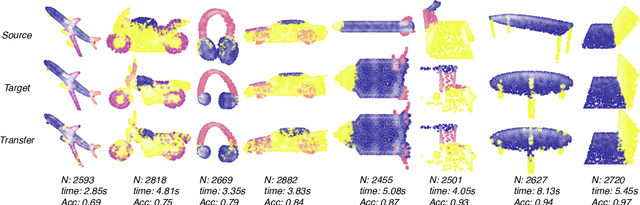
The Gromov-Wasserstein (GW) framework adapts ideas from optimal transport to allow for the comparison of probability distributions defined on different metric spaces. Scalable computation of GW distances and associated matchings on graphs and point clouds have recently been made possible by state-of-the-art algorithms such as S-GWL and MREC. Each of these algorithmic breakthroughs relies on decomposing the underlying spaces into parts and performing matchings on these parts, adding recursion as needed. While very successful in practice, theoretical guarantees on such methods are limited. Inspired by recent advances in the theory of quantization for metric measure spaces, we define Quantized Gromov Wasserstein (qGW): a metric that treats parts as fundamental objects and fits into a hierarchy of theoretical upper bounds for the GW problem. This formulation motivates a new algorithm for approximating optimal GW matchings which yields algorithmic speedups and reductions in memory complexity. Consequently, we are able to go beyond outperforming state-of-the-art and apply GW matching at scales that are an order of magnitude larger than in the existing literature, including datasets containing over 1M points.

Statistical shape analysis of brain arterial networks (BAN)

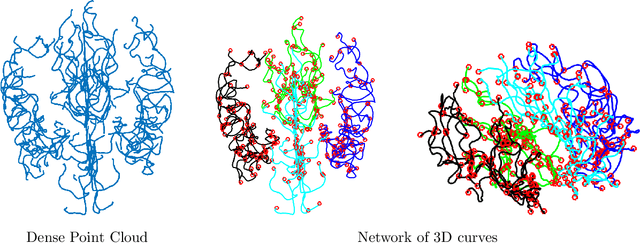
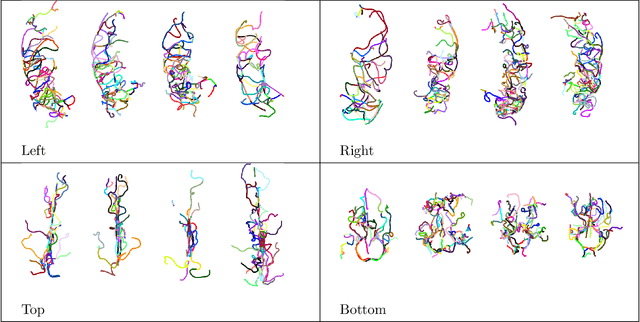
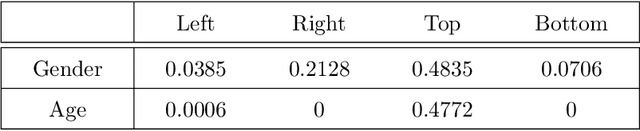
Structures of brain arterial networks (BANs) - that are complex arrangements of individual arteries, their branching patterns, and inter-connectivities - play an important role in characterizing and understanding brain physiology. One would like tools for statistically analyzing the shapes of BANs, i.e. quantify shape differences, compare population of subjects, and study the effects of covariates on these shapes. This paper mathematically represents and statistically analyzes BAN shapes as elastic shape graphs. Each elastic shape graph is made up of nodes that are connected by a number of 3D curves, and edges, with arbitrary shapes. We develop a mathematical representation, a Riemannian metric and other geometrical tools, such as computations of geodesics, means and covariances, and PCA for analyzing elastic graphs and BANs. This analysis is applied to BANs after separating them into four components -- top, bottom, left, and right. This framework is then used to generate shape summaries of BANs from 92 subjects, and to study the effects of age and gender on shapes of BAN components. We conclude that while gender effects require further investigation, the age has a clear, quantifiable effect on BAN shapes. Specifically, we find an increased variance in BAN shapes as age increases.

Generalized Spectral Clustering via Gromov-Wasserstein Learning

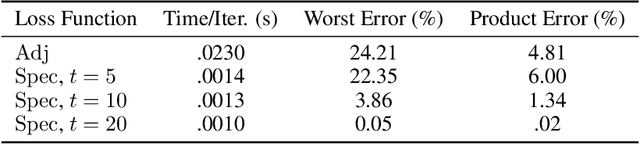
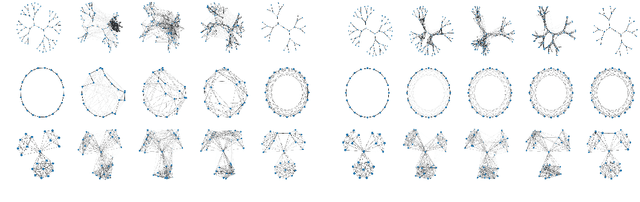
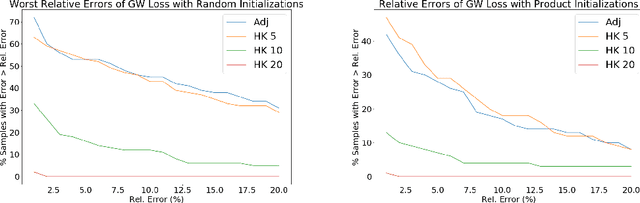
We establish a bridge between spectral clustering and Gromov-Wasserstein Learning (GWL), a recent optimal transport-based approach to graph partitioning. This connection both explains and improves upon the state-of-the-art performance of GWL. The Gromov-Wasserstein framework provides probabilistic correspondences between nodes of source and target graphs via a quadratic programming relaxation of the node matching problem. Our results utilize and connect the observations that the GW geometric structure remains valid for any rank-2 tensor, in particular the adjacency, distance, and various kernel matrices on graphs, and that the heat kernel outperforms the adjacency matrix in producing stable and informative node correspondences. Using the heat kernel in the GWL framework provides new multiscale graph comparisons without compromising theoretical guarantees, while immediately yielding improved empirical results. A key insight of the GWL framework toward graph partitioning was to compute GW correspondences from a source graph to a template graph with isolated, self-connected nodes. We show that when comparing against a two-node template graph using the heat kernel at the infinite time limit, the resulting partition agrees with the partition produced by the Fiedler vector. This in turn yields a new insight into the $k$-cut graph partitioning problem through the lens of optimal transport. Our experiments on a range of real-world networks achieve comparable results to, and in many cases outperform, the state-of-the-art achieved by GWL.

Gromov-Wasserstein Averaging in a Riemannian Framework

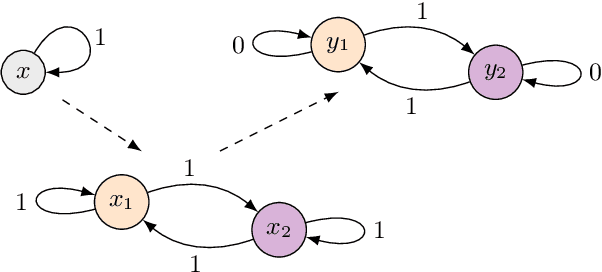
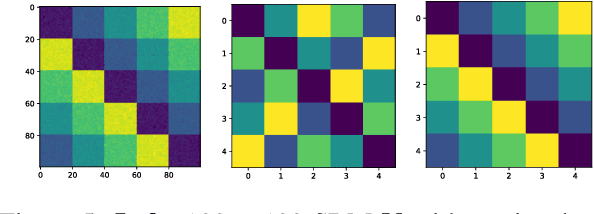
We introduce a theoretical framework for performing statistical tasks---including, but not limited to, averaging and principal component analysis---on the space of (possibly asymmetric) matrices with arbitrary entries and sizes. This is carried out under the lens of the Gromov-Wasserstein (GW) distance, and our methods translate the Riemannian framework of GW distances developed by Sturm into practical, implementable tools for network data analysis. Our methods are illustrated on datasets of asymmetric stochastic blockmodel networks and planar shapes viewed as metric spaces. On the theoretical front, we supplement the work of Sturm by producing additional results on the tangent structure of this "space of spaces", as well as on the gradient flow of the Fr\'{e}chet functional on this space.