Autonomous Robotic Ultrasound System for Liver Follow-up Diagnosis: Pilot Phantom Study

The paper introduces a novel autonomous robot ultrasound (US) system targeting liver follow-up scans for outpatients in local communities. Given a computed tomography (CT) image with specific target regions of interest, the proposed system carries out the autonomous follow-up scan in three steps: (i) initial robot contact to surface, (ii) coordinate mapping between CT image and robot, and (iii) target US scan. Utilizing 3D US-CT registration and deep learning-based segmentation networks, we can achieve precise imaging of 3D hepatic veins, facilitating accurate coordinate mapping between CT and the robot. This enables the automatic localization of follow-up targets within the CT image, allowing the robot to navigate precisely to the target's surface. Evaluation of the ultrasound phantom confirms the quality of the US-CT registration and shows the robot reliably locates the targets in repeated trials. The proposed framework holds the potential to significantly reduce time and costs for healthcare providers, clinicians, and follow-up patients, thereby addressing the increasing healthcare burden associated with chronic disease in local communities.

Non-asymptotic System Identification for Linear Systems with Nonlinear Policies

This paper considers a single-trajectory system identification problem for linear systems under general nonlinear and/or time-varying policies with i.i.d. random excitation noises. The problem is motivated by safe learning-based control for constrained linear systems, where the safe policies during the learning process are usually nonlinear and time-varying for satisfying the state and input constraints. In this paper, we provide a non-asymptotic error bound for least square estimation when the data trajectory is generated by any nonlinear and/or time-varying policies as long as the generated state and action trajectories are bounded. This significantly generalizes the existing non-asymptotic guarantees for linear system identification, which usually consider i.i.d. random inputs or linear policies. Interestingly, our error bound is consistent with that for linear policies with respect to the dependence on the trajectory length, system dimensions, and excitation levels. Lastly, we demonstrate the applications of our results by safe learning with robust model predictive control and provide numerical analysis.

Gaussian Max-Value Entropy Search for Multi-Agent Bayesian Optimization

We study the multi-agent Bayesian optimization (BO) problem, where multiple agents maximize a black-box function via iterative queries. We focus on Entropy Search (ES), a sample-efficient BO algorithm that selects queries to maximize the mutual information about the maximum of the black-box function. One of the main challenges of ES is that calculating the mutual information requires computationally-costly approximation techniques. For multi-agent BO problems, the computational cost of ES is exponential in the number of agents. To address this challenge, we propose the Gaussian Max-value Entropy Search, a multi-agent BO algorithm with favorable sample and computational efficiency. The key to our idea is to use a normal distribution to approximate the function maximum and calculate its mutual information accordingly. The resulting approximation allows queries to be cast as the solution of a closed-form optimization problem which, in turn, can be solved via a modified gradient ascent algorithm and scaled to a large number of agents. We demonstrate the effectiveness of Gaussian max-value Entropy Search through numerical experiments on standard test functions and real-robot experiments on the source-seeking problem. Results show that the proposed algorithm outperforms the multi-agent BO baselines in the numerical experiments and can stably seek the source with a limited number of noisy observations on real robots.

Distributed Information-based Source Seeking

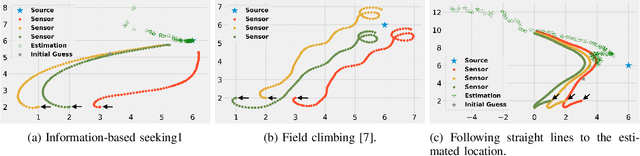
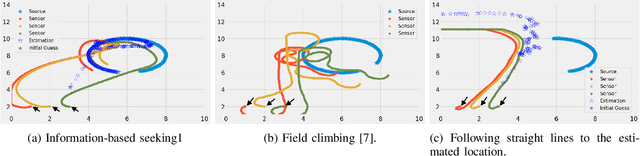
In this paper, we design an information-based multi-robot source seeking algorithm where a group of mobile sensors localizes and moves close to a single source using only local range-based measurements. In the algorithm, the mobile sensors perform source identification/localization to estimate the source location; meanwhile, they move to new locations to maximize the Fisher information about the source contained in the sensor measurements. In doing so, they improve the source location estimate and move closer to the source. Our algorithm is superior in convergence speed compared with traditional field climbing algorithms, is flexible in the measurement model and the choice of information metric, and is robust to measurement model errors. Moreover, we provide a fully distributed version of our algorithm, where each sensor decides its own actions and only shares information with its neighbors through a sparse communication network. We perform intensive simulation experiments to test our algorithms on large-scale systems and physical experiments on small ground vehicles with light sensors, demonstrating success in seeking a light source.

Multi-armed Bandit Learning on a Graph

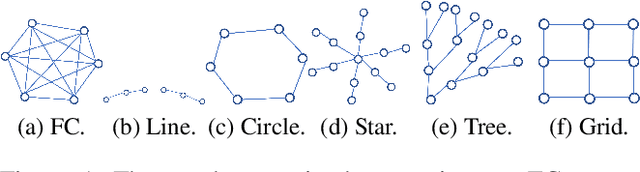
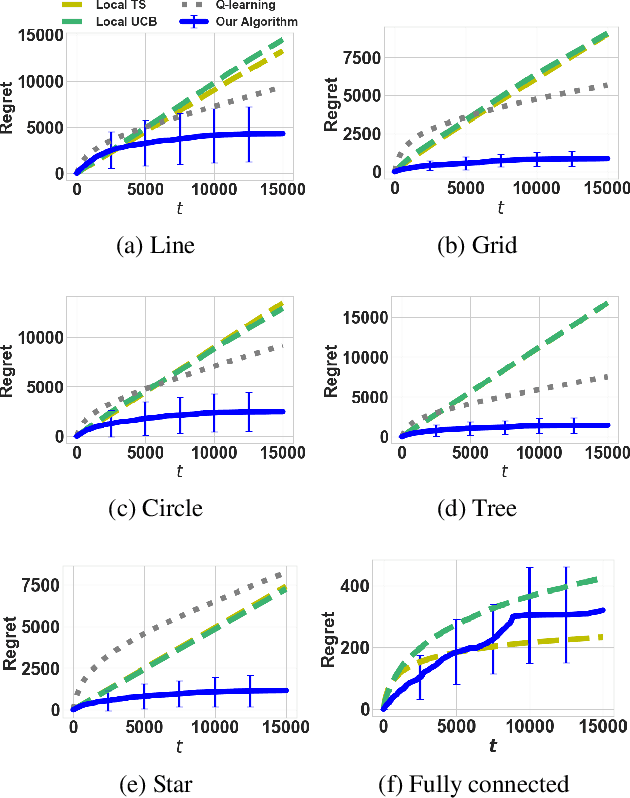
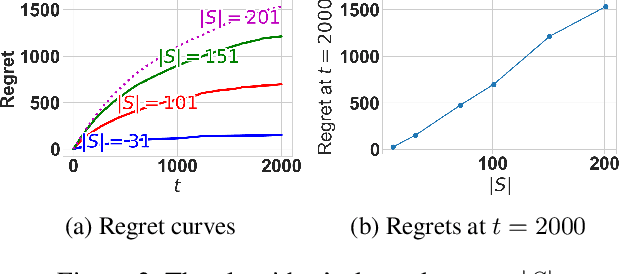
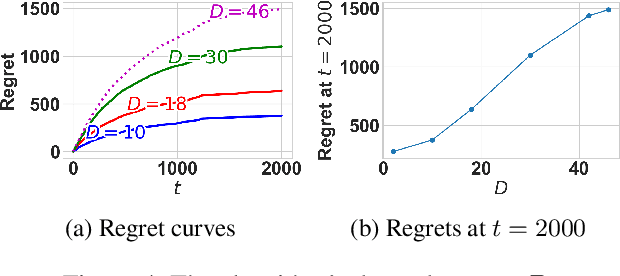
The multi-armed bandit(MAB) problem is a simple yet powerful framework that has been extensively studied in the context of decision-making under uncertainty. In many real-world applications, such as robotic applications, selecting an arm corresponds to a physical action that constrains the choices of the next available arms (actions). Motivated by this, we study an extension of MAB called the graph bandit, where an agent travels over a graph trying to maximize the reward collected from different nodes. The graph defines the freedom of the agent in selecting the next available nodes at each step. We assume the graph structure is fully available, but the reward distributions are unknown. Built upon an offline graph-based planning algorithm and the principle of optimism, we design an online learning algorithm that balances long-term exploration-exploitation using the principle of optimism. We show that our proposed algorithm achieves $O(|S|\sqrt{T}\log(T)+D|S|\log T)$ learning regret, where $|S|$ is the number of nodes and $D$ is the diameter of the graph, which is superior compared to the best-known reinforcement learning algorithms under similar settings. Numerical experiments confirm that our algorithm outperforms several benchmarks. Finally, we present a synthetic robotic application modeled by the graph bandit framework, where a robot moves on a network of rural/suburban locations to provide high-speed internet access using our proposed algorithm.