Finding Moving-Band Statistical Arbitrages via Convex-Concave Optimization

We propose a new method for finding statistical arbitrages that can contain more assets than just the traditional pair. We formulate the problem as seeking a portfolio with the highest volatility, subject to its price remaining in a band and a leverage limit. This optimization problem is not convex, but can be approximately solved using the convex-concave procedure, a specific sequential convex programming method. We show how the method generalizes to finding moving-band statistical arbitrages, where the price band midpoint varies over time.

Multi-armed Bandit Learning on a Graph

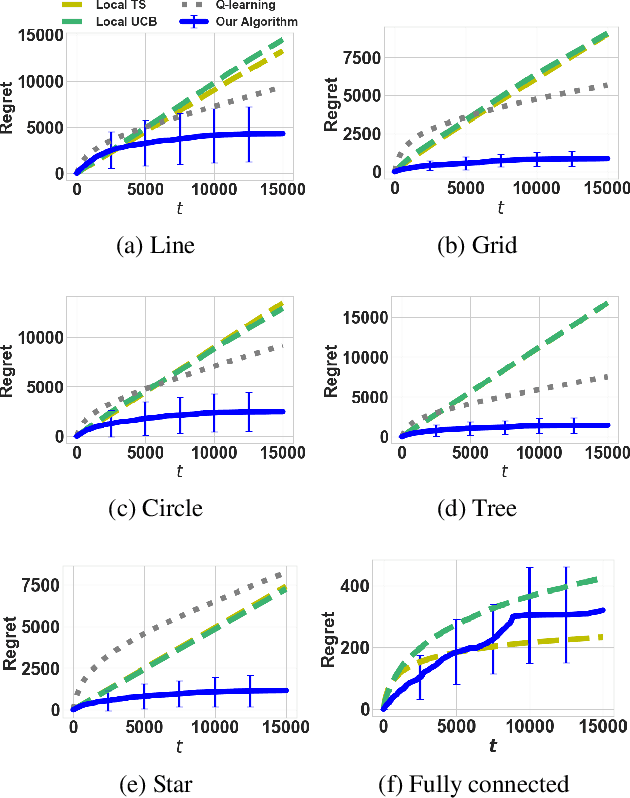
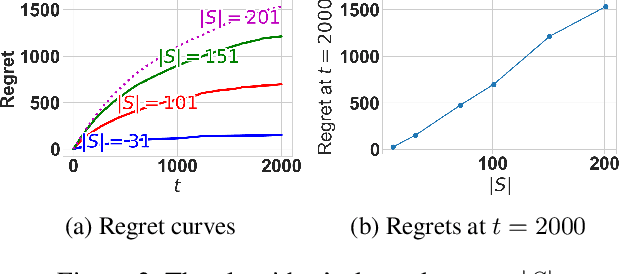
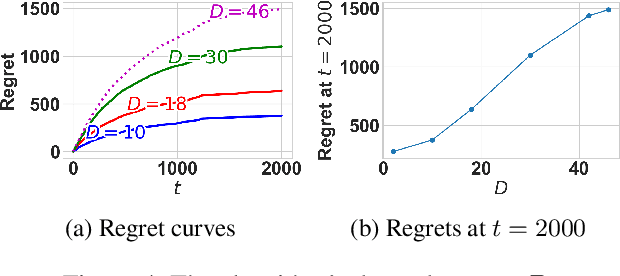
The multi-armed bandit(MAB) problem is a simple yet powerful framework that has been extensively studied in the context of decision-making under uncertainty. In many real-world applications, such as robotic applications, selecting an arm corresponds to a physical action that constrains the choices of the next available arms (actions). Motivated by this, we study an extension of MAB called the graph bandit, where an agent travels over a graph trying to maximize the reward collected from different nodes. The graph defines the freedom of the agent in selecting the next available nodes at each step. We assume the graph structure is fully available, but the reward distributions are unknown. Built upon an offline graph-based planning algorithm and the principle of optimism, we design an online learning algorithm that balances long-term exploration-exploitation using the principle of optimism. We show that our proposed algorithm achieves $O(|S|\sqrt{T}\log(T)+D|S|\log T)$ learning regret, where $|S|$ is the number of nodes and $D$ is the diameter of the graph, which is superior compared to the best-known reinforcement learning algorithms under similar settings. Numerical experiments confirm that our algorithm outperforms several benchmarks. Finally, we present a synthetic robotic application modeled by the graph bandit framework, where a robot moves on a network of rural/suburban locations to provide high-speed internet access using our proposed algorithm.

Mixed Observable RRT: Multi-Agent Mission-Planning in Partially Observable Environments

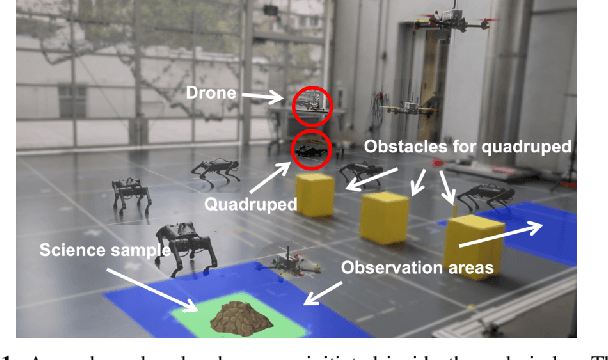
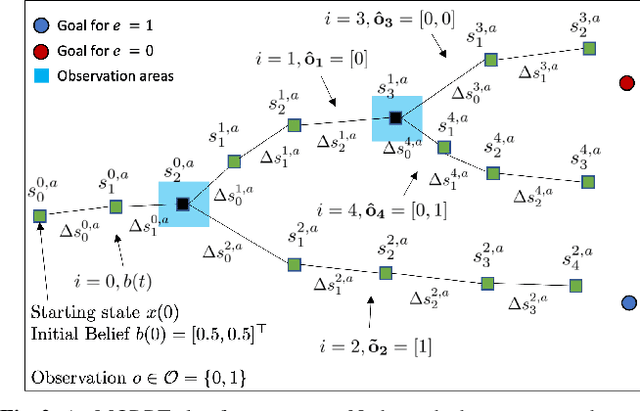
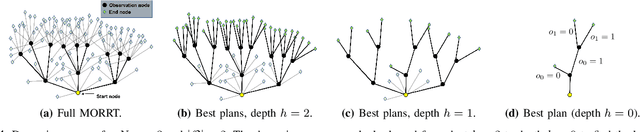
This paper considers centralized mission-planning for a heterogeneous multi-agent system with the aim of locating a hidden target. We propose a mixed observable setting, consisting of a fully observable state-space and a partially observable environment, using a hidden Markov model. First, we construct rapidly exploring random trees (RRTs) to introduce the mixed observable RRT for finding plausible mission plans giving way-points for each agent. Leveraging this construction, we present a path-selection strategy based on a dynamic programming approach, which accounts for the uncertainty from partial observations and minimizes the expected cost. Finally, we combine the high-level plan with model predictive controllers to evaluate the approach on an experimental setup consisting of a quadruped robot and a drone. It is shown that agents are able to make intelligent decisions to explore the area efficiently and to locate the target through collaborative actions.