Leveraging Public Data for Practical Private Query Release

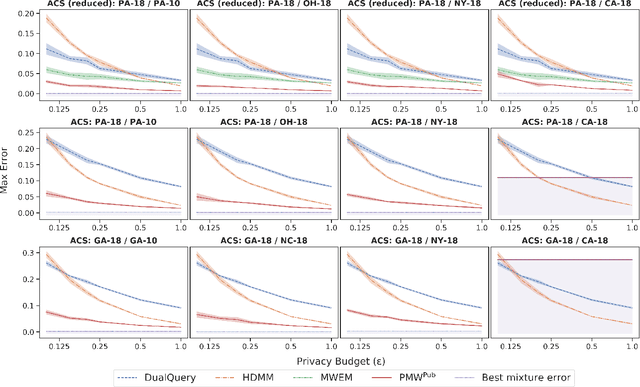
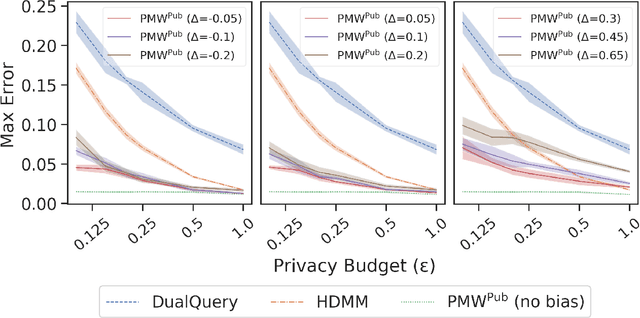
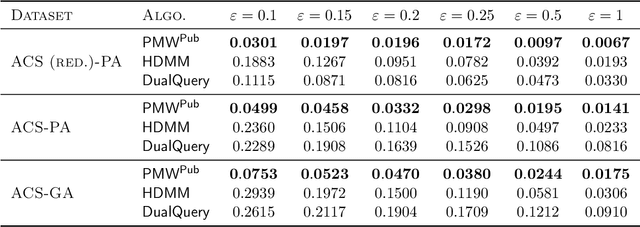
In many statistical problems, incorporating priors can significantly improve performance. However, the use of prior knowledge in differentially private query release has remained underexplored, despite such priors commonly being available in the form of public datasets, such as previous US Census releases. With the goal of releasing statistics about a private dataset, we present PMW^Pub, which -- unlike existing baselines -- leverages public data drawn from a related distribution as prior information. We provide a theoretical analysis and an empirical evaluation on the American Community Survey (ACS) and ADULT datasets, which shows that our method outperforms state-of-the-art methods. Furthermore, PMW^Pub scales well to high-dimensional data domains, where running many existing methods would be computationally infeasible.

The Distributed Discrete Gaussian Mechanism for Federated Learning with Secure Aggregation

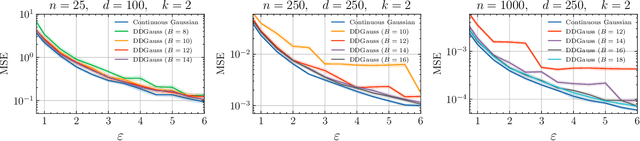
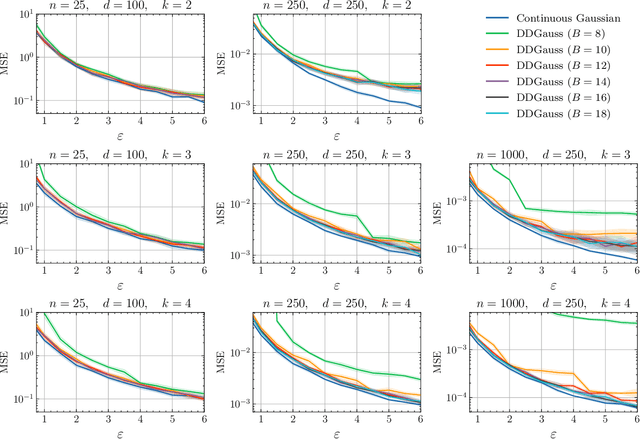
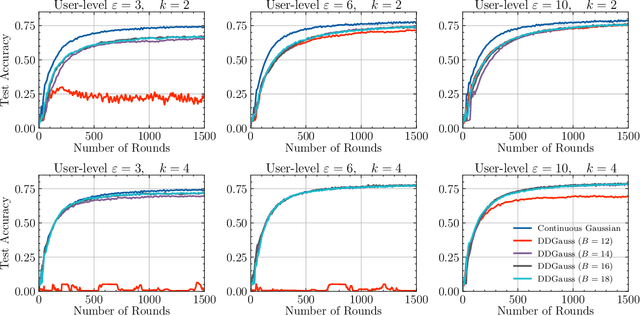
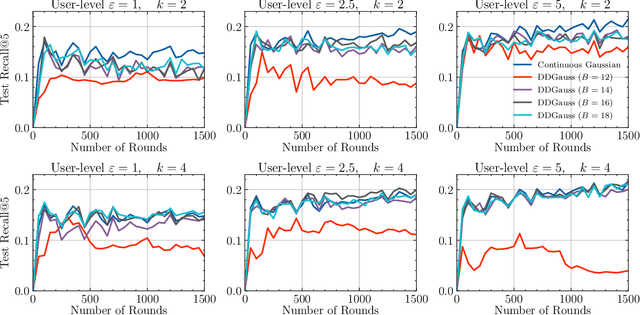
We consider training models on private data that is distributed across user devices. To ensure privacy, we add on-device noise and use secure aggregation so that only the noisy sum is revealed to the server. We present a comprehensive end-to-end system, which appropriately discretizes the data and adds discrete Gaussian noise before performing secure aggregation. We provide a novel privacy analysis for sums of discrete Gaussians. We also analyze the effect of rounding the input data and the modular summation arithmetic. Our theoretical guarantees highlight the complex tension between communication, privacy, and accuracy. Our extensive experimental results demonstrate that our solution is essentially able to achieve a comparable accuracy to central differential privacy with 16 bits of precision per value.

New Oracle-Efficient Algorithms for Private Synthetic Data Release

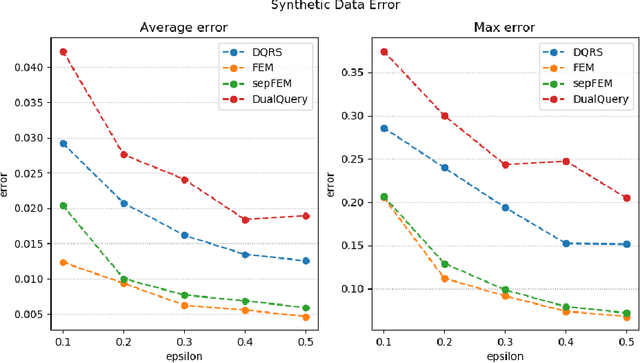
We present three new algorithms for constructing differentially private synthetic data---a sanitized version of a sensitive dataset that approximately preserves the answers to a large collection of statistical queries. All three algorithms are \emph{oracle-efficient} in the sense that they are computationally efficient when given access to an optimization oracle. Such an oracle can be implemented using many existing (non-private) optimization tools such as sophisticated integer program solvers. While the accuracy of the synthetic data is contingent on the oracle's optimization performance, the algorithms satisfy differential privacy even in the worst case. For all three algorithms, we provide theoretical guarantees for both accuracy and privacy. Through empirical evaluation, we demonstrate that our methods scale well with both the dimensionality of the data and the number of queries. Compared to the state-of-the-art method High-Dimensional Matrix Mechanism \cite{McKennaMHM18}, our algorithms provide better accuracy in the large workload and high privacy regime (corresponding to low privacy loss $\varepsilon$).

The Discrete Gaussian for Differential Privacy

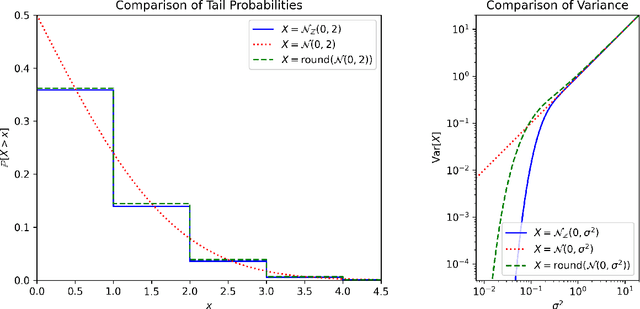
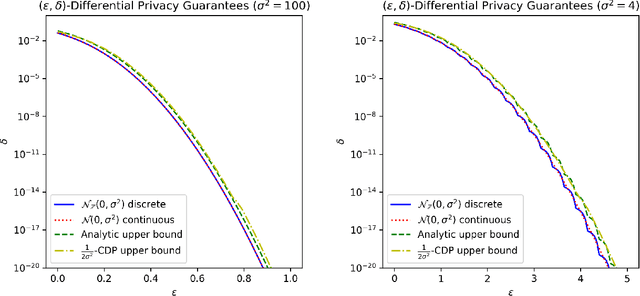
We show how to efficiently provide differentially private answers to counting queries (or integer-valued low-sensitivity queries) by adding discrete Gaussian noise, with essentially the same privacy and accuracy as the continuous Gaussian. The use of a discrete distribution is necessary in practice, as finite computers cannot represent samples from continuous distributions and numerical errors may destroy the privacy guarantee.

Reasoning About Generalization via Conditional Mutual Information

We provide an information-theoretic framework for studying the generalization properties of machine learning algorithms. Our framework ties together existing approaches, including uniform convergence bounds and recent methods for adaptive data analysis. Specifically, we use Conditional Mutual Information (CMI) to quantify how well the input (i.e., the training data) can be recognized given the output (i.e., the trained model) of the learning algorithm. We show that bounds on CMI can be obtained from VC dimension, compression schemes, differential privacy, and other methods. We then show that bounded CMI implies various forms of generalization.

Private Hypothesis Selection

We provide a differentially private algorithm for hypothesis selection. Given samples from an unknown probability distribution $P$ and a set of $m$ probability distributions $\mathcal{H}$, the goal is to output, in a $\varepsilon$-differentially private manner, a distribution from $\mathcal{H}$ whose total variation distance to $P$ is comparable to that of the best such distribution (which we denote by $\alpha$). The sample complexity of our basic algorithm is $O\left(\frac{\log m}{\alpha^2} + \frac{\log m}{\alpha \varepsilon}\right)$, representing a minimal cost for privacy when compared to the non-private algorithm. We also can handle infinite hypothesis classes $\mathcal{H}$ by relaxing to $(\varepsilon,\delta)$-differential privacy. We apply our hypothesis selection algorithm to give learning algorithms for a number of natural distribution classes, including Gaussians, product distributions, sums of independent random variables, piecewise polynomials, and mixture classes. Our hypothesis selection procedure allows us to generically convert a cover for a class to a learning algorithm, complementing known learning lower bounds which are in terms of the size of the packing number of the class. As the covering and packing numbers are often closely related, for constant $\alpha$, our algorithms achieve the optimal sample complexity for many classes of interest. Finally, we describe an application to private distribution-free PAC learning.

A Hybrid Approach to Privacy-Preserving Federated Learning

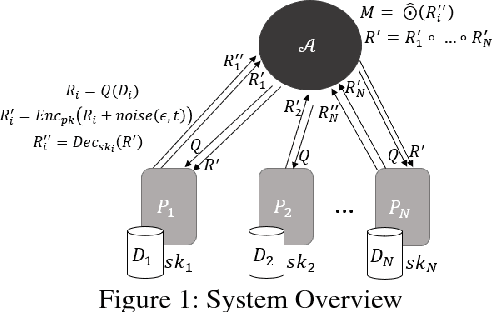
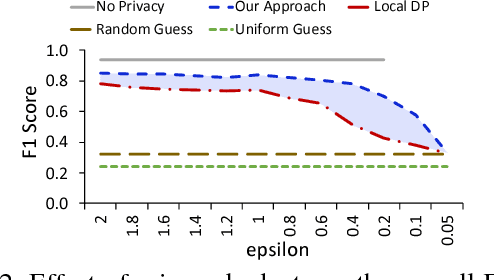
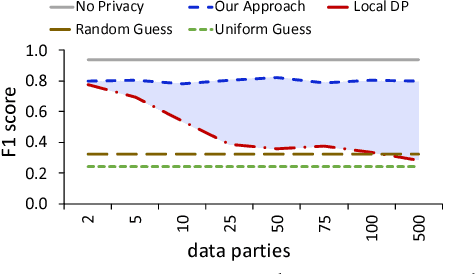
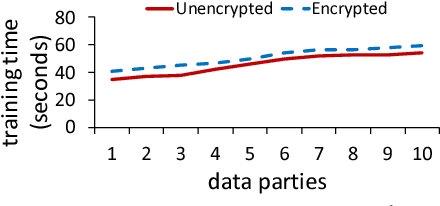
Training machine learning models often requires data from multiple parties. However, in some cases, data owners cannot share their data due to legal or privacy constraints but would still benefit from training a model jointly with multiple parties. Federated learning has arisen as an alternative to allow for the collaborative training of models without the sharing of raw data. However, attacks in the literature have demonstrated that simply maintaining data locally during training processes does not provide strong enough privacy guarantees. We need a federated learning system capable of preventing inference over the messages exchanged between parties during training as well as the final, trained model, considering potential collusion between parties, and ensuring the resulting machine learning model has acceptable predictive accuracy. Currently, existing approaches are either vulnerable to inference or do not scale for a large number of parties, resulting in models with low accuracy. To close this gap, we present a scalable approach that protects against these threats while producing models with high accuracy. Our approach provides formal data privacy guarantees using both differential privacy and secure multiparty computation frameworks. We validate our system with experimental results on two popular and significantly different machine learning algorithms: decision trees and convolutional neural networks. To the best of our knowledge, this presents the first approach to accurately train a neural network in a private, federated fashion. Our experiments demonstrate that our approach outperforms state of the art solutions in accuracy, customizability, and scalability.

The Limits of Post-Selection Generalization

While statistics and machine learning offers numerous methods for ensuring generalization, these methods often fail in the presence of adaptivity---the common practice in which the choice of analysis depends on previous interactions with the same dataset. A recent line of work has introduced powerful, general purpose algorithms that ensure post hoc generalization (also called robust or post-selection generalization), which says that, given the output of the algorithm, it is hard to find any statistic for which the data differs significantly from the population it came from. In this work we show several limitations on the power of algorithms satisfying post hoc generalization. First, we show a tight lower bound on the error of any algorithm that satisfies post hoc generalization and answers adaptively chosen statistical queries, showing a strong barrier to progress in post selection data analysis. Second, we show that post hoc generalization is not closed under composition, despite many examples of such algorithms exhibiting strong composition properties.

Calibrating Noise to Variance in Adaptive Data Analysis

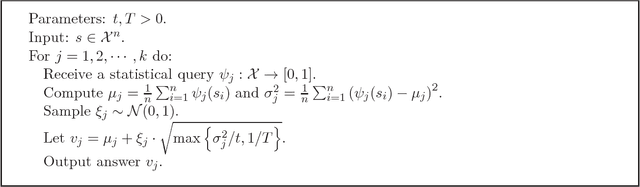
Datasets are often used multiple times and each successive analysis may depend on the outcome of previous analyses. Standard techniques for ensuring generalization and statistical validity do not account for this adaptive dependence. A recent line of work studies the challenges that arise from such adaptive data reuse by considering the problem of answering a sequence of "queries" about the data distribution where each query may depend arbitrarily on answers to previous queries. The strongest results obtained for this problem rely on differential privacy -- a strong notion of algorithmic stability with the important property that it "composes" well when data is reused. However the notion is rather strict, as it requires stability under replacement of an arbitrary data element. The simplest algorithm is to add Gaussian (or Laplace) noise to distort the empirical answers. However, analysing this technique using differential privacy yields suboptimal accuracy guarantees when the queries have low variance. Here we propose a relaxed notion of stability that also composes adaptively. We demonstrate that a simple and natural algorithm based on adding noise scaled to the standard deviation of the query provides our notion of stability. This implies an algorithm that can answer statistical queries about the dataset with substantially improved accuracy guarantees for low-variance queries. The only previous approach that provides such accuracy guarantees is based on a more involved differentially private median-of-means algorithm and its analysis exploits stronger "group" stability of the algorithm.

Generalization for Adaptively-chosen Estimators via Stable Median

Datasets are often reused to perform multiple statistical analyses in an adaptive way, in which each analysis may depend on the outcomes of previous analyses on the same dataset. Standard statistical guarantees do not account for these dependencies and little is known about how to provably avoid overfitting and false discovery in the adaptive setting. We consider a natural formalization of this problem in which the goal is to design an algorithm that, given a limited number of i.i.d.~samples from an unknown distribution, can answer adaptively-chosen queries about that distribution. We present an algorithm that estimates the expectations of $k$ arbitrary adaptively-chosen real-valued estimators using a number of samples that scales as $\sqrt{k}$. The answers given by our algorithm are essentially as accurate as if fresh samples were used to evaluate each estimator. In contrast, prior work yields error guarantees that scale with the worst-case sensitivity of each estimator. We also give a version of our algorithm that can be used to verify answers to such queries where the sample complexity depends logarithmically on the number of queries $k$ (as in the reusable holdout technique). Our algorithm is based on a simple approximate median algorithm that satisfies the strong stability guarantees of differential privacy. Our techniques provide a new approach for analyzing the generalization guarantees of differentially private algorithms.