Why Is Public Pretraining Necessary for Private Model Training?

In the privacy-utility tradeoff of a model trained on benchmark language and vision tasks, remarkable improvements have been widely reported with the use of pretraining on publicly available data. This is in part due to the benefits of transfer learning, which is the standard motivation for pretraining in non-private settings. However, the stark contrast in the improvement achieved through pretraining under privacy compared to non-private settings suggests that there may be a deeper, distinct cause driving these gains. To explain this phenomenon, we hypothesize that the non-convex loss landscape of a model training necessitates an optimization algorithm to go through two phases. In the first, the algorithm needs to select a good "basin" in the loss landscape. In the second, the algorithm solves an easy optimization within that basin. The former is a harder problem to solve with private data, while the latter is harder to solve with public data due to a distribution shift or data scarcity. Guided by this intuition, we provide theoretical constructions that provably demonstrate the separation between private training with and without public pretraining. Further, systematic experiments on CIFAR10 and LibriSpeech provide supporting evidence for our hypothesis.

Tight Auditing of Differentially Private Machine Learning

Auditing mechanisms for differential privacy use probabilistic means to empirically estimate the privacy level of an algorithm. For private machine learning, existing auditing mechanisms are tight: the empirical privacy estimate (nearly) matches the algorithm's provable privacy guarantee. But these auditing techniques suffer from two limitations. First, they only give tight estimates under implausible worst-case assumptions (e.g., a fully adversarial dataset). Second, they require thousands or millions of training runs to produce non-trivial statistical estimates of the privacy leakage. This work addresses both issues. We design an improved auditing scheme that yields tight privacy estimates for natural (not adversarially crafted) datasets -- if the adversary can see all model updates during training. Prior auditing works rely on the same assumption, which is permitted under the standard differential privacy threat model. This threat model is also applicable, e.g., in federated learning settings. Moreover, our auditing scheme requires only two training runs (instead of thousands) to produce tight privacy estimates, by adapting recent advances in tight composition theorems for differential privacy. We demonstrate the utility of our improved auditing schemes by surfacing implementation bugs in private machine learning code that eluded prior auditing techniques.

A Bias-Variance-Privacy Trilemma for Statistical Estimation

The canonical algorithm for differentially private mean estimation is to first clip the samples to a bounded range and then add noise to their empirical mean. Clipping controls the sensitivity and, hence, the variance of the noise that we add for privacy. But clipping also introduces statistical bias. We prove that this tradeoff is inherent: no algorithm can simultaneously have low bias, low variance, and low privacy loss for arbitrary distributions. On the positive side, we show that unbiased mean estimation is possible under approximate differential privacy if we assume that the distribution is symmetric. Furthermore, we show that, even if we assume that the data is sampled from a Gaussian, unbiased mean estimation is impossible under pure or concentrated differential privacy.

Composition of Differential Privacy & Privacy Amplification by Subsampling

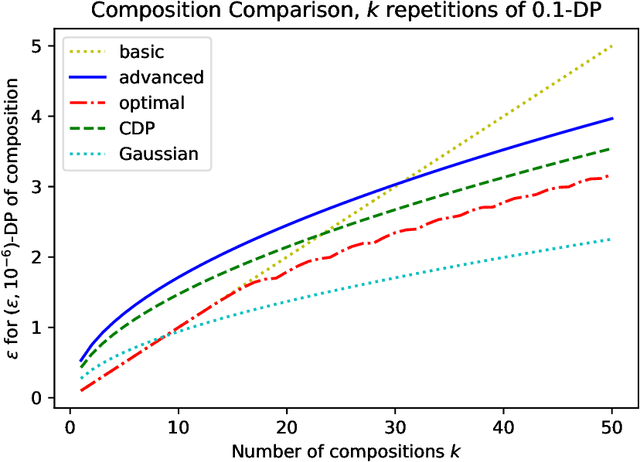
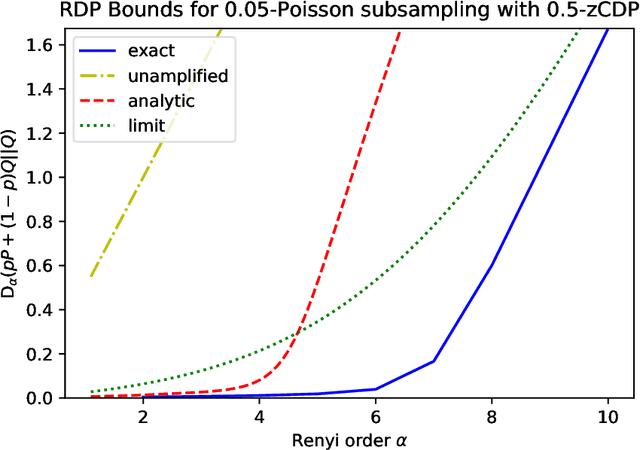
This chapter is meant to be part of the book "Differential Privacy for Artificial Intelligence Applications." We give an introduction to the most important property of differential privacy -- composition: running multiple independent analyses on the data of a set of people will still be differentially private as long as each of the analyses is private on its own -- as well as the related topic of privacy amplification by subsampling. This chapter introduces the basic concepts and gives proofs of the key results needed to apply these tools in practice.

Algorithms with More Granular Differential Privacy Guarantees

Differential privacy is often applied with a privacy parameter that is larger than the theory suggests is ideal; various informal justifications for tolerating large privacy parameters have been proposed. In this work, we consider partial differential privacy (DP), which allows quantifying the privacy guarantee on a per-attribute basis. In this framework, we study several basic data analysis and learning tasks, and design algorithms whose per-attribute privacy parameter is smaller that the best possible privacy parameter for the entire record of a person (i.e., all the attributes).

Debugging Differential Privacy: A Case Study for Privacy Auditing

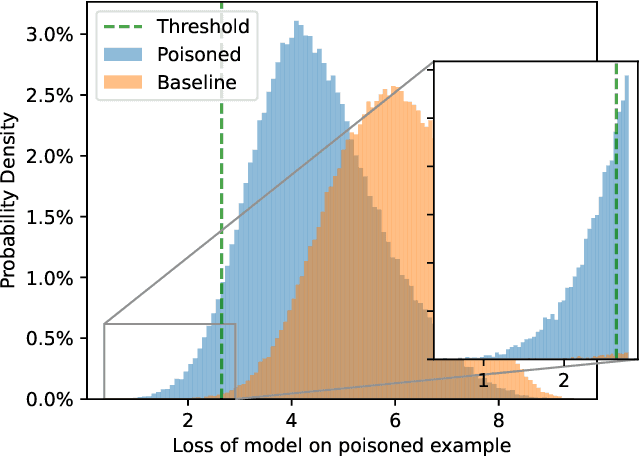
Differential Privacy can provide provable privacy guarantees for training data in machine learning. However, the presence of proofs does not preclude the presence of errors. Inspired by recent advances in auditing which have been used for estimating lower bounds on differentially private algorithms, here we show that auditing can also be used to find flaws in (purportedly) differentially private schemes. In this case study, we audit a recent open source implementation of a differentially private deep learning algorithm and find, with 99.99999999% confidence, that the implementation does not satisfy the claimed differential privacy guarantee.

Public Data-Assisted Mirror Descent for Private Model Training

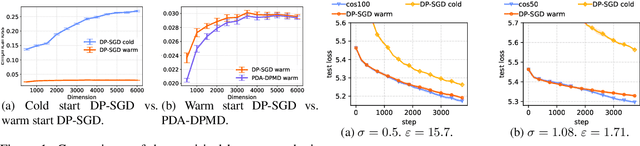
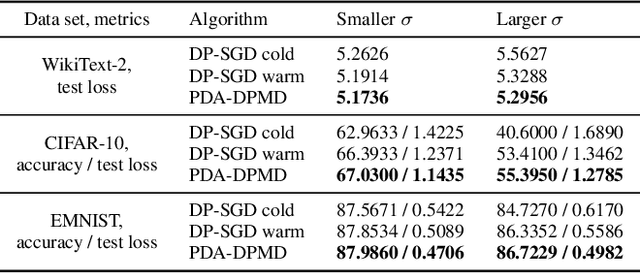
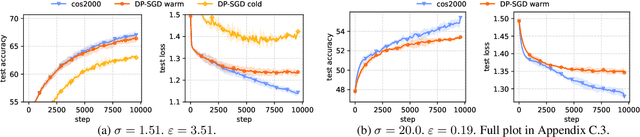
We revisit the problem of using public data to improve the privacy/utility trade-offs for differentially private (DP) model training. Here, public data refers to auxiliary data sets that have no privacy concerns. We consider public data that is from the same distribution as the private training data. For convex losses, we show that a variant of Mirror Descent provides population risk guarantees which are independent of the dimension of the model ($p$). Specifically, we apply Mirror Descent with the loss generated by the public data as the mirror map, and using DP gradients of the loss generated by the private (sensitive) data. To obtain dimension independence, we require $G_Q^2 \leq p$ public data samples, where $G_Q$ is a measure of the isotropy of the loss function. We further show that our algorithm has a natural ``noise stability'' property: If around the current iterate the public loss satisfies $\alpha_v$-strong convexity in a direction $v$, then using noisy gradients instead of the exact gradients shifts our next iterate in the direction $v$ by an amount proportional to $1/\alpha_v$ (in contrast with DP-SGD, where the shift is isotropic). Analogous results in prior works had to explicitly learn the geometry using the public data in the form of preconditioner matrices. Our method is also applicable to non-convex losses, as it does not rely on convexity assumptions to ensure DP guarantees. We demonstrate the empirical efficacy of our algorithm by showing privacy/utility trade-offs on linear regression, deep learning benchmark datasets (WikiText-2, CIFAR-10, and EMNIST), and in federated learning (StackOverflow). We show that our algorithm not only significantly improves over traditional DP-SGD and DP-FedAvg, which do not have access to public data, but also improves over DP-SGD and DP-FedAvg on models that have been pre-trained with the public data to begin with.

A Private and Computationally-Efficient Estimator for Unbounded Gaussians

We give the first polynomial-time, polynomial-sample, differentially private estimator for the mean and covariance of an arbitrary Gaussian distribution $\mathcal{N}(\mu,\Sigma)$ in $\mathbb{R}^d$. All previous estimators are either nonconstructive, with unbounded running time, or require the user to specify a priori bounds on the parameters $\mu$ and $\Sigma$. The primary new technical tool in our algorithm is a new differentially private preconditioner that takes samples from an arbitrary Gaussian $\mathcal{N}(0,\Sigma)$ and returns a matrix $A$ such that $A \Sigma A^T$ has constant condition number.

Hyperparameter Tuning with Renyi Differential Privacy

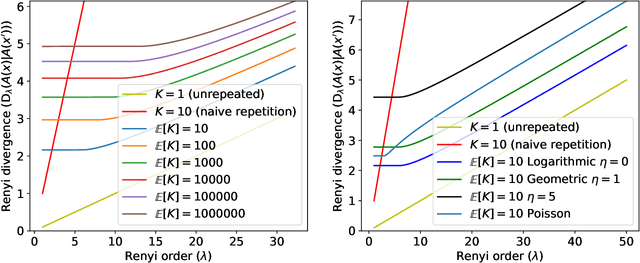
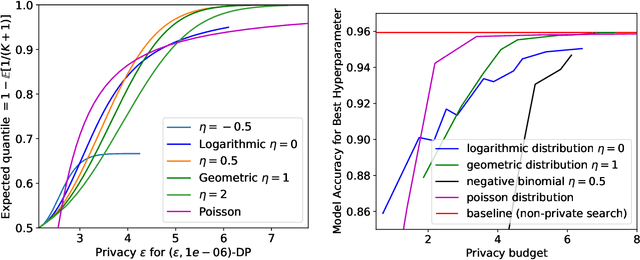
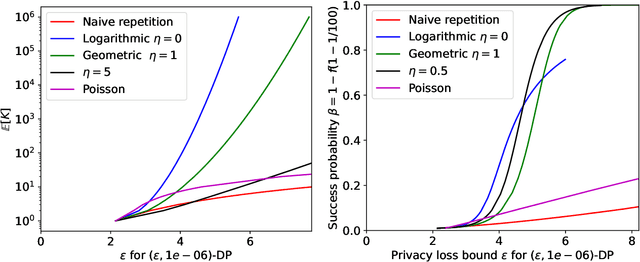
For many differentially private algorithms, such as the prominent noisy stochastic gradient descent (DP-SGD), the analysis needed to bound the privacy leakage of a single training run is well understood. However, few studies have reasoned about the privacy leakage resulting from the multiple training runs needed to fine tune the value of the training algorithm's hyperparameters. In this work, we first illustrate how simply setting hyperparameters based on non-private training runs can leak private information. Motivated by this observation, we then provide privacy guarantees for hyperparameter search procedures within the framework of Renyi Differential Privacy. Our results improve and extend the work of Liu and Talwar (STOC 2019). Our analysis supports our previous observation that tuning hyperparameters does indeed leak private information, but we prove that, under certain assumptions, this leakage is modest, as long as each candidate training run needed to select hyperparameters is itself differentially private.

PAC-Bayes, MAC-Bayes and Conditional Mutual Information: Fast rate bounds that handle general VC classes

We give a novel, unified derivation of conditional PAC-Bayesian and mutual information (MI) generalization bounds. We derive conditional MI bounds as an instance, with special choice of prior, of conditional MAC-Bayesian (Mean Approximately Correct) bounds, itself derived from conditional PAC-Bayesian bounds, where `conditional' means that one can use priors conditioned on a joint training and ghost sample. This allows us to get nontrivial PAC-Bayes and MI-style bounds for general VC classes, something recently shown to be impossible with standard PAC-Bayesian/MI bounds. Second, it allows us to get faster rates of order $O \left(({\text{KL}}/n)^{\gamma}\right)$ for $\gamma > 1/2$ if a Bernstein condition holds and for exp-concave losses (with $\gamma=1$), which is impossible with both standard PAC-Bayes generalization and MI bounds. Our work extends the recent work by Steinke and Zakynthinou [2020] who handle MI with VC but neither PAC-Bayes nor fast rates, the recent work of Hellstr\"om and Durisi [2020] who extend the latter to the PAC-Bayes setting via a unifying exponential inequality, and Mhammedi et al. [2019] who initiated fast rate PAC-Bayes generalization error bounds but handle neither MI nor general VC classes.