Total Deep Variation: A Stable Regularizer for Inverse Problems

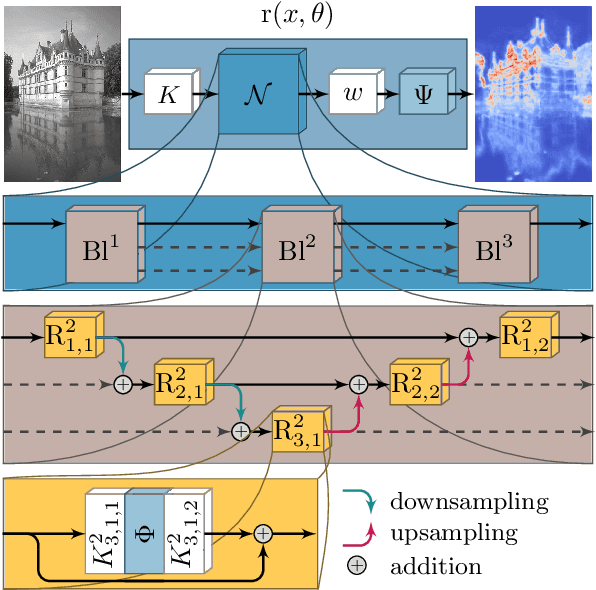
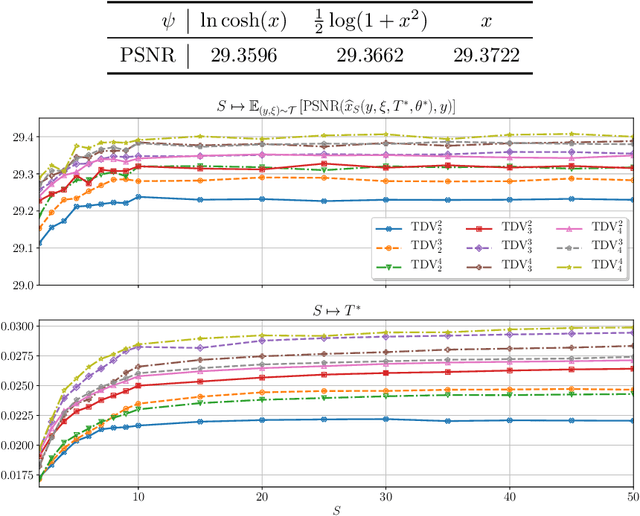
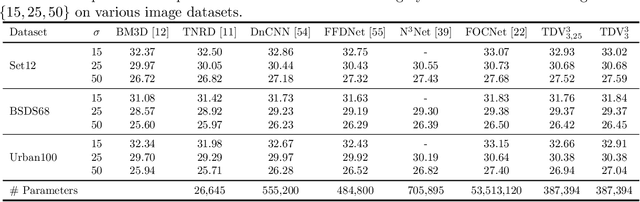
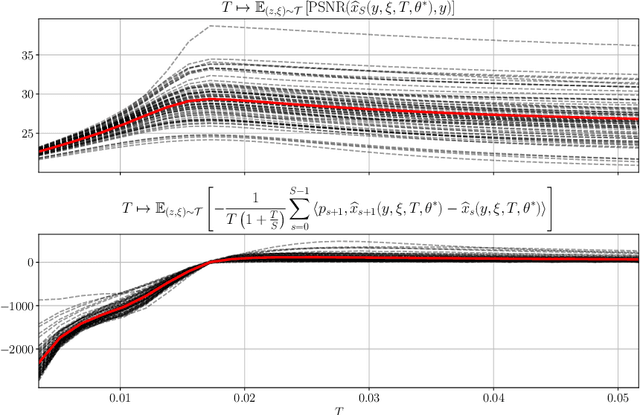
Various problems in computer vision and medical imaging can be cast as inverse problems. A frequent method for solving inverse problems is the variational approach, which amounts to minimizing an energy composed of a data fidelity term and a regularizer. Classically, handcrafted regularizers are used, which are commonly outperformed by state-of-the-art deep learning approaches. In this work, we combine the variational formulation of inverse problems with deep learning by introducing the data-driven general-purpose total deep variation regularizer. In its core, a convolutional neural network extracts local features on multiple scales and in successive blocks. This combination allows for a rigorous mathematical analysis including an optimal control formulation of the training problem in a mean-field setting and a stability analysis with respect to the initial values and the parameters of the regularizer. In addition, we experimentally verify the robustness against adversarial attacks and numerically derive upper bounds for the generalization error. Finally, we achieve state-of-the-art results for numerous imaging tasks.

Belief Propagation Reloaded: Learning BP-Layers for Labeling Problems

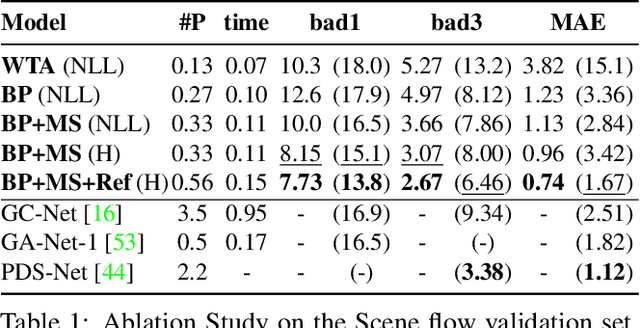
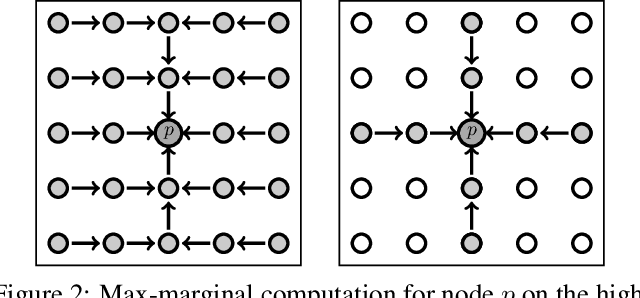
It has been proposed by many researchers that combining deep neural networks with graphical models can create more efficient and better regularized composite models. The main difficulties in implementing this in practice are associated with a discrepancy in suitable learning objectives as well as with the necessity of approximations for the inference. In this work we take one of the simplest inference methods, a truncated max-product Belief Propagation, and add what is necessary to make it a proper component of a deep learning model: We connect it to learning formulations with losses on marginals and compute the backprop operation. This BP-Layer can be used as the final or an intermediate block in convolutional neural networks (CNNs), allowing us to design a hierarchical model composing BP inference and CNNs at different scale levels. The model is applicable to a range of dense prediction problems, is well-trainable and provides parameter-efficient and robust solutions in stereo, optical flow and semantic segmentation.

Total Deep Variation for Linear Inverse Problems

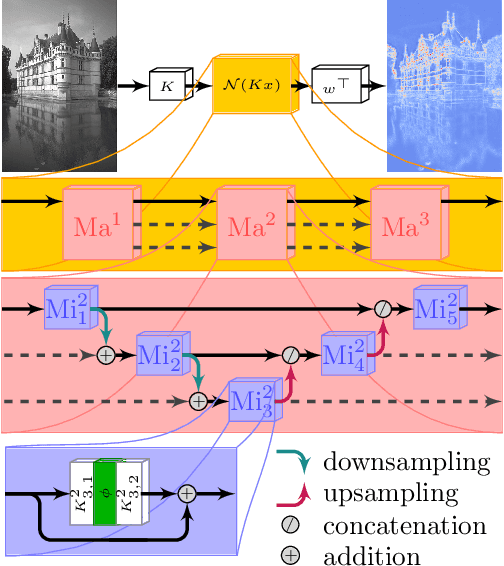
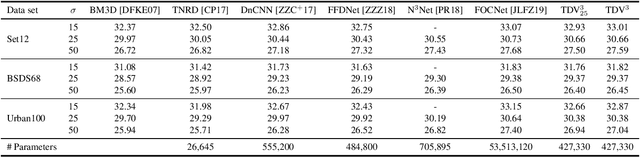
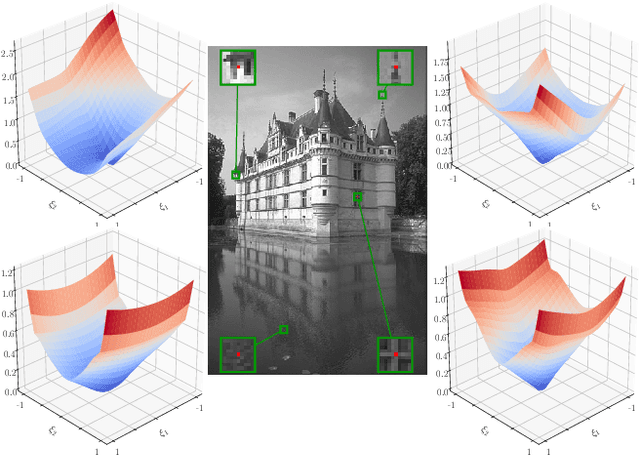
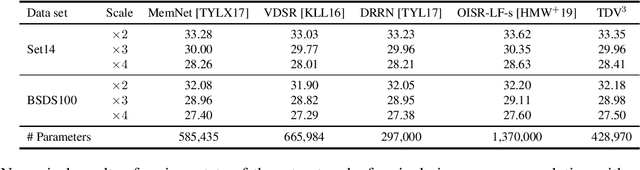
Diverse inverse problems in imaging can be cast as variational problems composed of a task-specific data fidelity term and a regularization term. In this paper, we propose a novel learnable general-purpose regularizer exploiting recent architectural design patterns from deep learning. We cast the learning problem as a discrete sampled optimal control problem, for which we derive the adjoint state equations and an optimality condition. By exploiting the variational structure of our approach, we perform a sensitivity analysis with respect to the learned parameters obtained from different training datasets. Moreover, we carry out a nonlinear eigenfunction analysis, which reveals interesting properties of the learned regularizer. We show state-of-the-art performance for classical image restoration and medical image reconstruction problems.

The Five Elements of Flow

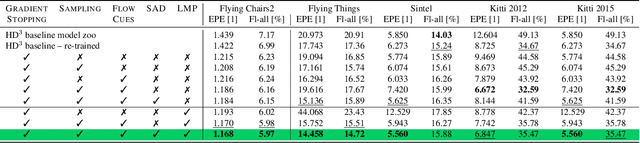
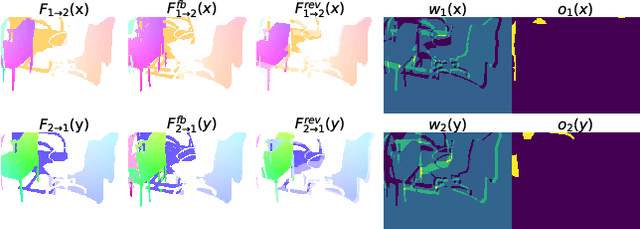
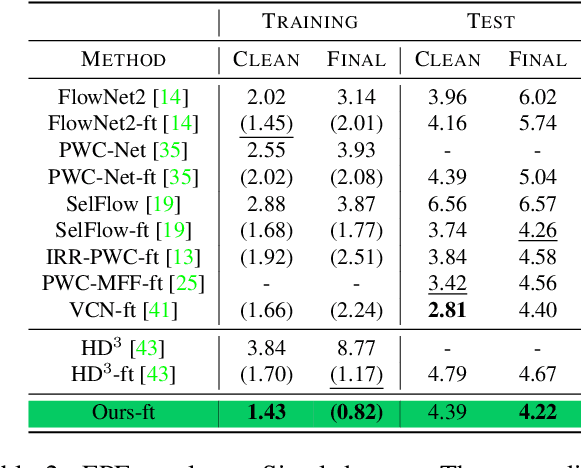
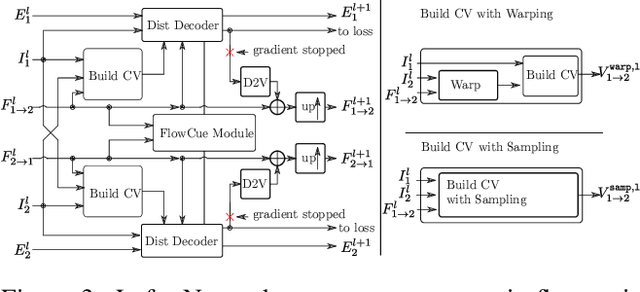
In this work we propose five concrete steps to improve the performance of optical flow algorithms. We carefully reviewed recently introduced innovations and well-established techniques in deep learning-based flow methods including i) pyramidal feature representations, ii) flow-based consistency checks, iii) cost volume construction practices or iv) distillation, and present extensions or alternatives to inhibiting factors we identified therein. We also show how changing the way gradients propagate in modern flow networks can lead to surprising boosts in performance. Finally, we contribute a novel feature that adaptively guides the learning process towards improving on under-performing flow predictions. Our findings are conceptually simple and easy to implement, yet result in compelling improvements on relevant error measures that we demonstrate via exhaustive ablations on datasets like Flying Chairs2, Flying Things, Sintel and KITTI. We establish new state-of-the-art results on the challenging Sintel and Kitti 2015 test datasets, and even show the portability of our findings to different optical flow and depth from stereo approaches.

On the estimation of the Wasserstein distance in generative models

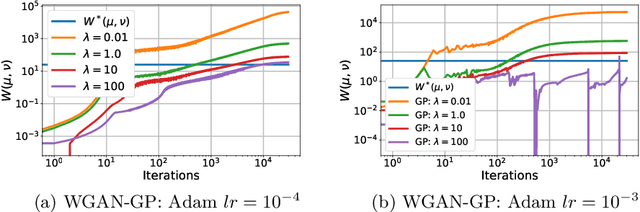
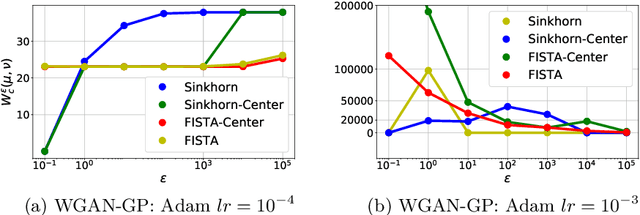
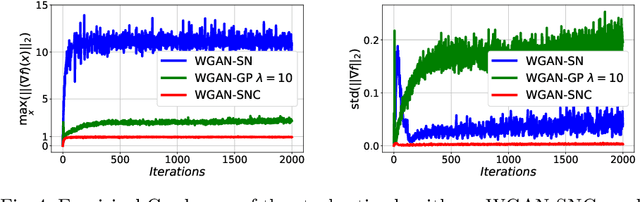
Generative Adversarial Networks (GANs) have been used to model the underlying probability distribution of sample based datasets. GANs are notoriuos for training difficulties and their dependence on arbitrary hyperparameters. One recent improvement in GAN literature is to use the Wasserstein distance as loss function leading to Wasserstein Generative Adversarial Networks (WGANs). Using this as a basis, we show various ways in which the Wasserstein distance is estimated for the task of generative modelling. Additionally, the secrets in training such models are shown and summarized at the end of this work. Where applicable, we extend current works to different algorithms, different cost functions, and different regularization schemes to improve generative models.

Learned Collaborative Stereo Refinement

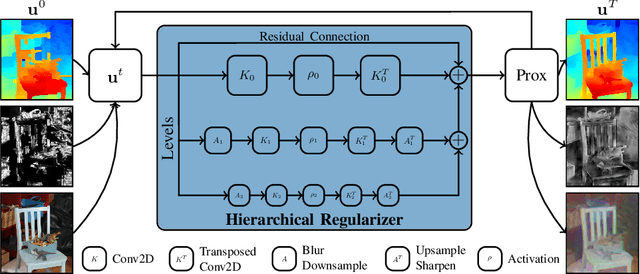
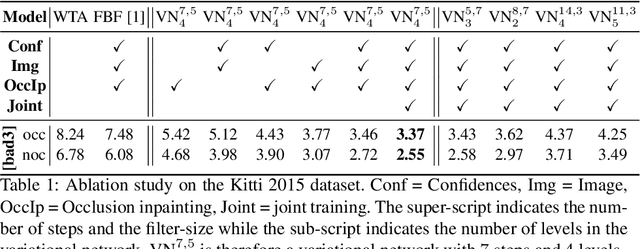
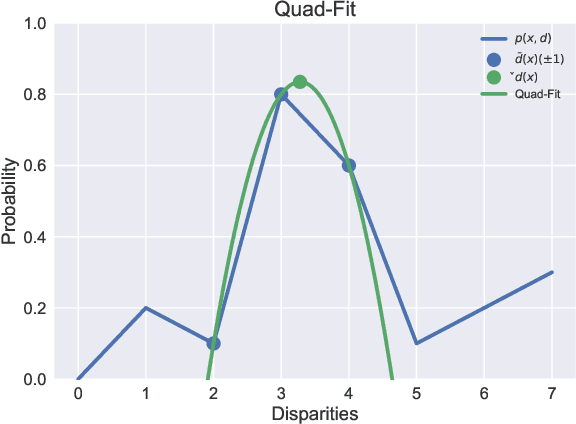
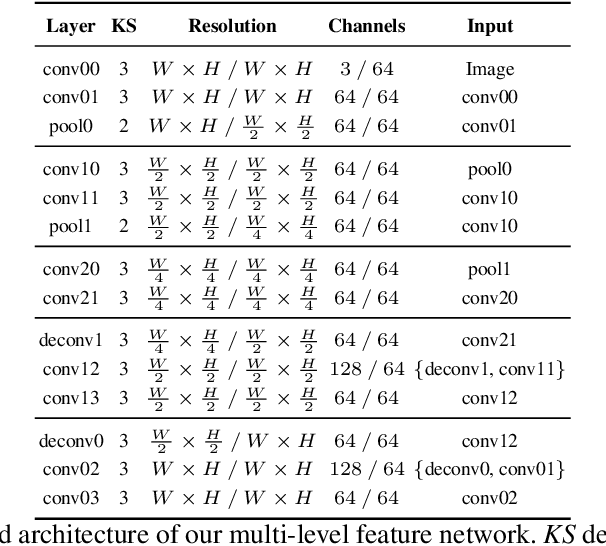
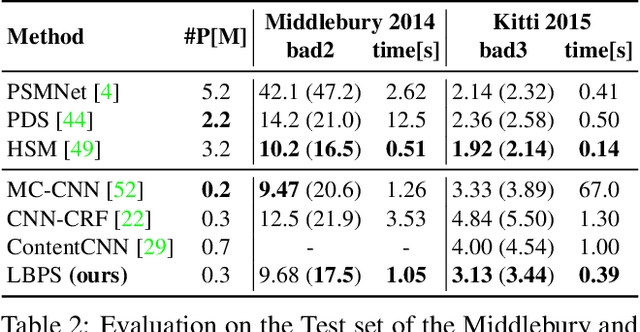
In this work, we propose a learning-based method to denoise and refine disparity maps of a given stereo method. The proposed variational network arises naturally from unrolling the iterates of a proximal gradient method applied to a variational energy defined in a joint disparity, color, and confidence image space. Our method allows to learn a robust collaborative regularizer leveraging the joint statistics of the color image, the confidence map and the disparity map. Due to the variational structure of our method, the individual steps can be easily visualized, thus enabling interpretability of the method. We can therefore provide interesting insights into how our method refines and denoises disparity maps. The efficiency of our method is demonstrated by the publicly available stereo benchmarks Middlebury 2014 and Kitti 2015.

Self-Supervised Learning for Stereo Reconstruction on Aerial Images

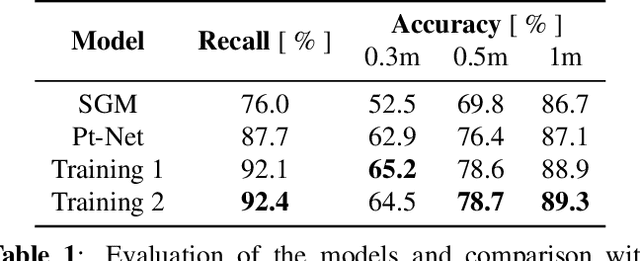
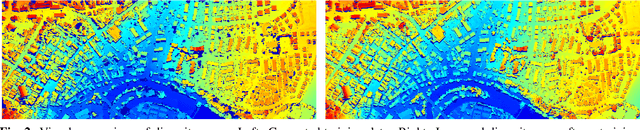
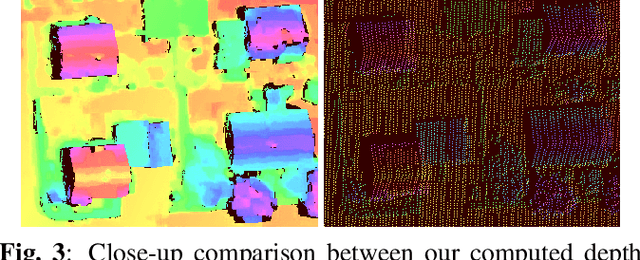
Recent developments established deep learning as an inevitable tool to boost the performance of dense matching and stereo estimation. On the downside, learning these networks requires a substantial amount of training data to be successful. Consequently, the application of these models outside of the laboratory is far from straight forward. In this work we propose a self-supervised training procedure that allows us to adapt our network to the specific (imaging) characteristics of the dataset at hand, without the requirement of external ground truth data. We instead generate interim training data by running our intermediate network on the whole dataset, followed by conservative outlier filtering. Bootstrapped from a pre-trained version of our hybrid CNN-CRF model, we alternate the generation of training data and network training. With this simple concept we are able to lift the completeness and accuracy of the pre-trained version significantly. We also show that our final model compares favorably to other popular stereo estimation algorithms on an aerial dataset.

An Optimal Control Approach to Early Stopping Variational Methods for Image Restoration

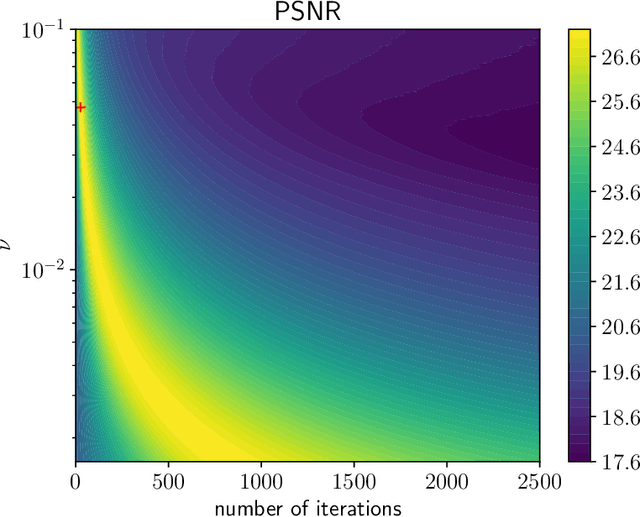
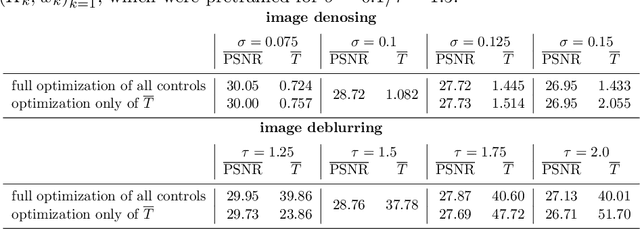
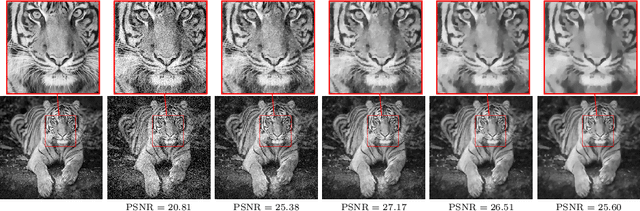
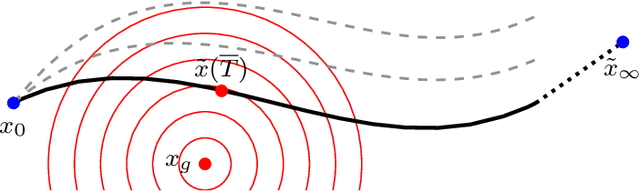
We investigate a well-known phenomenon of variational approaches in image processing, where typically the best image quality is achieved when the gradient flow process is stopped before converging to a stationary point. This paradox originates from a tradeoff between optimization and modelling errors of the underlying variational model and holds true even if deep learning methods are used to learn highly expressive regularizers from data. In this paper, we take advantage of this paradox and introduce an optimal stopping time into the gradient flow process, which in turn is learned from data by means of an optimal control approach. As a result, we obtain highly efficient numerical schemes that achieve competitive results for image denoising and image deblurring. A nonlinear spectral analysis of the gradient of the learned regularizer gives enlightening insights about the different regularization properties.

Fast Decomposable Submodular Function Minimization using Constrained Total Variation

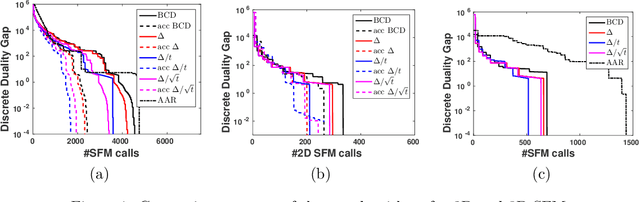
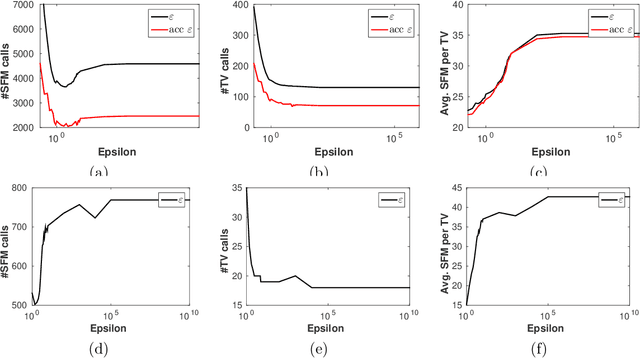
We consider the problem of minimizing the sum of submodular set functions assuming minimization oracles of each summand function. Most existing approaches reformulate the problem as the convex minimization of the sum of the corresponding Lov\'asz extensions and the squared Euclidean norm, leading to algorithms requiring total variation oracles of the summand functions; without further assumptions, these more complex oracles require many calls to the simpler minimization oracles often available in practice. In this paper, we consider a modified convex problem requiring constrained version of the total variation oracles that can be solved with significantly fewer calls to the simple minimization oracles. We support our claims by showing results on graph cuts for 2D and 3D graphs

Convex-Concave Backtracking for Inertial Bregman Proximal Gradient Algorithms in Non-Convex Optimization

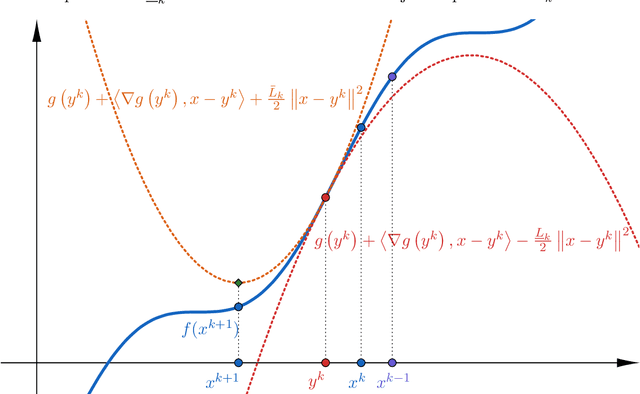
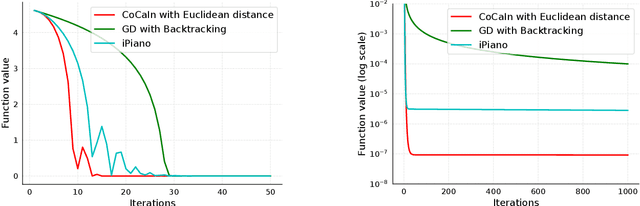
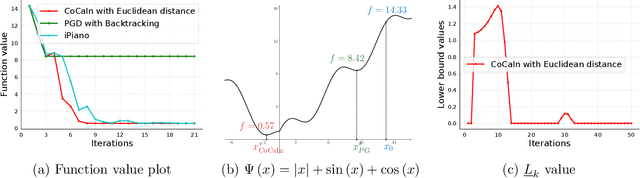
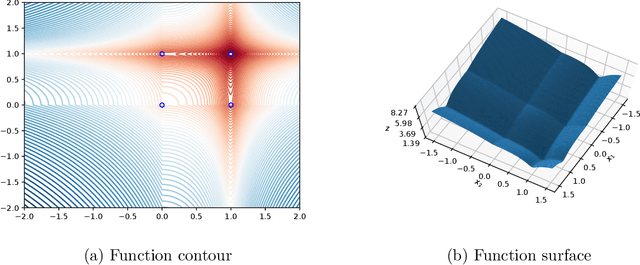
Backtracking line-search is an old yet powerful strategy for finding better step size to be used in proximal gradient algorithms. The main principle is to locally find a simple convex upper bound of the objective function, which in turn controls the step size that is used. In case of inertial proximal gradient algorithms, the situation becomes much more difficult and usually leads to very restrictive rules on the extrapolation parameter. In this paper, we show that the extrapolation parameter can be controlled by locally finding also a simple concave lower bound of the objective function. This gives rise to a double convex-concave backtracking procedure which allows for an adaptive and optimal choice of both the step size and extrapolation parameters. We apply this procedure to the class of inertial Bregman proximal gradient methods, and prove that any sequence generated converges globally to critical points of the function at hand. Numerical experiments on a number of challenging non-convex problems in image processing and machine learning were conducted and show the power of combining inertial step and double backtracking strategy in achieving improved performances.