Thanh V. Nguyen
Implicit Regularization for Group Sparsity
Jan 29, 2023



Abstract:We study the implicit regularization of gradient descent towards structured sparsity via a novel neural reparameterization, which we call a diagonally grouped linear neural network. We show the following intriguing property of our reparameterization: gradient descent over the squared regression loss, without any explicit regularization, biases towards solutions with a group sparsity structure. In contrast to many existing works in understanding implicit regularization, we prove that our training trajectory cannot be simulated by mirror descent. We analyze the gradient dynamics of the corresponding regression problem in the general noise setting and obtain minimax-optimal error rates. Compared to existing bounds for implicit sparse regularization using diagonal linear networks, our analysis with the new reparameterization shows improved sample complexity. In the degenerate case of size-one groups, our approach gives rise to a new algorithm for sparse linear regression. Finally, we demonstrate the efficacy of our approach with several numerical experiments.
Implicit Sparse Regularization: The Impact of Depth and Early Stopping
Aug 12, 2021
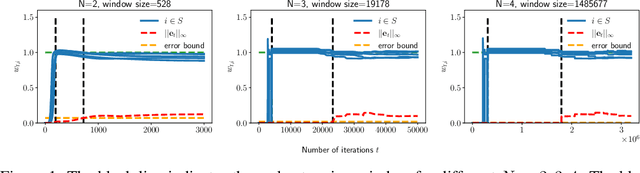
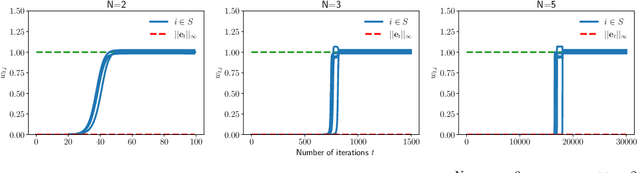
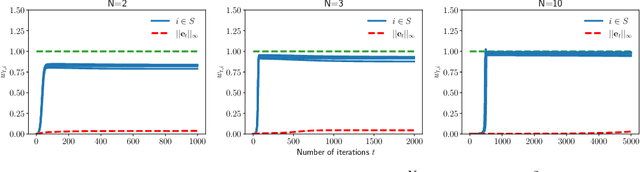
Abstract:In this paper, we study the implicit bias of gradient descent for sparse regression. We extend results on regression with quadratic parametrization, which amounts to depth-2 diagonal linear networks, to more general depth-N networks, under more realistic settings of noise and correlated designs. We show that early stopping is crucial for gradient descent to converge to a sparse model, a phenomenon that we call implicit sparse regularization. This result is in sharp contrast to known results for noiseless and uncorrelated-design cases. We characterize the impact of depth and early stopping and show that for a general depth parameter N, gradient descent with early stopping achieves minimax optimal sparse recovery with sufficiently small initialization and step size. In particular, we show that increasing depth enlarges the scale of working initialization and the early-stopping window, which leads to more stable gradient paths for sparse recovery.
Provable Compressed Sensing with Generative Priors via Langevin Dynamics
Feb 25, 2021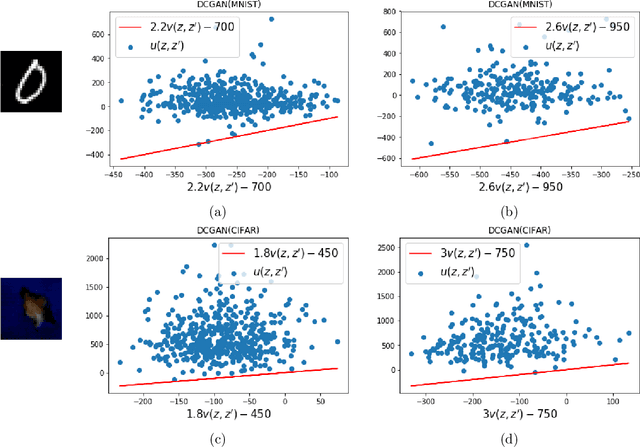


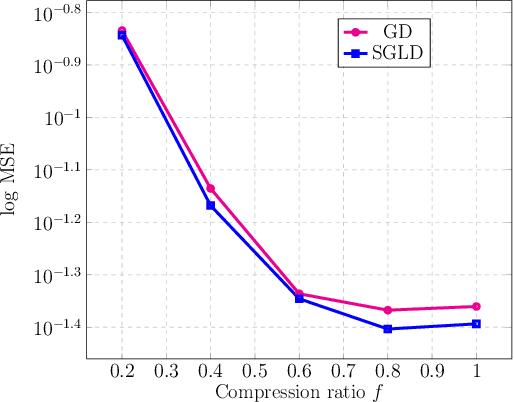
Abstract:Deep generative models have emerged as a powerful class of priors for signals in various inverse problems such as compressed sensing, phase retrieval and super-resolution. Here, we assume an unknown signal to lie in the range of some pre-trained generative model. A popular approach for signal recovery is via gradient descent in the low-dimensional latent space. While gradient descent has achieved good empirical performance, its theoretical behavior is not well understood. In this paper, we introduce the use of stochastic gradient Langevin dynamics (SGLD) for compressed sensing with a generative prior. Under mild assumptions on the generative model, we prove the convergence of SGLD to the true signal. We also demonstrate competitive empirical performance to standard gradient descent.
Active learning of deep surrogates for PDEs: Application to metasurface design
Aug 24, 2020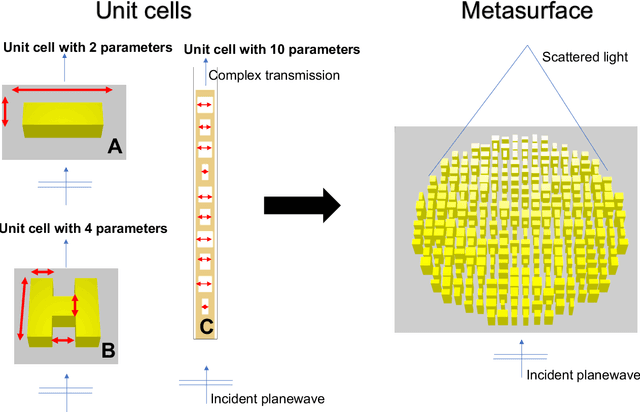
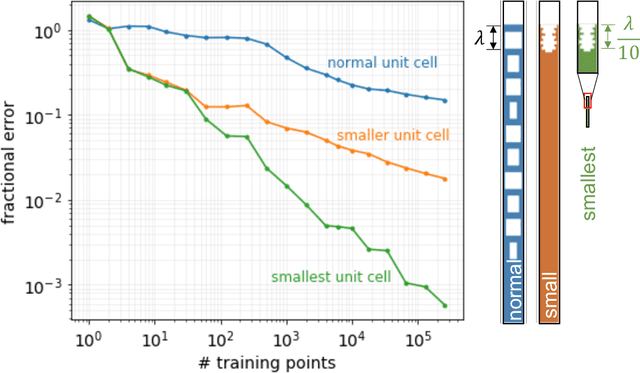
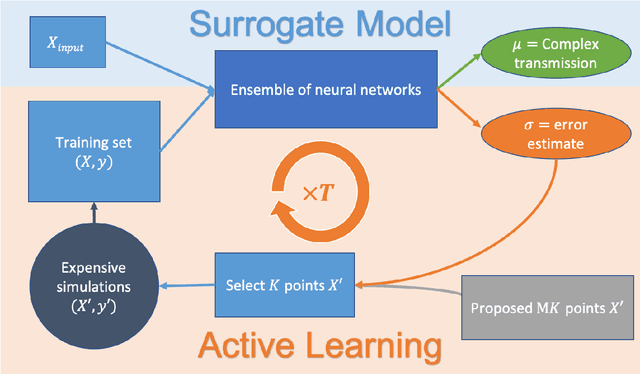
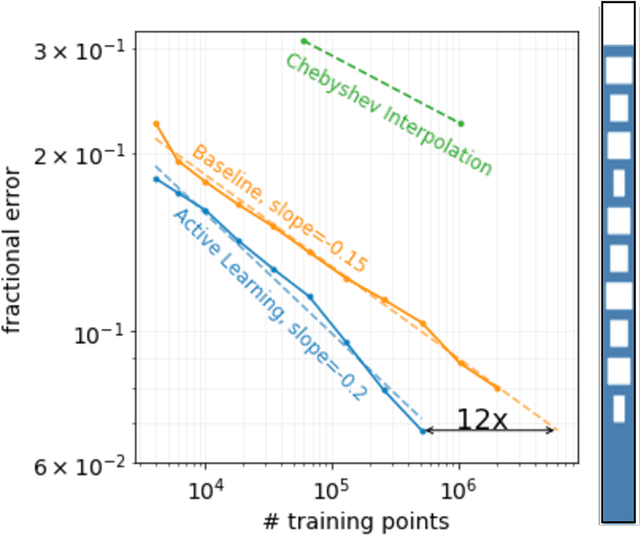
Abstract:Surrogate models for partial-differential equations are widely used in the design of meta-materials to rapidly evaluate the behavior of composable components. However, the training cost of accurate surrogates by machine learning can rapidly increase with the number of variables. For photonic-device models, we find that this training becomes especially challenging as design regions grow larger than the optical wavelength. We present an active learning algorithm that reduces the number of training points by more than an order of magnitude for a neural-network surrogate model of optical-surface components compared to random samples. Results show that the surrogate evaluation is over two orders of magnitude faster than a direct solve, and we demonstrate how this can be exploited to accelerate large-scale engineering optimization.
Learning Robust Models for e-Commerce Product Search
May 07, 2020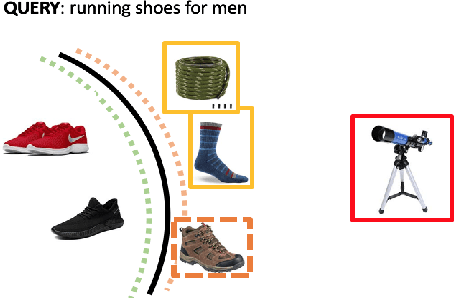
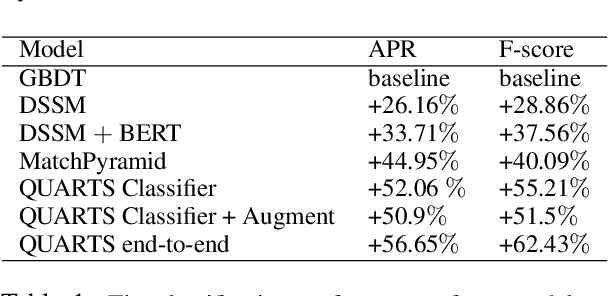
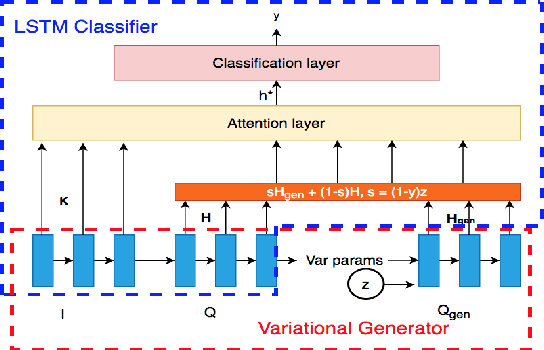

Abstract:Showing items that do not match search query intent degrades customer experience in e-commerce. These mismatches result from counterfactual biases of the ranking algorithms toward noisy behavioral signals such as clicks and purchases in the search logs. Mitigating the problem requires a large labeled dataset, which is expensive and time-consuming to obtain. In this paper, we develop a deep, end-to-end model that learns to effectively classify mismatches and to generate hard mismatched examples to improve the classifier. We train the model end-to-end by introducing a latent variable into the cross-entropy loss that alternates between using the real and generated samples. This not only makes the classifier more robust but also boosts the overall ranking performance. Our model achieves a relative gain compared to baselines by over 26% in F-score, and over 17% in Area Under PR curve. On live search traffic, our model gains significant improvement in multiple countries.
Benefits of Jointly Training Autoencoders: An Improved Neural Tangent Kernel Analysis
Nov 27, 2019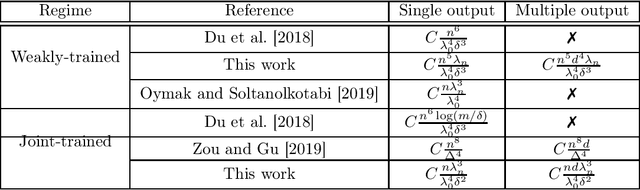
Abstract:A remarkable recent discovery in machine learning has been that deep neural networks can achieve impressive performance (in terms of both lower training error and higher generalization capacity) in the regime where they are massively over-parameterized. Consequently, over the last several months, the community has devoted growing interest in analyzing optimization and generalization properties of over-parameterized networks, and several breakthrough works have led to important theoretical progress. However, the majority of existing work only applies to supervised learning scenarios and hence are limited to settings such as classification and regression. In contrast, the role of over-parameterization in the unsupervised setting has gained far less attention. In this paper, we study the gradient dynamics of two-layer over-parameterized autoencoders with ReLU activation. We make very few assumptions about the given training dataset (other than mild non-degeneracy conditions). Starting from a randomly initialized autoencoder network, we rigorously prove the linear convergence of gradient descent in two learning regimes, namely: (i) the weakly-trained regime where only the encoder is trained, and (ii) the jointly-trained regime where both the encoder and the decoder are trained. Our results indicate the considerable benefits of joint training over weak training for finding global optima, achieving a dramatic decrease in the required level of over-parameterization. We also analyze the case of weight-tied autoencoders (which is a commonly used architectural choice in practical settings) and prove that in the over-parameterized setting, training such networks from randomly initialized points leads to certain unexpected degeneracies.
Autoencoders Learn Generative Linear Models
Jun 02, 2018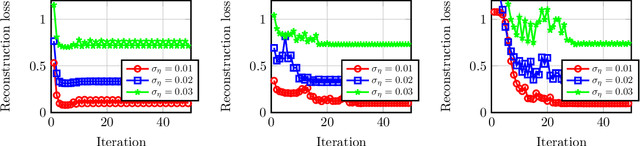
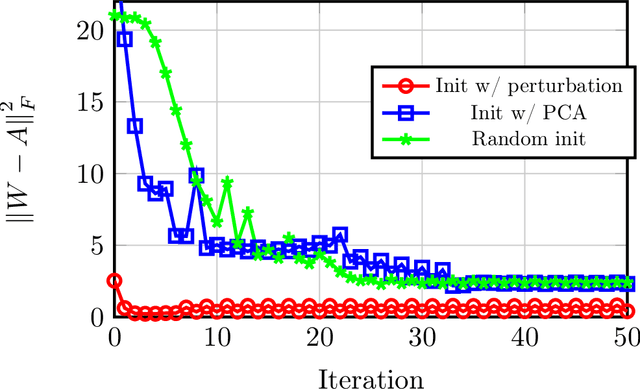
Abstract:Recent progress in learning theory has led to the emergence of provable algorithms for training certain families of neural networks. Under the assumption that the training data is sampled from a suitable generative model, the weights of the trained networks obtained by these algorithms recover (either exactly or approximately) the generative model parameters. However, the large majority of these results are only applicable to supervised learning architectures. In this paper, we complement this line of work by providing a series of results for unsupervised learning with neural networks. Specifically, we study the familiar setting of shallow autoencoder architectures with shared weights. We focus on three generative models for the data: (i) the mixture-of-gaussians model, (ii) the sparse coding model, and (iii) the non-negative sparsity model. All three models are widely studied in the machine learning literature. For each of these models, we rigorously prove that under suitable choices of hyperparameters, architectures, and initialization, the autoencoder weights learned by gradient descent % -based training can successfully recover the parameters of the corresponding model. To our knowledge, this is the first result that rigorously studies the dynamics of gradient descent for weight-sharing autoencoders. Our analysis can be viewed as theoretical evidence that shallow autoencoder modules indeed can be used as unsupervised feature training mechanisms for a wide range of datasets, and may shed insight on how to train larger stacked architectures with autoencoders as basic building blocks.
On Learning Sparsely Used Dictionaries from Incomplete Samples
Apr 24, 2018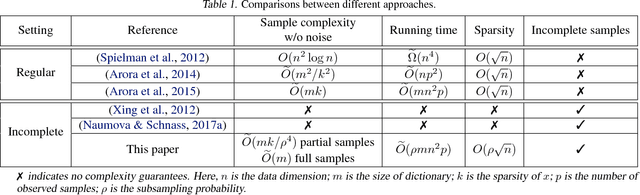
Abstract:Most existing algorithms for dictionary learning assume that all entries of the (high-dimensional) input data are fully observed. However, in several practical applications (such as hyper-spectral imaging or blood glucose monitoring), only an incomplete fraction of the data entries may be available. For incomplete settings, no provably correct and polynomial-time algorithm has been reported in the dictionary learning literature. In this paper, we provide provable approaches for learning - from incomplete samples - a family of dictionaries whose atoms have sufficiently "spread-out" mass. First, we propose a descent-style iterative algorithm that linearly converges to the true dictionary when provided a sufficiently coarse initial estimate. Second, we propose an initialization algorithm that utilizes a small number of extra fully observed samples to produce such a coarse initial estimate. Finally, we theoretically analyze their performance and provide asymptotic statistical and computational guarantees.
Provably Accurate Double-Sparse Coding
Dec 12, 2017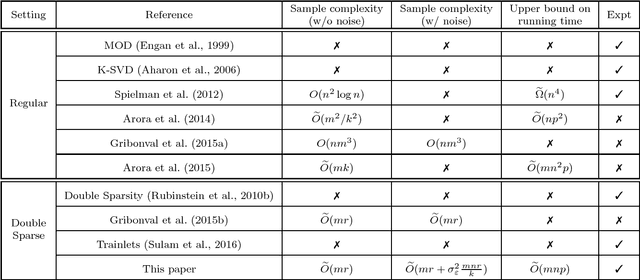
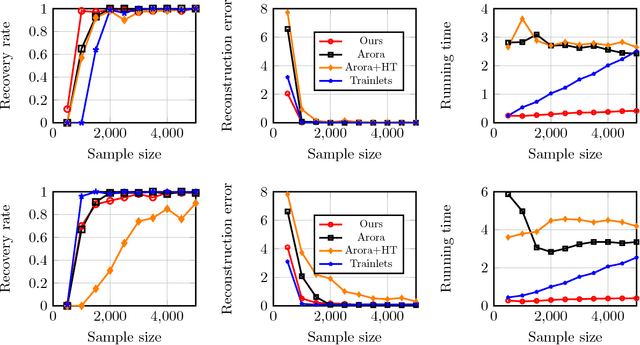
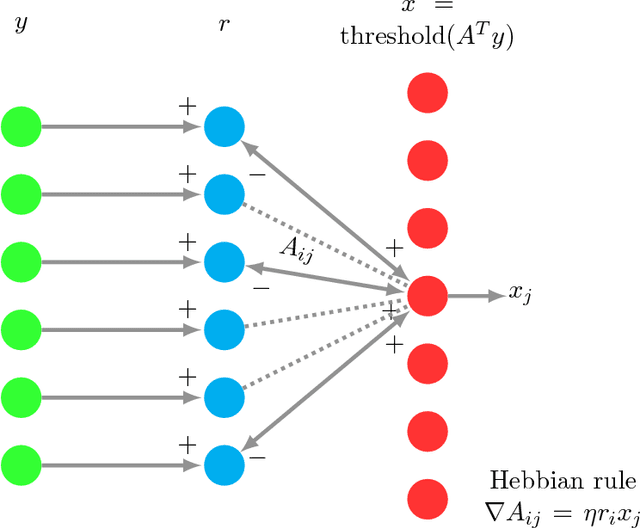
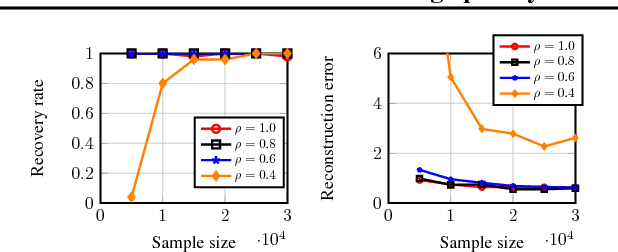
Abstract:Sparse coding is a crucial subroutine in algorithms for various signal processing, deep learning, and other machine learning applications. The central goal is to learn an overcomplete dictionary that can sparsely represent a given input dataset. However, a key challenge is that storage, transmission, and processing of the learned dictionary can be untenably high if the data dimension is high. In this paper, we consider the double-sparsity model introduced by Rubinstein et al. (2010b) where the dictionary itself is the product of a fixed, known basis and a data-adaptive sparse component. First, we introduce a simple algorithm for double-sparse coding that can be amenable to efficient implementation via neural architectures. Second, we theoretically analyze its performance and demonstrate asymptotic sample complexity and running time benefits over existing (provable) approaches for sparse coding. To our knowledge, our work introduces the first computationally efficient algorithm for double-sparse coding that enjoys rigorous statistical guarantees. Finally, we support our analysis via several numerical experiments on simulated data, confirming that our method can indeed be useful in problem sizes encountered in practical applications.
A Forward-Backward Approach for Visualizing Information Flow in Deep Networks
Nov 16, 2017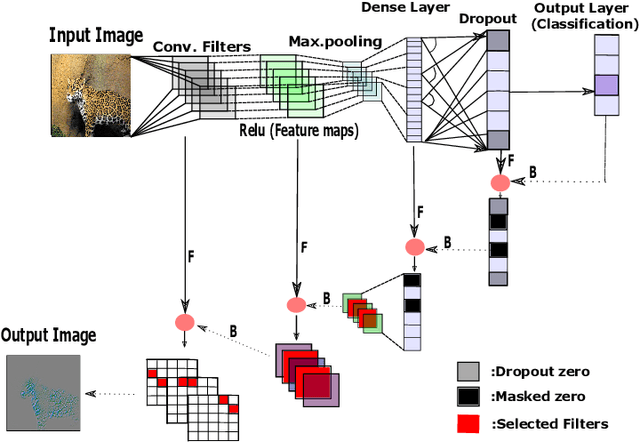

Abstract:We introduce a new, systematic framework for visualizing information flow in deep networks. Specifically, given any trained deep convolutional network model and a given test image, our method produces a compact support in the image domain that corresponds to a (high-resolution) feature that contributes to the given explanation. Our method is both computationally efficient as well as numerically robust. We present several preliminary numerical results that support the benefits of our framework over existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge