Distributional Off-policy Evaluation with Bellman Residual Minimization

We consider the problem of distributional off-policy evaluation which serves as the foundation of many distributional reinforcement learning (DRL) algorithms. In contrast to most existing works (that rely on supremum-extended statistical distances such as supremum-Wasserstein distance), we study the expectation-extended statistical distance for quantifying the distributional Bellman residuals and show that it can upper bound the expected error of estimating the return distribution. Based on this appealing property, by extending the framework of Bellman residual minimization to DRL, we propose a method called Energy Bellman Residual Minimizer (EBRM) to estimate the return distribution. We establish a finite-sample error bound for the EBRM estimator under the realizability assumption. Furthermore, we introduce a variant of our method based on a multi-step bootstrapping procedure to enable multi-step extension. By selecting an appropriate step level, we obtain a better error bound for this variant of EBRM compared to a single-step EBRM, under some non-realizability settings. Finally, we demonstrate the superior performance of our method through simulation studies, comparing with several existing methods.

Directed Cyclic Graph for Causal Discovery from Multivariate Functional Data

Discovering causal relationship using multivariate functional data has received a significant amount of attention very recently. In this article, we introduce a functional linear structural equation model for causal structure learning when the underlying graph involving the multivariate functions may have cycles. To enhance interpretability, our model involves a low-dimensional causal embedded space such that all the relevant causal information in the multivariate functional data is preserved in this lower-dimensional subspace. We prove that the proposed model is causally identifiable under standard assumptions that are often made in the causal discovery literature. To carry out inference of our model, we develop a fully Bayesian framework with suitable prior specifications and uncertainty quantification through posterior summaries. We illustrate the superior performance of our method over existing methods in terms of causal graph estimation through extensive simulation studies. We also demonstrate the proposed method using a brain EEG dataset.

Implicit Regularization for Group Sparsity

We study the implicit regularization of gradient descent towards structured sparsity via a novel neural reparameterization, which we call a diagonally grouped linear neural network. We show the following intriguing property of our reparameterization: gradient descent over the squared regression loss, without any explicit regularization, biases towards solutions with a group sparsity structure. In contrast to many existing works in understanding implicit regularization, we prove that our training trajectory cannot be simulated by mirror descent. We analyze the gradient dynamics of the corresponding regression problem in the general noise setting and obtain minimax-optimal error rates. Compared to existing bounds for implicit sparse regularization using diagonal linear networks, our analysis with the new reparameterization shows improved sample complexity. In the degenerate case of size-one groups, our approach gives rise to a new algorithm for sparse linear regression. Finally, we demonstrate the efficacy of our approach with several numerical experiments.

Extending the Use of MDL for High-Dimensional Problems: Variable Selection, Robust Fitting, and Additive Modeling

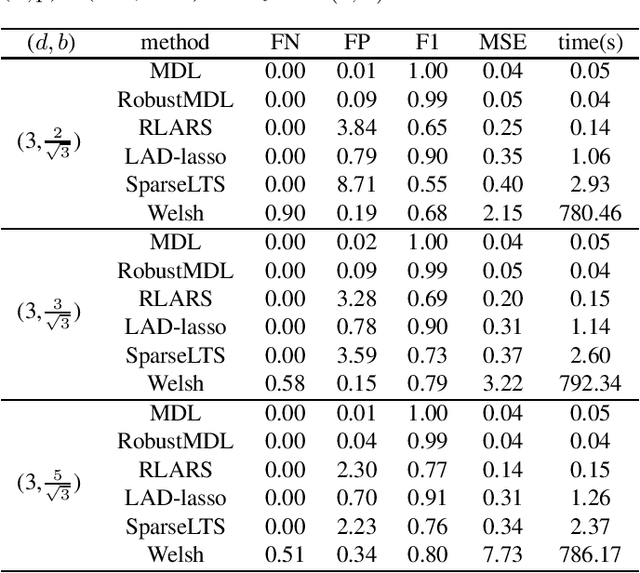
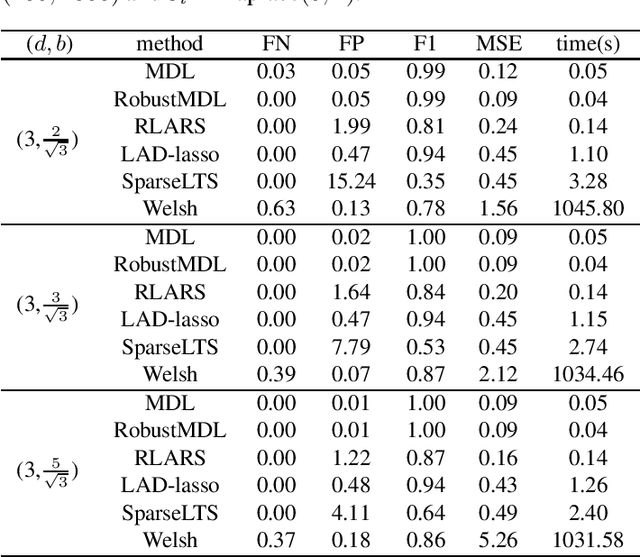
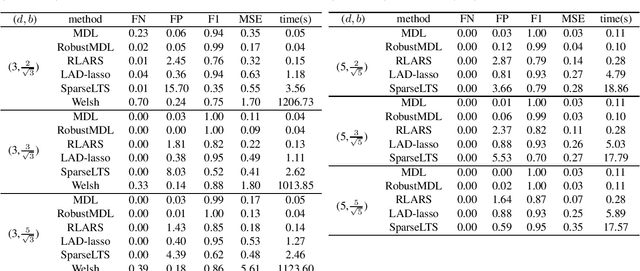
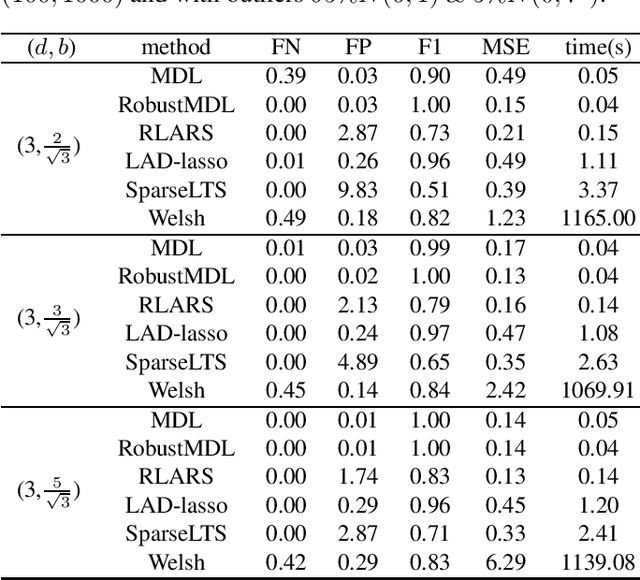
In the signal processing and statistics literature, the minimum description length (MDL) principle is a popular tool for choosing model complexity. Successful examples include signal denoising and variable selection in linear regression, for which the corresponding MDL solutions often enjoy consistent properties and produce very promising empirical results. This paper demonstrates that MDL can be extended naturally to the high-dimensional setting, where the number of predictors $p$ is larger than the number of observations $n$. It first considers the case of linear regression, then allows for outliers in the data, and lastly extends to the robust fitting of nonparametric additive models. Results from numerical experiments are presented to demonstrate the efficiency and effectiveness of the MDL approach.

Projected State-action Balancing Weights for Offline Reinforcement Learning

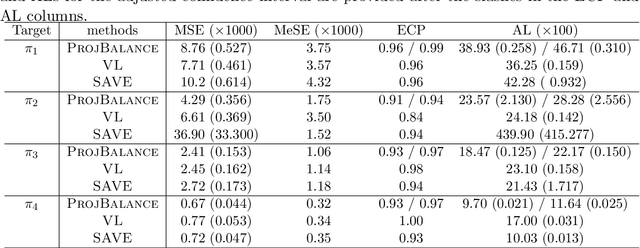
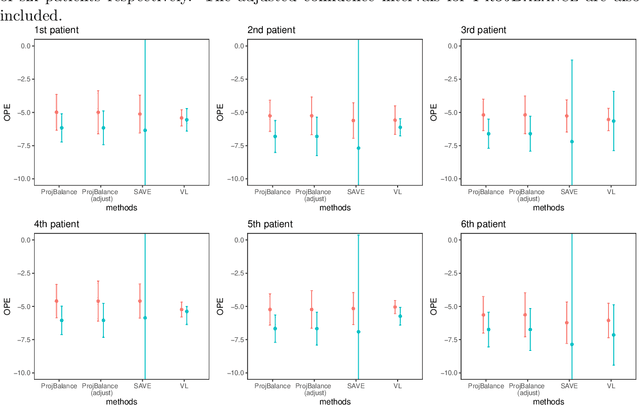
Offline policy evaluation (OPE) is considered a fundamental and challenging problem in reinforcement learning (RL). This paper focuses on the value estimation of a target policy based on pre-collected data generated from a possibly different policy, under the framework of infinite-horizon Markov decision processes. Motivated by the recently developed marginal importance sampling method in RL and the covariate balancing idea in causal inference, we propose a novel estimator with approximately projected state-action balancing weights for the policy value estimation. We obtain the convergence rate of these weights, and show that the proposed value estimator is semi-parametric efficient under technical conditions. In terms of asymptotics, our results scale with both the number of trajectories and the number of decision points at each trajectory. As such, consistency can still be achieved with a limited number of subjects when the number of decision points diverges. In addition, we make a first attempt towards characterizing the difficulty of OPE problems, which may be of independent interest. Numerical experiments demonstrate the promising performance of our proposed estimator.

Implicit Sparse Regularization: The Impact of Depth and Early Stopping

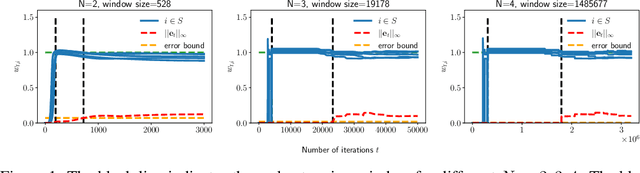
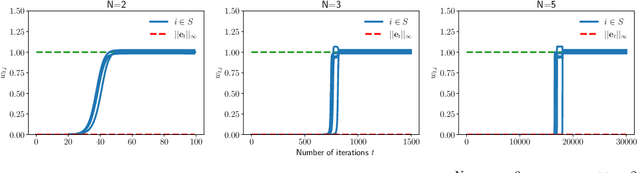
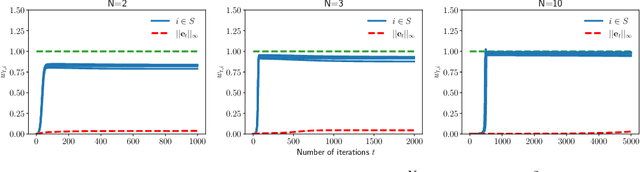
In this paper, we study the implicit bias of gradient descent for sparse regression. We extend results on regression with quadratic parametrization, which amounts to depth-2 diagonal linear networks, to more general depth-N networks, under more realistic settings of noise and correlated designs. We show that early stopping is crucial for gradient descent to converge to a sparse model, a phenomenon that we call implicit sparse regularization. This result is in sharp contrast to known results for noiseless and uncorrelated-design cases. We characterize the impact of depth and early stopping and show that for a general depth parameter N, gradient descent with early stopping achieves minimax optimal sparse recovery with sufficiently small initialization and step size. In particular, we show that increasing depth enlarges the scale of working initialization and the early-stopping window, which leads to more stable gradient paths for sparse recovery.

Matrix Completion with Model-free Weighting

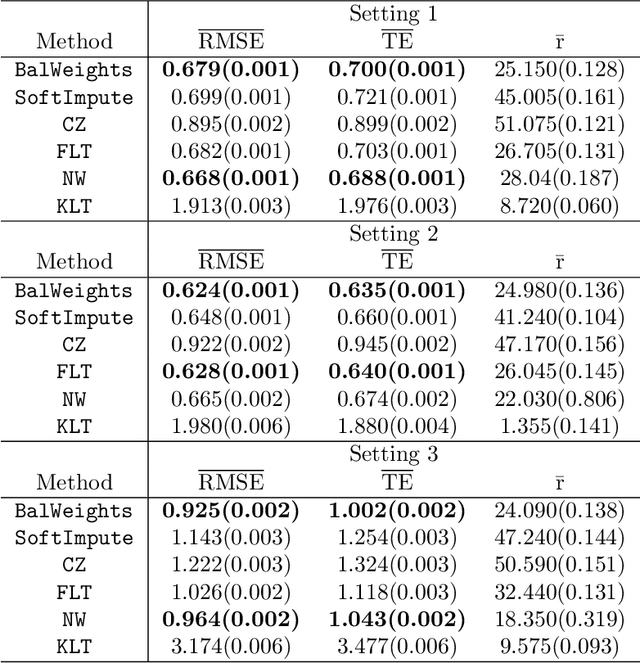
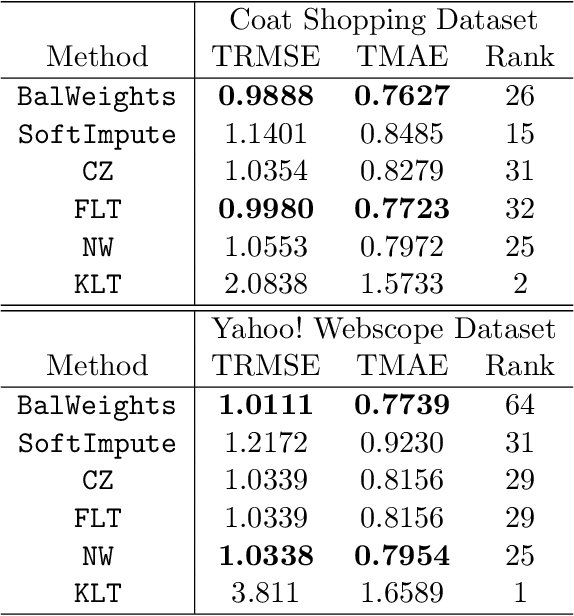
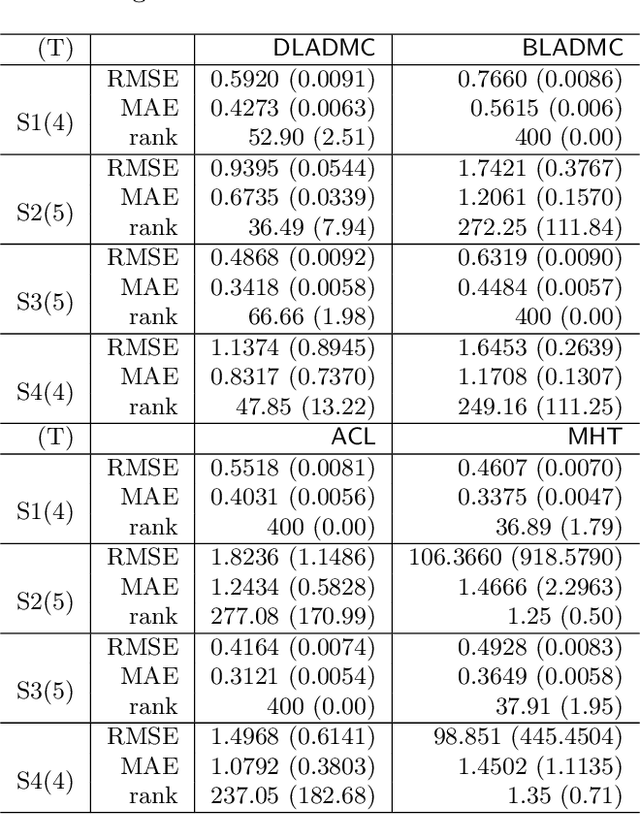
In this paper, we propose a novel method for matrix completion under general non-uniform missing structures. By controlling an upper bound of a novel balancing error, we construct weights that can actively adjust for the non-uniformity in the empirical risk without explicitly modeling the observation probabilities, and can be computed efficiently via convex optimization. The recovered matrix based on the proposed weighted empirical risk enjoys appealing theoretical guarantees. In particular, the proposed method achieves a stronger guarantee than existing work in terms of the scaling with respect to the observation probabilities, under asymptotically heterogeneous missing settings (where entry-wise observation probabilities can be of different orders). These settings can be regarded as a better theoretical model of missing patterns with highly varying probabilities. We also provide a new minimax lower bound under a class of heterogeneous settings. Numerical experiments are also provided to demonstrate the effectiveness of the proposed method.

CP Degeneracy in Tensor Regression

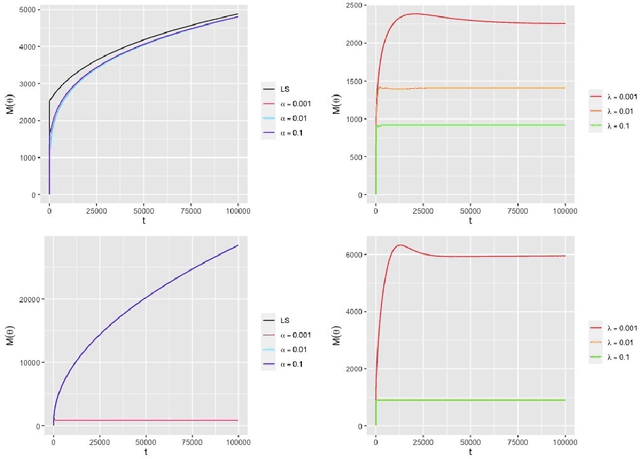
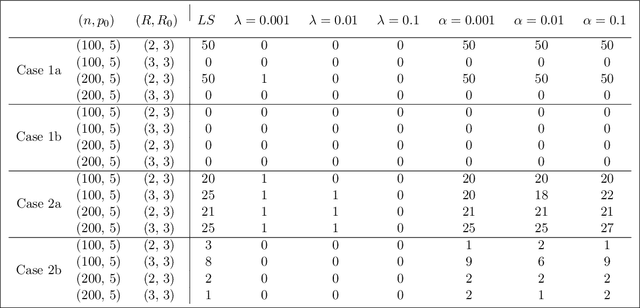
Tensor linear regression is an important and useful tool for analyzing tensor data. To deal with high dimensionality, CANDECOMP/PARAFAC (CP) low-rank constraints are often imposed on the coefficient tensor parameter in the (penalized) $M$-estimation. However, we show that the corresponding optimization may not be attainable, and when this happens, the estimator is not well-defined. This is closely related to a phenomenon, called CP degeneracy, in low-rank tensor approximation problems. In this article, we provide useful results of CP degeneracy in tensor regression problems. In addition, we provide a general penalized strategy as a solution to overcome CP degeneracy. The asymptotic properties of the resulting estimation are also studied. Numerical experiments are conducted to illustrate our findings.

Median Matrix Completion: from Embarrassment to Optimality

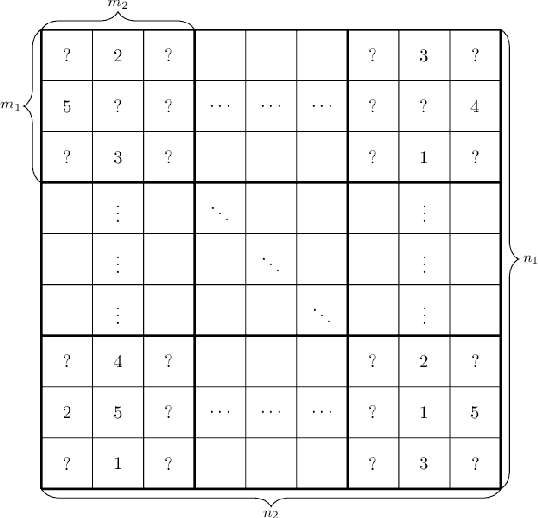
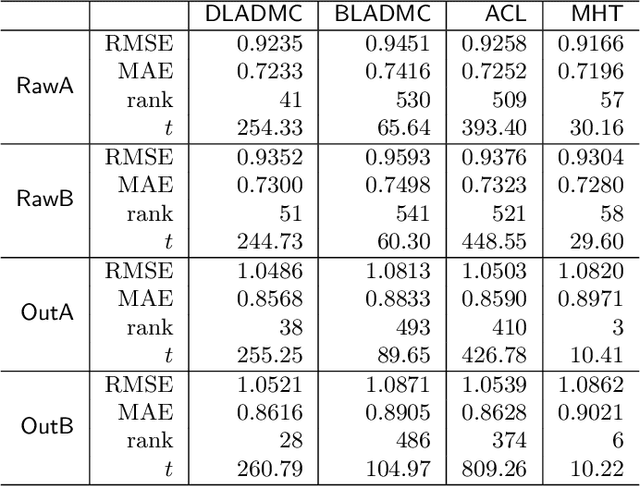
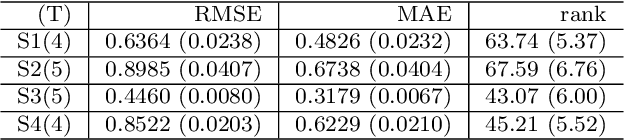
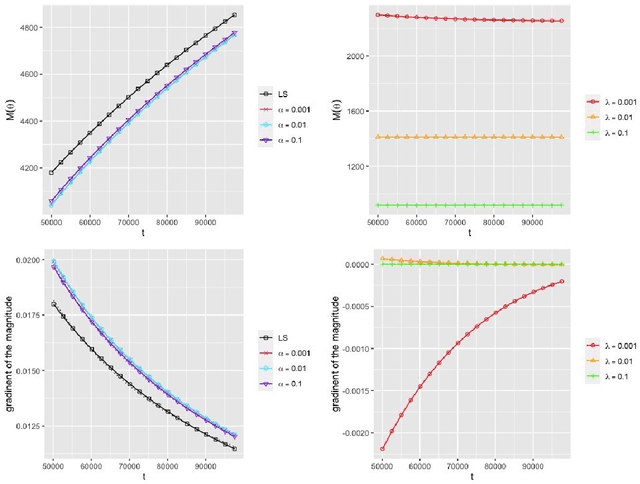
In this paper, we consider matrix completion with absolute deviation loss and obtain an estimator of the median matrix. Despite several appealing properties of median, the non-smooth absolute deviation loss leads to computational challenge for large-scale data sets which are increasingly common among matrix completion problems. A simple solution to large-scale problems is parallel computing. However, embarrassingly parallel fashion often leads to inefficient estimators. Based on the idea of pseudo data, we propose a novel refinement step, which turns such inefficient estimators into a rate (near-)optimal matrix completion procedure. The refined estimator is an approximation of a regularized least median estimator, and therefore not an ordinary regularized empirical risk estimator. This leads to a non-standard analysis of asymptotic behaviors. Empirical results are also provided to confirm the effectiveness of the proposed method.

Benefits of Jointly Training Autoencoders: An Improved Neural Tangent Kernel Analysis

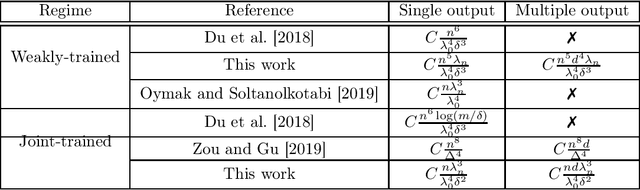
A remarkable recent discovery in machine learning has been that deep neural networks can achieve impressive performance (in terms of both lower training error and higher generalization capacity) in the regime where they are massively over-parameterized. Consequently, over the last several months, the community has devoted growing interest in analyzing optimization and generalization properties of over-parameterized networks, and several breakthrough works have led to important theoretical progress. However, the majority of existing work only applies to supervised learning scenarios and hence are limited to settings such as classification and regression. In contrast, the role of over-parameterization in the unsupervised setting has gained far less attention. In this paper, we study the gradient dynamics of two-layer over-parameterized autoencoders with ReLU activation. We make very few assumptions about the given training dataset (other than mild non-degeneracy conditions). Starting from a randomly initialized autoencoder network, we rigorously prove the linear convergence of gradient descent in two learning regimes, namely: (i) the weakly-trained regime where only the encoder is trained, and (ii) the jointly-trained regime where both the encoder and the decoder are trained. Our results indicate the considerable benefits of joint training over weak training for finding global optima, achieving a dramatic decrease in the required level of over-parameterization. We also analyze the case of weight-tied autoencoders (which is a commonly used architectural choice in practical settings) and prove that in the over-parameterized setting, training such networks from randomly initialized points leads to certain unexpected degeneracies.