Diffeomorphic interpolation for efficient persistence-based topological optimization

Topological Data Analysis (TDA) provides a pipeline to extract quantitative topological descriptors from structured objects. This enables the definition of topological loss functions, which assert to what extent a given object exhibits some topological properties. These losses can then be used to perform topological optimizationvia gradient descent routines. While theoretically sounded, topological optimization faces an important challenge: gradients tend to be extremely sparse, in the sense that the loss function typically depends on only very few coordinates of the input object, yielding dramatically slow optimization schemes in practice.Focusing on the central case of topological optimization for point clouds, we propose in this work to overcome this limitation using diffeomorphic interpolation, turning sparse gradients into smooth vector fields defined on the whole space, with quantifiable Lipschitz constants. In particular, we show that our approach combines efficiently with subsampling techniques routinely used in TDA, as the diffeomorphism derived from the gradient computed on a subsample can be used to update the coordinates of the full input object, allowing us to perform topological optimization on point clouds at an unprecedented scale. Finally, we also showcase the relevance of our approach for black-box autoencoder (AE) regularization, where we aim at enforcing topological priors on the latent spaces associated to fixed, pre-trained, black-box AE models, and where we show thatlearning a diffeomorphic flow can be done once and then re-applied to new data in linear time (while vanilla topological optimization has to be re-run from scratch). Moreover, reverting the flow allows us to generate data by sampling the topologically-optimized latent space directly, yielding better interpretability of the model.

Topological Node2vec: Enhanced Graph Embedding via Persistent Homology

Node2vec is a graph embedding method that learns a vector representation for each node of a weighted graph while seeking to preserve relative proximity and global structure. Numerical experiments suggest Node2vec struggles to recreate the topology of the input graph. To resolve this we introduce a topological loss term to be added to the training loss of Node2vec which tries to align the persistence diagram (PD) of the resulting embedding as closely as possible to that of the input graph. Following results in computational optimal transport, we carefully adapt entropic regularization to PD metrics, allowing us to measure the discrepancy between PDs in a differentiable way. Our modified loss function can then be minimized through gradient descent to reconstruct both the geometry and the topology of the input graph. We showcase the benefits of this approach using demonstrative synthetic examples.

MAGDiff: Covariate Data Set Shift Detection via Activation Graphs of Deep Neural Networks

Despite their successful application to a variety of tasks, neural networks remain limited, like other machine learning methods, by their sensitivity to shifts in the data: their performance can be severely impacted by differences in distribution between the data on which they were trained and that on which they are deployed. In this article, we propose a new family of representations, called MAGDiff, that we extract from any given neural network classifier and that allows for efficient covariate data shift detection without the need to train a new model dedicated to this task. These representations are computed by comparing the activation graphs of the neural network for samples belonging to the training distribution and to the target distribution, and yield powerful data- and task-adapted statistics for the two-sample tests commonly used for data set shift detection. We demonstrate this empirically by measuring the statistical powers of two-sample Kolmogorov-Smirnov (KS) tests on several different data sets and shift types, and showing that our novel representations induce significant improvements over a state-of-the-art baseline relying on the network output.

RipsNet: a general architecture for fast and robust estimation of the persistent homology of point clouds

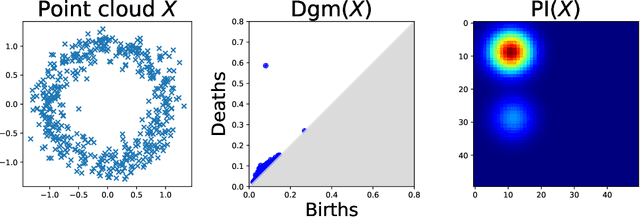
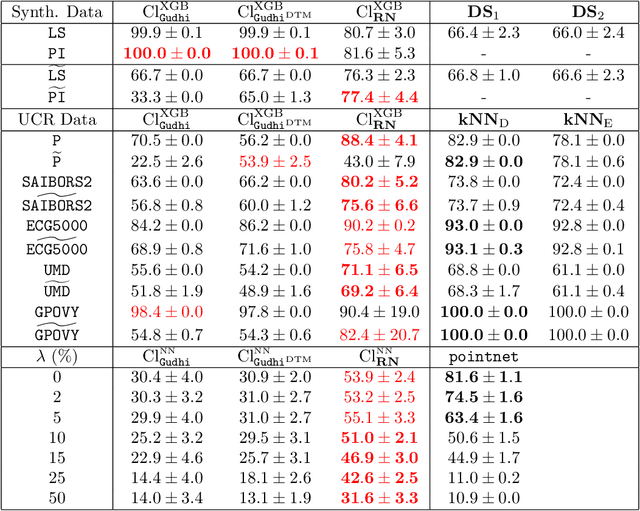
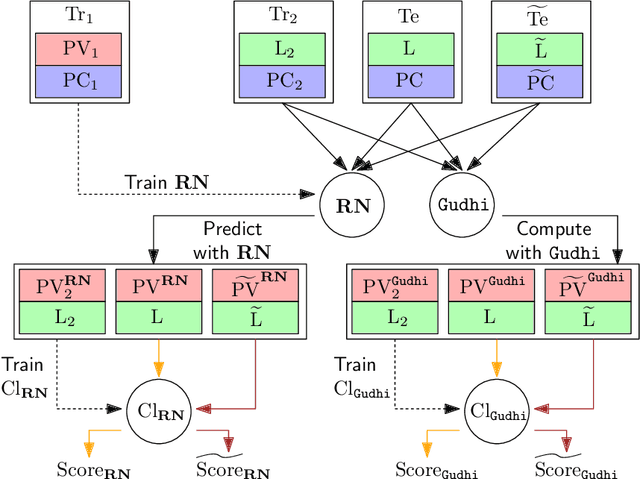
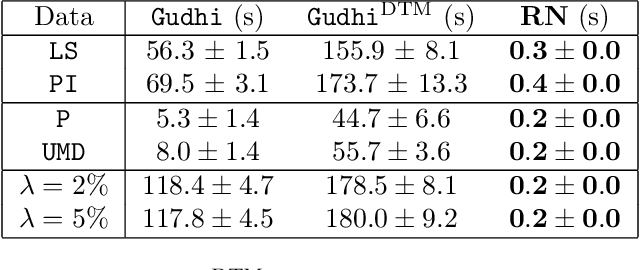
The use of topological descriptors in modern machine learning applications, such as Persistence Diagrams (PDs) arising from Topological Data Analysis (TDA), has shown great potential in various domains. However, their practical use in applications is often hindered by two major limitations: the computational complexity required to compute such descriptors exactly, and their sensitivity to even low-level proportions of outliers. In this work, we propose to bypass these two burdens in a data-driven setting by entrusting the estimation of (vectorization of) PDs built on top of point clouds to a neural network architecture that we call RipsNet. Once trained on a given data set, RipsNet can estimate topological descriptors on test data very efficiently with generalization capacity. Furthermore, we prove that RipsNet is robust to input perturbations in terms of the 1-Wasserstein distance, a major improvement over the standard computation of PDs that only enjoys Hausdorff stability, yielding RipsNet to substantially outperform exactly-computed PDs in noisy settings. We showcase the use of RipsNet on both synthetic and real-world data. Our open-source implementation is publicly available at https://github.com/hensel-f/ripsnet and will be included in the Gudhi library.

An Homogeneous Unbalanced Regularized Optimal Transport model with applications to Optimal Transport with Boundary

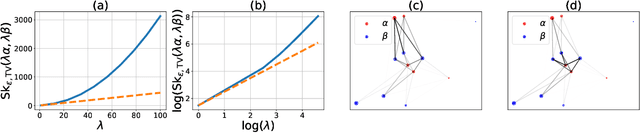
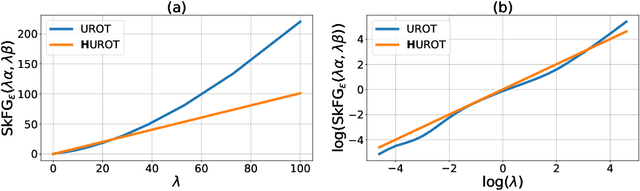
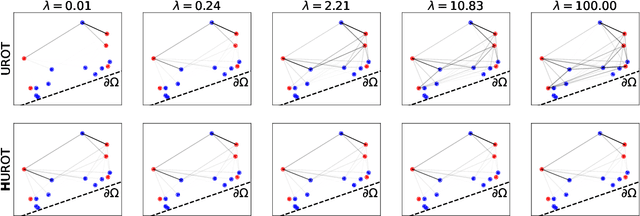
This work studies how the introduction of the entropic regularization term in unbalanced Optimal Transport (OT) models may alter their homogeneity with respect to the input measures. We observe that in common settings (including balanced OT and unbalanced OT with Kullback-Leibler divergence to the marginals), although the optimal transport cost itself is not homogeneous, optimal transport plans and the so-called Sinkhorn divergences are indeed homogeneous. However, homogeneity does not hold in more general Unbalanced Regularized Optimal Transport (UROT) models, for instance those using the Total Variation as divergence to the marginals. We propose to modify the entropic regularization term to retrieve an UROT model that is homogeneous while preserving most properties of the standard UROT model. We showcase the importance of using our Homogeneous UROT (HUROT) model when it comes to regularize Optimal Transport with Boundary, a transportation model involving a spatially varying divergence to the marginals for which the standard (inhomogeneous) UROT model would yield inappropriate behavior.

A Gradient Sampling Algorithm for Stratified Maps with Applications to Topological Data Analysis

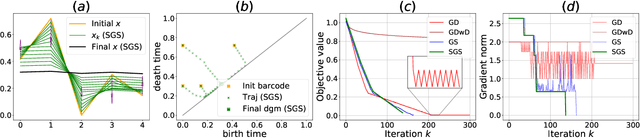
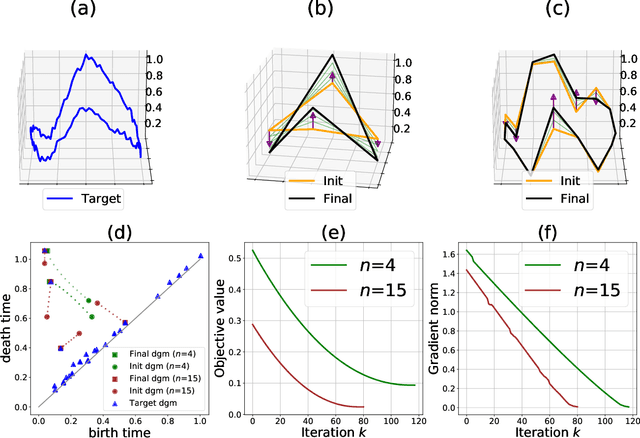
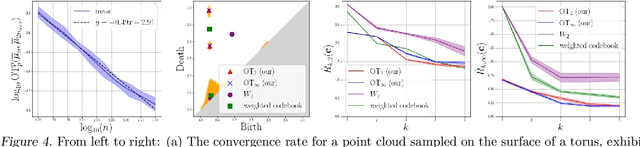
We introduce a novel gradient descent algorithm extending the well-known Gradient Sampling methodology to the class of stratifiably smooth objective functions, which are defined as locally Lipschitz functions that are smooth on some regular pieces-called the strata-of the ambient Euclidean space. For this class of functions, our algorithm achieves a sub-linear convergence rate. We then apply our method to objective functions based on the (extended) persistent homology map computed over lower-star filters, which is a central tool of Topological Data Analysis. For this, we propose an efficient exploration of the corresponding stratification by using the Cayley graph of the permutation group. Finally, we provide benchmark and novel topological optimization problems, in order to demonstrate the utility and applicability of our framework.

Estimation and Quantization of Expected Persistence Diagrams

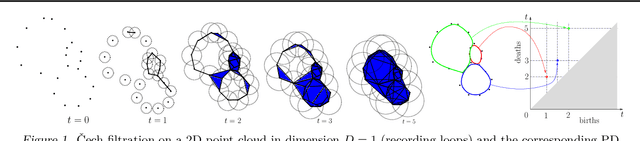
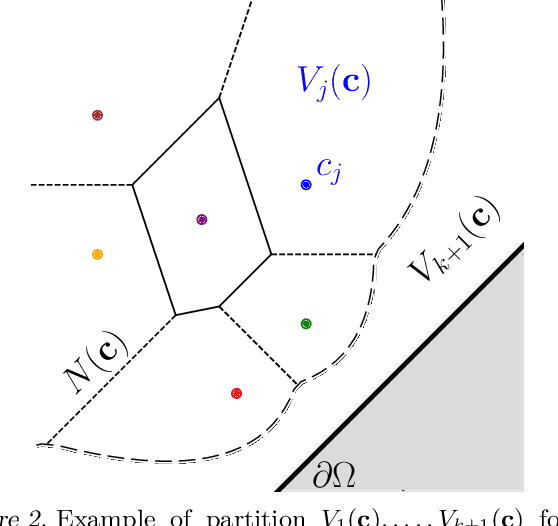
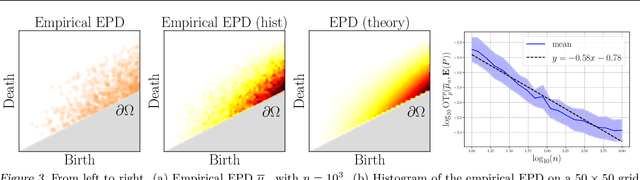
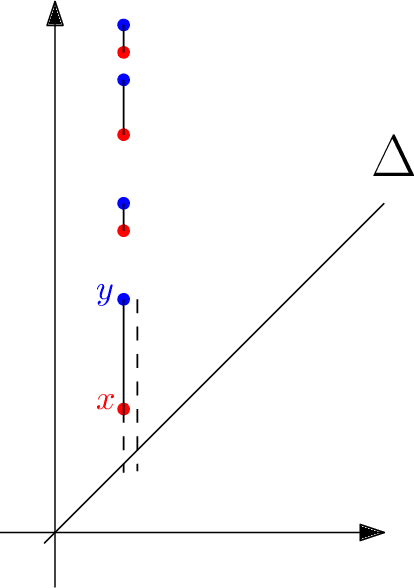
Persistence diagrams (PDs) are the most common descriptors used to encode the topology of structured data appearing in challenging learning tasks; think e.g. of graphs, time series or point clouds sampled close to a manifold. Given random objects and the corresponding distribution of PDs, one may want to build a statistical summary-such as a mean-of these random PDs, which is however not a trivial task as the natural geometry of the space of PDs is not linear. In this article, we study two such summaries, the Expected Persistence Diagram (EPD), and its quantization. The EPD is a measure supported on R 2 , which may be approximated by its empirical counterpart. We prove that this estimator is optimal from a minimax standpoint on a large class of models with a parametric rate of convergence. The empirical EPD is simple and efficient to compute, but possibly has a very large support, hindering its use in practice. To overcome this issue, we propose an algorithm to compute a quantization of the empirical EPD, a measure with small support which is shown to approximate with near-optimal rates a quantization of the theoretical EPD.

Topological Uncertainty: Monitoring trained neural networks through persistence of activation graphs

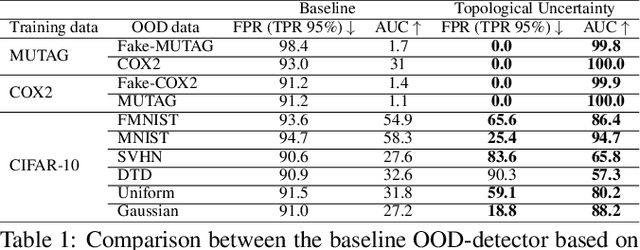
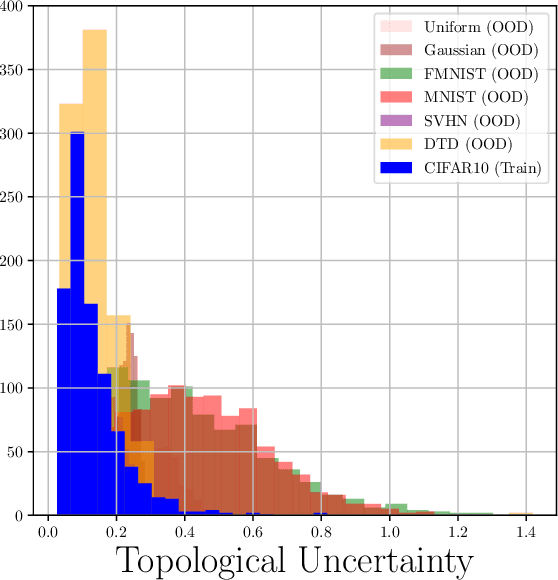
Although neural networks are capable of reaching astonishing performances on a wide variety of contexts, properly training networks on complicated tasks requires expertise and can be expensive from a computational perspective. In industrial applications, data coming from an open-world setting might widely differ from the benchmark datasets on which a network was trained. Being able to monitor the presence of such variations without retraining the network is of crucial importance. In this article, we develop a method to monitor trained neural networks based on the topological properties of their activation graphs. To each new observation, we assign a Topological Uncertainty, a score that aims to assess the reliability of the predictions by investigating the whole network instead of its final layer only, as typically done by practitioners. Our approach entirely works at a post-training level and does not require any assumption on the network architecture, optimization scheme, nor the use of data augmentation or auxiliary datasets; and can be faithfully applied on a large range of network architectures and data types. We showcase experimentally the potential of Topological Uncertainty in the context of trained network selection, Out-Of-Distribution detection, and shift-detection, both on synthetic and real datasets of images and graphs.

PersLay: A Simple and Versatile Neural Network Layer for Persistence Diagrams

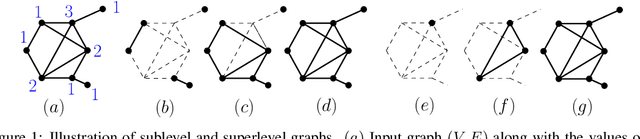
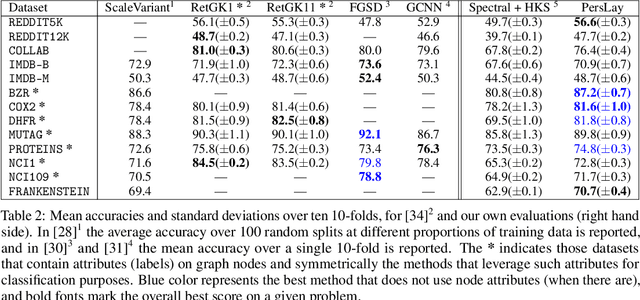
Persistence diagrams, a key descriptor from Topological Data Analysis, encode and summarize all sorts of topological features and have already proved pivotal in many different applications of data science. But persistence diagrams are weakly structured and therefore constitute a difficult input for most Machine Learning techniques. To address this concern several vectorization methods have been put forward that embed persistence diagrams into either finite-dimensional Euclidean spaces or implicit Hilbert spaces with kernels. But finite-dimensional embeddings are prone to miss a lot of information about persistence diagrams, while kernel methods require the full computation of the kernel matrix. We introduce PersLay: a simple, highly modular layer of learning architecture for persistence diagrams that allows to exploit the full capacities of neural networks on topological information from any dataset. This layer encompasses most of the vectorization methods of the literature. We illustrate its strengths on challenging classification problems on dynamical systems orbit or real-life graph data, with results improving or comparable to the state-of-the-art. In order to exploit topological information from graph data, we show how graph structures can be encoded in the so-called extended persistence diagrams computed with the heat kernel signatures of the graphs.

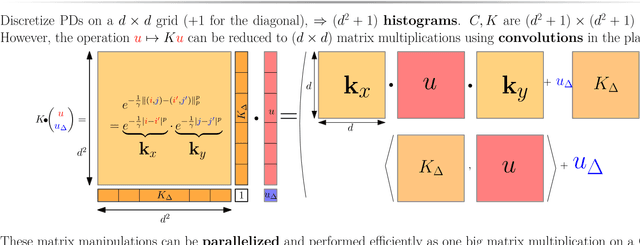
Large Scale computation of Means and Clusters for Persistence Diagrams using Optimal Transport

Persistence diagrams (PDs) are now routinely used to summarize the underlying topology of sophisticated data encountered in challenging learning problems. Despite several appealing properties, integrating PDs in learning pipelines can be challenging because their natural geometry is not Hilbertian. In particular, algorithms to average a family of PDs have only been considered recently and are known to be computationally prohibitive. We propose in this article a tractable framework to carry out fundamental tasks on PDs, namely evaluating distances, computing barycenters and carrying out clustering. This framework builds upon a formulation of PD metrics as optimal transport (OT) problems, for which recent computational advances, in particular entropic regularization and its convolutional formulation on regular grids, can all be leveraged to provide efficient and (GPU) scalable computations. We demonstrate the efficiency of our approach by carrying out clustering on PDs at scales never seen before in the literature.