Demographic parity in regression and classification within the unawareness framework

This paper explores the theoretical foundations of fair regression under the constraint of demographic parity within the unawareness framework, where disparate treatment is prohibited, extending existing results where such treatment is permitted. Specifically, we aim to characterize the optimal fair regression function when minimizing the quadratic loss. Our results reveal that this function is given by the solution to a barycenter problem with optimal transport costs. Additionally, we study the connection between optimal fair cost-sensitive classification, and optimal fair regression. We demonstrate that nestedness of the decision sets of the classifiers is both necessary and sufficient to establish a form of equivalence between classification and regression. Under this nestedness assumption, the optimal classifiers can be derived by applying thresholds to the optimal fair regression function; conversely, the optimal fair regression function is characterized by the family of cost-sensitive classifiers.

Minimax estimation of discontinuous optimal transport maps: The semi-discrete case

We consider the problem of estimating the optimal transport map between two probability distributions, $P$ and $Q$ in $\mathbb R^d$, on the basis of i.i.d. samples. All existing statistical analyses of this problem require the assumption that the transport map is Lipschitz, a strong requirement that, in particular, excludes any examples where the transport map is discontinuous. As a first step towards developing estimation procedures for discontinuous maps, we consider the important special case where the data distribution $Q$ is a discrete measure supported on a finite number of points in $\mathbb R^d$. We study a computationally efficient estimator initially proposed by Pooladian and Niles-Weed (2021), based on entropic optimal transport, and show in the semi-discrete setting that it converges at the minimax-optimal rate $n^{-1/2}$, independent of dimension. Other standard map estimation techniques both lack finite-sample guarantees in this setting and provably suffer from the curse of dimensionality. We confirm these results in numerical experiments, and provide experiments for other settings, not covered by our theory, which indicate that the entropic estimator is a promising methodology for other discontinuous transport map estimation problems.

Optimal transport map estimation in general function spaces

We consider the problem of estimating the optimal transport map between a (fixed) source distribution $P$ and an unknown target distribution $Q$, based on samples from $Q$. The estimation of such optimal transport maps has become increasingly relevant in modern statistical applications, such as generative modeling. At present, estimation rates are only known in a few settings (e.g. when $P$ and $Q$ have densities bounded above and below and when the transport map lies in a H\"older class), which are often not reflected in practice. We present a unified methodology for obtaining rates of estimation of optimal transport maps in general function spaces. Our assumptions are significantly weaker than those appearing in the literature: we require only that the source measure $P$ satisfies a Poincar\'e inequality and that the optimal map be the gradient of a smooth convex function that lies in a space whose metric entropy can be controlled. As a special case, we recover known estimation rates for bounded densities and H\"older transport maps, but also obtain nearly sharp results in many settings not covered by prior work. For example, we provide the first statistical rates of estimation when $P$ is the normal distribution and the transport map is given by an infinite-width shallow neural network.

Estimation and Quantization of Expected Persistence Diagrams

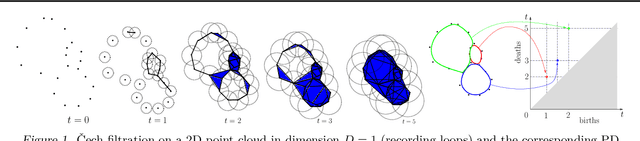
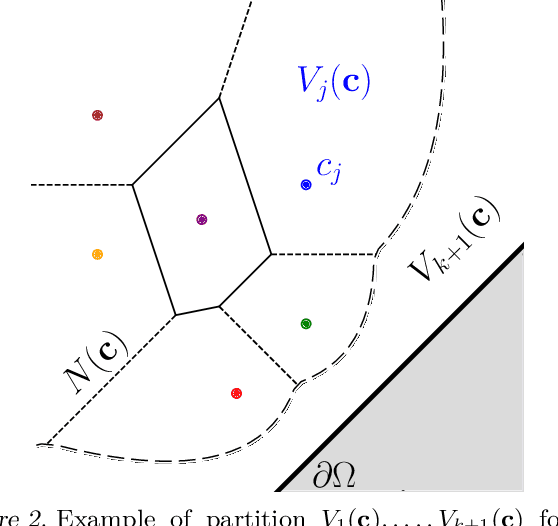
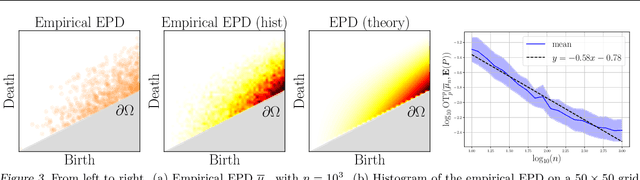
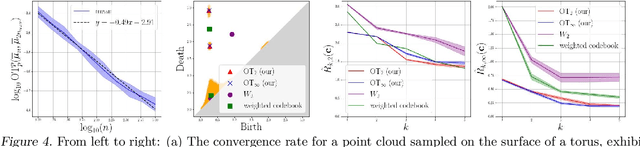
Persistence diagrams (PDs) are the most common descriptors used to encode the topology of structured data appearing in challenging learning tasks; think e.g. of graphs, time series or point clouds sampled close to a manifold. Given random objects and the corresponding distribution of PDs, one may want to build a statistical summary-such as a mean-of these random PDs, which is however not a trivial task as the natural geometry of the space of PDs is not linear. In this article, we study two such summaries, the Expected Persistence Diagram (EPD), and its quantization. The EPD is a measure supported on R 2 , which may be approximated by its empirical counterpart. We prove that this estimator is optimal from a minimax standpoint on a large class of models with a parametric rate of convergence. The empirical EPD is simple and efficient to compute, but possibly has a very large support, hindering its use in practice. To overcome this issue, we propose an algorithm to compute a quantization of the empirical EPD, a measure with small support which is shown to approximate with near-optimal rates a quantization of the theoretical EPD.