Differentiable Mapper For Topological Optimization Of Data Representation

Unsupervised data representation and visualization using tools from topology is an active and growing field of Topological Data Analysis (TDA) and data science. Its most prominent line of work is based on the so-called Mapper graph, which is a combinatorial graph whose topological structures (connected components, branches, loops) are in correspondence with those of the data itself. While highly generic and applicable, its use has been hampered so far by the manual tuning of its many parameters-among these, a crucial one is the so-called filter: it is a continuous function whose variations on the data set are the main ingredient for both building the Mapper representation and assessing the presence and sizes of its topological structures. However, while a few parameter tuning methods have already been investigated for the other Mapper parameters (i.e., resolution, gain, clustering), there is currently no method for tuning the filter itself. In this work, we build on a recently proposed optimization framework incorporating topology to provide the first filter optimization scheme for Mapper graphs. In order to achieve this, we propose a relaxed and more general version of the Mapper graph, whose convergence properties are investigated. Finally, we demonstrate the usefulness of our approach by optimizing Mapper graph representations on several datasets, and showcasing the superiority of the optimized representation over arbitrary ones.

A Framework for Fast and Stable Representations of Multiparameter Persistent Homology Decompositions

Topological data analysis (TDA) is an area of data science that focuses on using invariants from algebraic topology to provide multiscale shape descriptors for geometric data sets such as point clouds. One of the most important such descriptors is {\em persistent homology}, which encodes the change in shape as a filtration parameter changes; a typical parameter is the feature scale. For many data sets, it is useful to simultaneously vary multiple filtration parameters, for example feature scale and density. While the theoretical properties of single parameter persistent homology are well understood, less is known about the multiparameter case. In particular, a central question is the problem of representing multiparameter persistent homology by elements of a vector space for integration with standard machine learning algorithms. Existing approaches to this problem either ignore most of the multiparameter information to reduce to the one-parameter case or are heuristic and potentially unstable in the face of noise. In this article, we introduce a new general representation framework that leverages recent results on {\em decompositions} of multiparameter persistent homology. This framework is rich in information, fast to compute, and encompasses previous approaches. Moreover, we establish theoretical stability guarantees under this framework as well as efficient algorithms for practical computation, making this framework an applicable and versatile tool for analyzing geometric and point cloud data. We validate our stability results and algorithms with numerical experiments that demonstrate statistical convergence, prediction accuracy, and fast running times on several real data sets.

Stable Vectorization of Multiparameter Persistent Homology using Signed Barcodes as Measures

Persistent homology (PH) provides topological descriptors for geometric data, such as weighted graphs, which are interpretable, stable to perturbations, and invariant under, e.g., relabeling. Most applications of PH focus on the one-parameter case -- where the descriptors summarize the changes in topology of data as it is filtered by a single quantity of interest -- and there is now a wide array of methods enabling the use of one-parameter PH descriptors in data science, which rely on the stable vectorization of these descriptors as elements of a Hilbert space. Although the multiparameter PH (MPH) of data that is filtered by several quantities of interest encodes much richer information than its one-parameter counterpart, the scarceness of stability results for MPH descriptors has so far limited the available options for the stable vectorization of MPH. In this paper, we aim to bring together the best of both worlds by showing how the interpretation of signed barcodes -- a recent family of MPH descriptors -- as signed measures leads to natural extensions of vectorization strategies from one parameter to multiple parameters. The resulting feature vectors are easy to define and to compute, and provably stable. While, as a proof of concept, we focus on simple choices of signed barcodes and vectorizations, we already see notable performance improvements when comparing our feature vectors to state-of-the-art topology-based methods on various types of data.

MAGDiff: Covariate Data Set Shift Detection via Activation Graphs of Deep Neural Networks

Despite their successful application to a variety of tasks, neural networks remain limited, like other machine learning methods, by their sensitivity to shifts in the data: their performance can be severely impacted by differences in distribution between the data on which they were trained and that on which they are deployed. In this article, we propose a new family of representations, called MAGDiff, that we extract from any given neural network classifier and that allows for efficient covariate data shift detection without the need to train a new model dedicated to this task. These representations are computed by comparing the activation graphs of the neural network for samples belonging to the training distribution and to the target distribution, and yield powerful data- and task-adapted statistics for the two-sample tests commonly used for data set shift detection. We demonstrate this empirically by measuring the statistical powers of two-sample Kolmogorov-Smirnov (KS) tests on several different data sets and shift types, and showing that our novel representations induce significant improvements over a state-of-the-art baseline relying on the network output.

RipsNet: a general architecture for fast and robust estimation of the persistent homology of point clouds

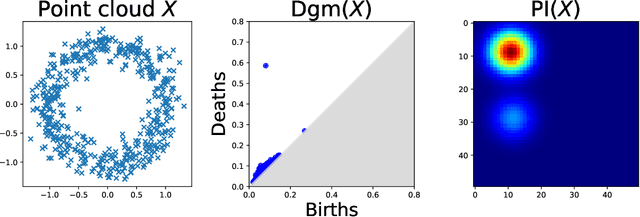
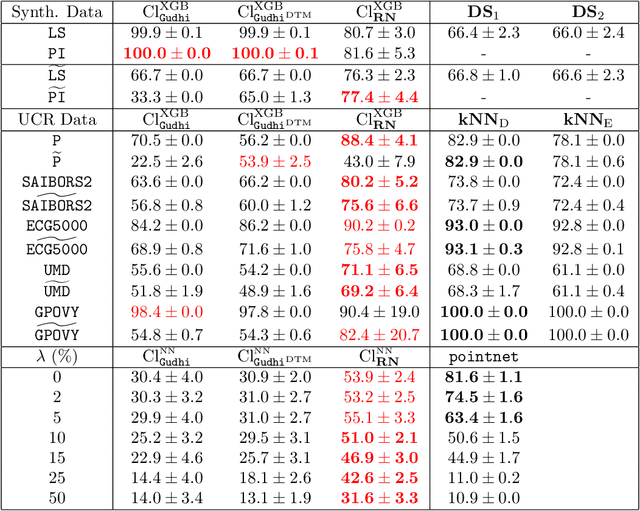
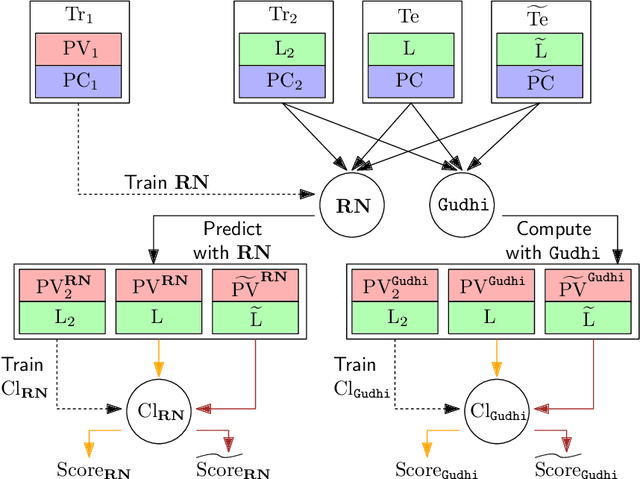
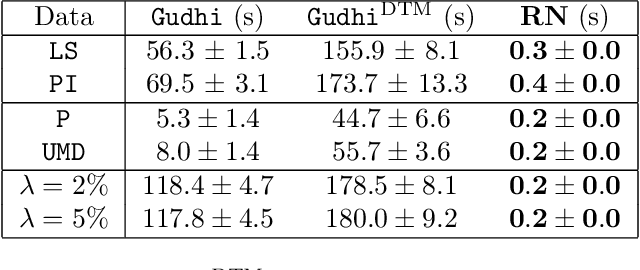
The use of topological descriptors in modern machine learning applications, such as Persistence Diagrams (PDs) arising from Topological Data Analysis (TDA), has shown great potential in various domains. However, their practical use in applications is often hindered by two major limitations: the computational complexity required to compute such descriptors exactly, and their sensitivity to even low-level proportions of outliers. In this work, we propose to bypass these two burdens in a data-driven setting by entrusting the estimation of (vectorization of) PDs built on top of point clouds to a neural network architecture that we call RipsNet. Once trained on a given data set, RipsNet can estimate topological descriptors on test data very efficiently with generalization capacity. Furthermore, we prove that RipsNet is robust to input perturbations in terms of the 1-Wasserstein distance, a major improvement over the standard computation of PDs that only enjoys Hausdorff stability, yielding RipsNet to substantially outperform exactly-computed PDs in noisy settings. We showcase the use of RipsNet on both synthetic and real-world data. Our open-source implementation is publicly available at https://github.com/hensel-f/ripsnet and will be included in the Gudhi library.

A Gradient Sampling Algorithm for Stratified Maps with Applications to Topological Data Analysis

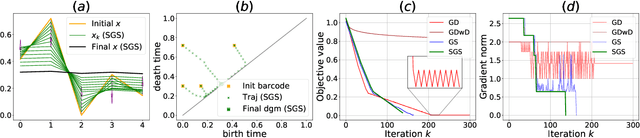
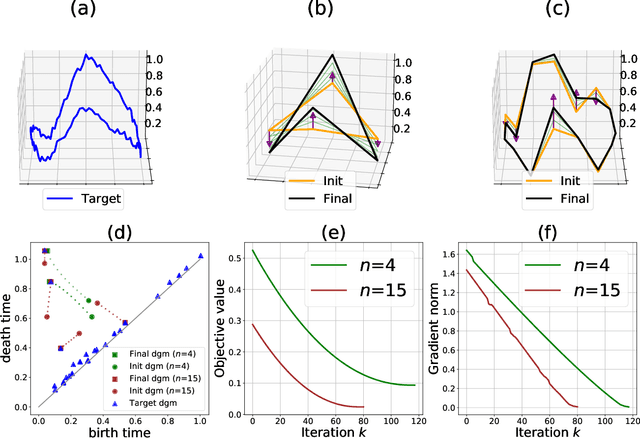
We introduce a novel gradient descent algorithm extending the well-known Gradient Sampling methodology to the class of stratifiably smooth objective functions, which are defined as locally Lipschitz functions that are smooth on some regular pieces-called the strata-of the ambient Euclidean space. For this class of functions, our algorithm achieves a sub-linear convergence rate. We then apply our method to objective functions based on the (extended) persistent homology map computed over lower-star filters, which is a central tool of Topological Data Analysis. For this, we propose an efficient exploration of the corresponding stratification by using the Cayley graph of the permutation group. Finally, we provide benchmark and novel topological optimization problems, in order to demonstrate the utility and applicability of our framework.

Approximation of Reeb spaces with Mappers and Applications to Stochastic Filters

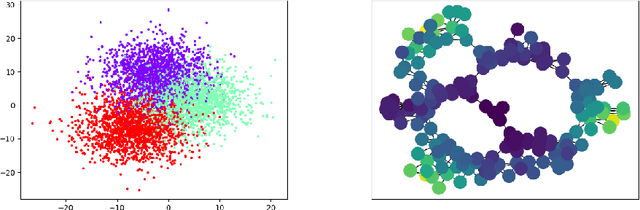
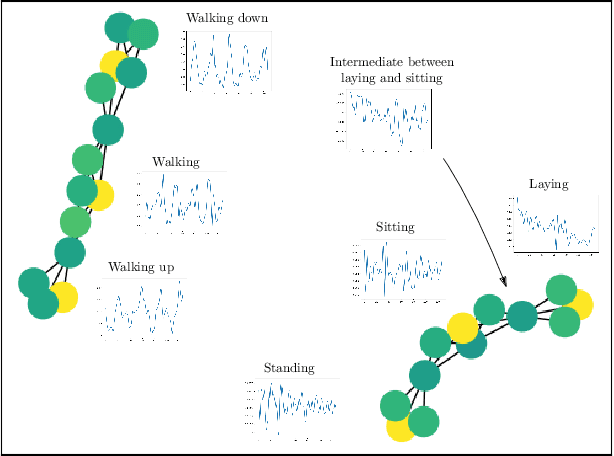
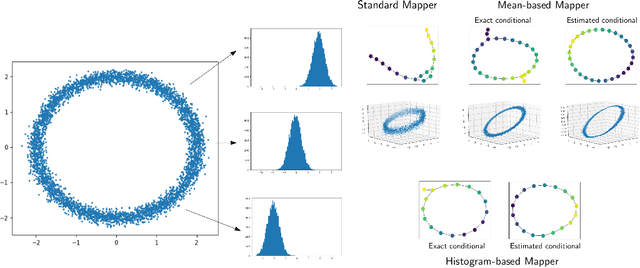
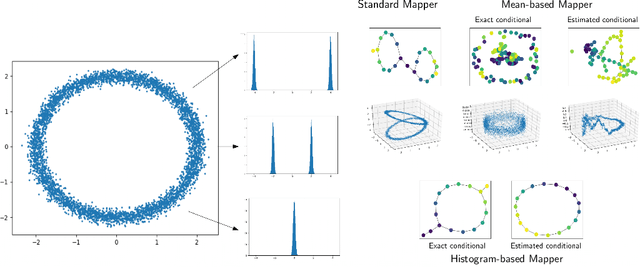
Reeb spaces, as well as their discretized versions called Mappers, are common descriptors used in Topological Data Analysis, with plenty of applications in various fields of science, such as computational biology and data visualization, among others. The stability and quantification of the rate of convergence of the Mapper to the Reeb space has been studied a lot in recent works~\cite{Brown2019, Carriere2018a, Carriere2018, Munch2016}, focusing on the case where a scalar-valued filter is used for the computation of Mapper. On the other hand, much less is known in the multivariate case, where the domain of the filter is in $\mathbb R^d$ instead of $\mathbb R$. The only available result in this setting~\cite{Munch2016} only works for topological spaces and cannot be used as is for finite metric spaces representing data, such as point clouds and distance matrices. In this article, we present an approximation result for the Reeb space in the multivariate case using a Mapper-based estimator, which is a slight modification of the usual Mapper construction. Moreover, our approximation is stated with respect to a pseudometric that is an extension of the usual {\em interleaving distance} between persistence modules~\cite{Chazal2016}. Finally, we apply our results to the case where the filter function used to compute the Mapper is estimated from the data. We provide applications of this setting in statistics and machine learning and probability for different kinds of target filters, as well as numerical experiments that demonstrate the relevance of our approach.

PersLay: A Simple and Versatile Neural Network Layer for Persistence Diagrams

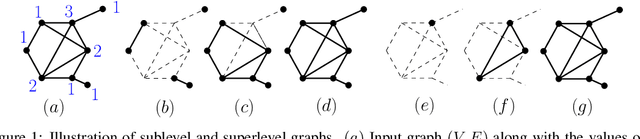
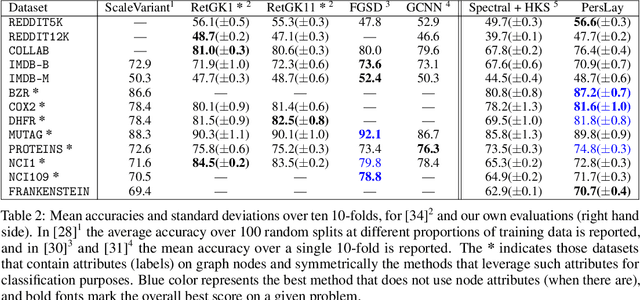
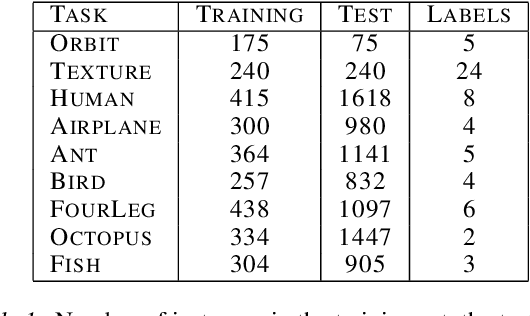
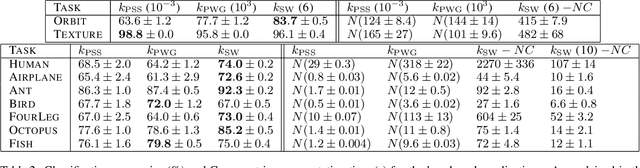
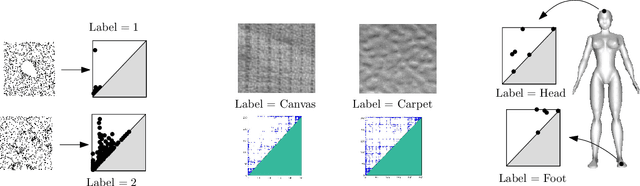
Persistence diagrams, a key descriptor from Topological Data Analysis, encode and summarize all sorts of topological features and have already proved pivotal in many different applications of data science. But persistence diagrams are weakly structured and therefore constitute a difficult input for most Machine Learning techniques. To address this concern several vectorization methods have been put forward that embed persistence diagrams into either finite-dimensional Euclidean spaces or implicit Hilbert spaces with kernels. But finite-dimensional embeddings are prone to miss a lot of information about persistence diagrams, while kernel methods require the full computation of the kernel matrix. We introduce PersLay: a simple, highly modular layer of learning architecture for persistence diagrams that allows to exploit the full capacities of neural networks on topological information from any dataset. This layer encompasses most of the vectorization methods of the literature. We illustrate its strengths on challenging classification problems on dynamical systems orbit or real-life graph data, with results improving or comparable to the state-of-the-art. In order to exploit topological information from graph data, we show how graph structures can be encoded in the so-called extended persistence diagrams computed with the heat kernel signatures of the graphs.

Sliced Wasserstein Kernel for Persistence Diagrams

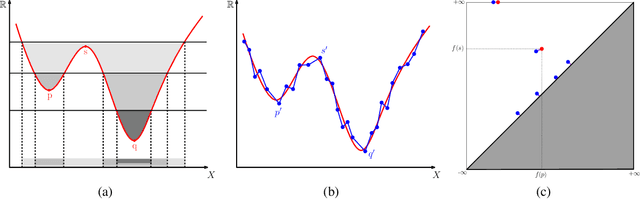
Persistence diagrams (PDs) play a key role in topological data analysis (TDA), in which they are routinely used to describe topological properties of complicated shapes. PDs enjoy strong stability properties and have proven their utility in various learning contexts. They do not, however, live in a space naturally endowed with a Hilbert structure and are usually compared with specific distances, such as the bottleneck distance. To incorporate PDs in a learning pipeline, several kernels have been proposed for PDs with a strong emphasis on the stability of the RKHS distance w.r.t. perturbations of the PDs. In this article, we use the Sliced Wasserstein approximation SW of the Wasserstein distance to define a new kernel for PDs, which is not only provably stable but also provably discriminative (depending on the number of points in the PDs) w.r.t. the Wasserstein distance $d_1$ between PDs. We also demonstrate its practicality, by developing an approximation technique to reduce kernel computation time, and show that our proposal compares favorably to existing kernels for PDs on several benchmarks.