Topological Analysis for Detecting Anomalies (TADA) in Time Series

This paper introduces new methodology based on the field of Topological Data Analysis for detecting anomalies in multivariate time series, that aims to detect global changes in the dependency structure between channels. The proposed approach is lean enough to handle large scale datasets, and extensive numerical experiments back the intuition that it is more suitable for detecting global changes of correlation structures than existing methods. Some theoretical guarantees for quantization algorithms based on dependent time sequences are also provided.

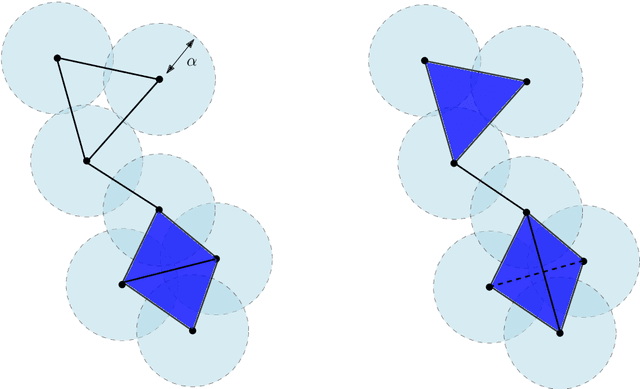
Choosing the parameter of the Fermat distance: navigating geometry and noise

The Fermat distance has been recently established as a useful tool for machine learning tasks when a natural distance is not directly available to the practitioner or to improve the results given by Euclidean distances by exploding the geometrical and statistical properties of the dataset. This distance depends on a parameter $\alpha$ that greatly impacts the performance of subsequent tasks. Ideally, the value of $\alpha$ should be large enough to navigate the geometric intricacies inherent to the problem. At the same, it should remain restrained enough to sidestep any deleterious ramifications stemming from noise during the process of distance estimation. We study both theoretically and through simulations how to select this parameter.

MAGDiff: Covariate Data Set Shift Detection via Activation Graphs of Deep Neural Networks

Despite their successful application to a variety of tasks, neural networks remain limited, like other machine learning methods, by their sensitivity to shifts in the data: their performance can be severely impacted by differences in distribution between the data on which they were trained and that on which they are deployed. In this article, we propose a new family of representations, called MAGDiff, that we extract from any given neural network classifier and that allows for efficient covariate data shift detection without the need to train a new model dedicated to this task. These representations are computed by comparing the activation graphs of the neural network for samples belonging to the training distribution and to the target distribution, and yield powerful data- and task-adapted statistics for the two-sample tests commonly used for data set shift detection. We demonstrate this empirically by measuring the statistical powers of two-sample Kolmogorov-Smirnov (KS) tests on several different data sets and shift types, and showing that our novel representations induce significant improvements over a state-of-the-art baseline relying on the network output.

Topological phase estimation method for reparameterized periodic functions

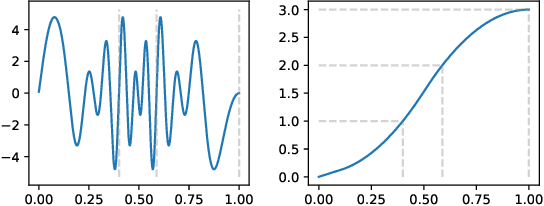
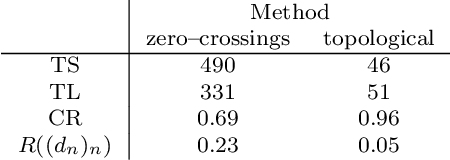
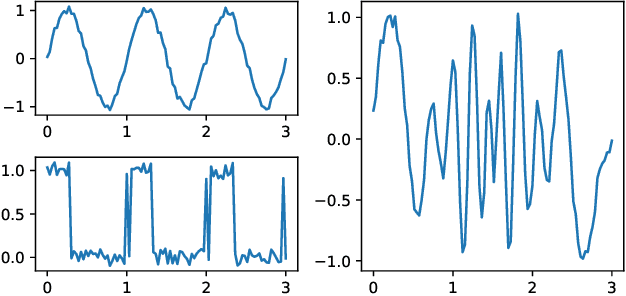
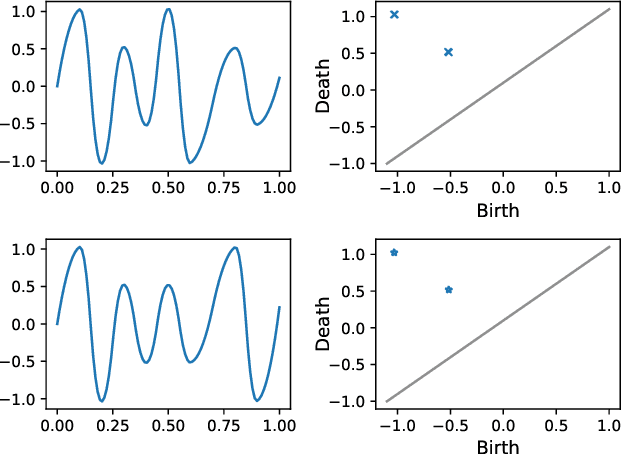
We consider a signal composed of several periods of a periodic function, of which we observe a noisy reparametrisation. The phase estimation problem consists of finding that reparametrisation, and, in particular, the number of observed periods. Existing methods are well-suited to the setting where the periodic function is known, or at least, simple. We consider the case when it is unknown and we propose an estimation method based on the shape of the signal. We use the persistent homology of sublevel sets of the signal to capture the temporal structure of its local extrema. We infer the number of periods in the signal by counting points in the persistence diagram and their multiplicities. Using the estimated number of periods, we construct an estimator of the reparametrisation. It is based on counting the number of sufficiently prominent local minima in the signal. This work is motivated by a vehicle positioning problem, on which we evaluated the proposed method.

RipsNet: a general architecture for fast and robust estimation of the persistent homology of point clouds

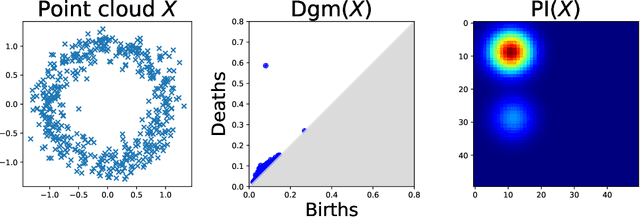
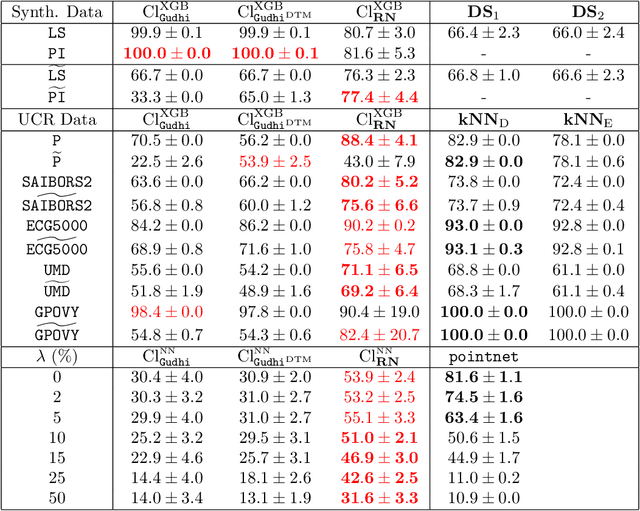
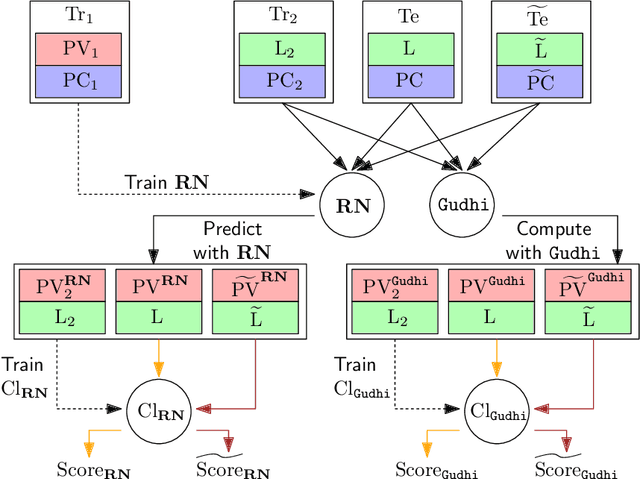
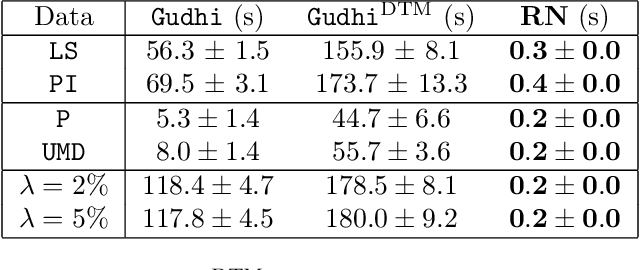
The use of topological descriptors in modern machine learning applications, such as Persistence Diagrams (PDs) arising from Topological Data Analysis (TDA), has shown great potential in various domains. However, their practical use in applications is often hindered by two major limitations: the computational complexity required to compute such descriptors exactly, and their sensitivity to even low-level proportions of outliers. In this work, we propose to bypass these two burdens in a data-driven setting by entrusting the estimation of (vectorization of) PDs built on top of point clouds to a neural network architecture that we call RipsNet. Once trained on a given data set, RipsNet can estimate topological descriptors on test data very efficiently with generalization capacity. Furthermore, we prove that RipsNet is robust to input perturbations in terms of the 1-Wasserstein distance, a major improvement over the standard computation of PDs that only enjoys Hausdorff stability, yielding RipsNet to substantially outperform exactly-computed PDs in noisy settings. We showcase the use of RipsNet on both synthetic and real-world data. Our open-source implementation is publicly available at https://github.com/hensel-f/ripsnet and will be included in the Gudhi library.

Topological Uncertainty: Monitoring trained neural networks through persistence of activation graphs

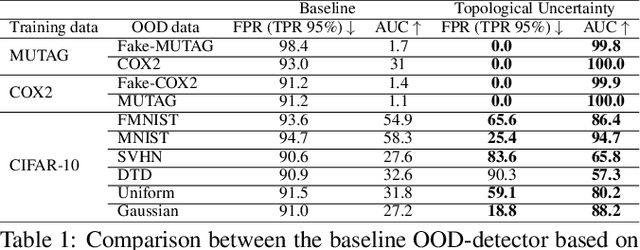
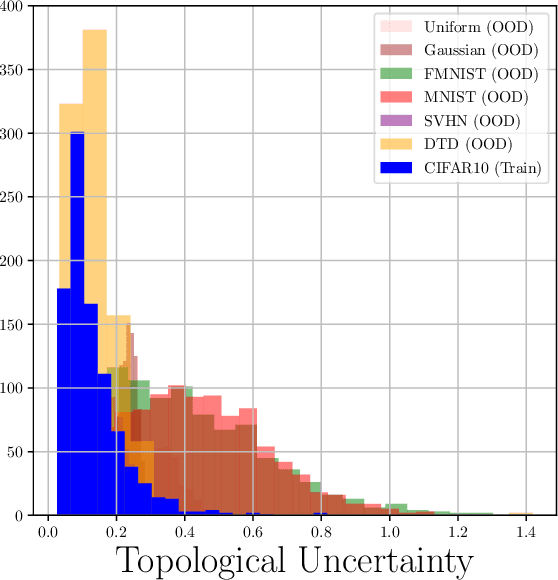
Although neural networks are capable of reaching astonishing performances on a wide variety of contexts, properly training networks on complicated tasks requires expertise and can be expensive from a computational perspective. In industrial applications, data coming from an open-world setting might widely differ from the benchmark datasets on which a network was trained. Being able to monitor the presence of such variations without retraining the network is of crucial importance. In this article, we develop a method to monitor trained neural networks based on the topological properties of their activation graphs. To each new observation, we assign a Topological Uncertainty, a score that aims to assess the reliability of the predictions by investigating the whole network instead of its final layer only, as typically done by practitioners. Our approach entirely works at a post-training level and does not require any assumption on the network architecture, optimization scheme, nor the use of data augmentation or auxiliary datasets; and can be faithfully applied on a large range of network architectures and data types. We showcase experimentally the potential of Topological Uncertainty in the context of trained network selection, Out-Of-Distribution detection, and shift-detection, both on synthetic and real datasets of images and graphs.

Quantitative stability of optimal transport maps and linearization of the 2-Wasserstein space

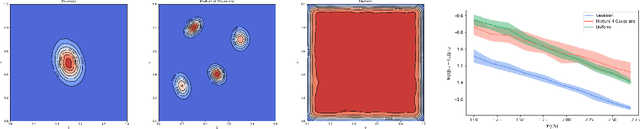
This work studies an explicit embedding of the set of probability measures into a Hilbert space, defined using optimal transport maps from a reference probability density. This embedding linearizes to some extent the 2-Wasserstein space, and enables the direct use of generic supervised and unsupervised learning algorithms on measure data. Our main result is that the embedding is (bi-)H\"older continuous, when the reference density is uniform over a convex set, and can be equivalently phrased as a dimension-independent H\"older-stability results for optimal transport maps.

ATOL: Automatic Topologically-Oriented Learning

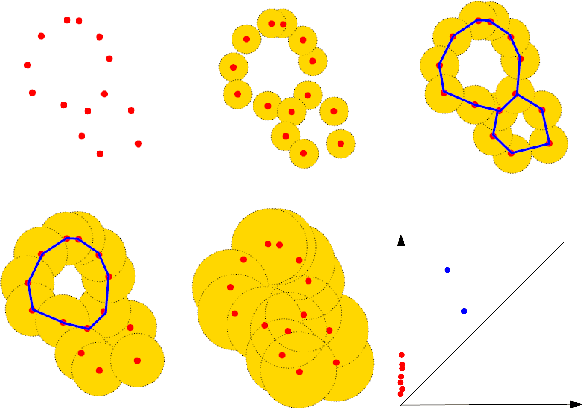
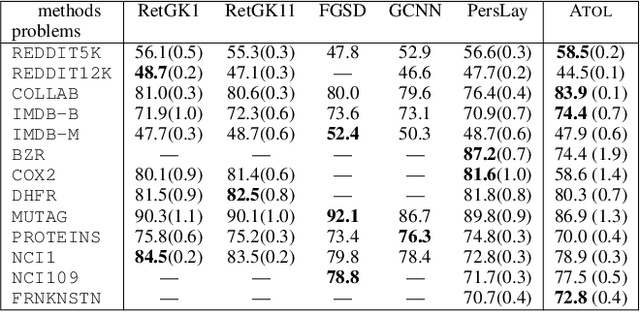
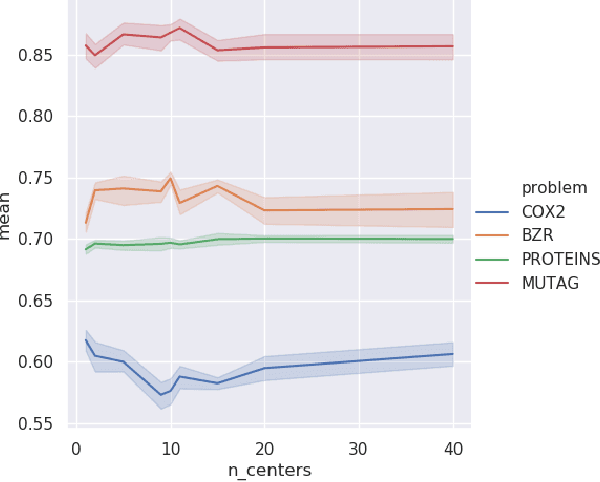
There are abundant cases for using Topological Data Analysis (TDA) in a learning context, but robust topological information commonly comes in the form of a set of persistence diagrams, objects that by nature are uneasy to affix to a generic machine learning framework. We introduce a vectorisation method for diagrams that allows to collect information from topological descriptors into a format fit for machine learning tools. Based on a few observations, the method is learned and tailored to discriminate the various important plane regions a diagram is set into. With this tool one can automatically augment any sort of machine learning problem with access to a TDA method, enhance performances, construct features reflecting underlying changes in topological behaviour. The proposed methodology comes with only high level tuning parameters such as the encoding budget for topological features. We provide an open-access, ready-to-use implementation and notebook. We showcase the strengths and versatility of our approach on a number of applications. From emulous and modern graph collections to a highly topological synthetic dynamical orbits data, we prove that the method matches or beats the state-of-the-art in encoding persistence diagrams to solve hard problems. We then apply our method in the context of an industrial, difficult time-series regression problem and show the approach to be relevant.

PersLay: A Simple and Versatile Neural Network Layer for Persistence Diagrams

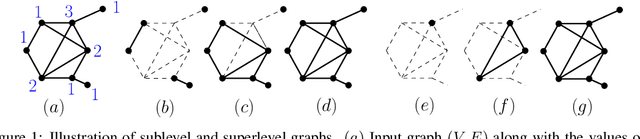
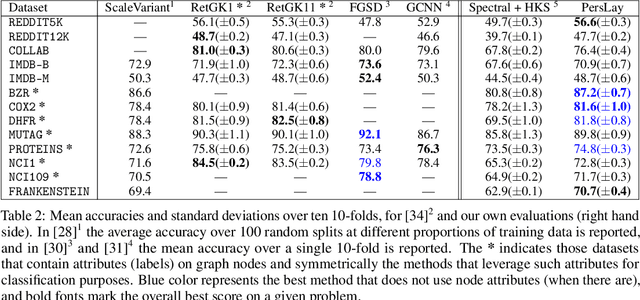
Persistence diagrams, a key descriptor from Topological Data Analysis, encode and summarize all sorts of topological features and have already proved pivotal in many different applications of data science. But persistence diagrams are weakly structured and therefore constitute a difficult input for most Machine Learning techniques. To address this concern several vectorization methods have been put forward that embed persistence diagrams into either finite-dimensional Euclidean spaces or implicit Hilbert spaces with kernels. But finite-dimensional embeddings are prone to miss a lot of information about persistence diagrams, while kernel methods require the full computation of the kernel matrix. We introduce PersLay: a simple, highly modular layer of learning architecture for persistence diagrams that allows to exploit the full capacities of neural networks on topological information from any dataset. This layer encompasses most of the vectorization methods of the literature. We illustrate its strengths on challenging classification problems on dynamical systems orbit or real-life graph data, with results improving or comparable to the state-of-the-art. In order to exploit topological information from graph data, we show how graph structures can be encoded in the so-called extended persistence diagrams computed with the heat kernel signatures of the graphs.

An introduction to Topological Data Analysis: fundamental and practical aspects for data scientists

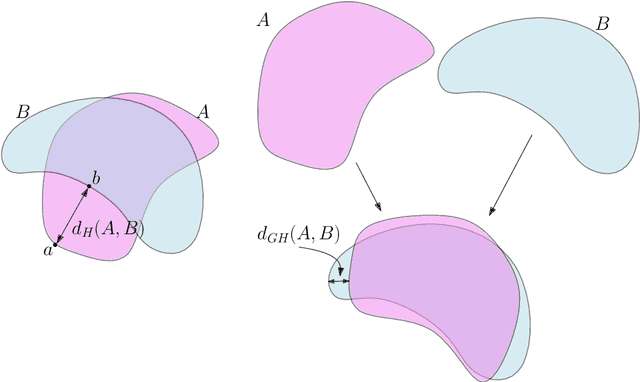
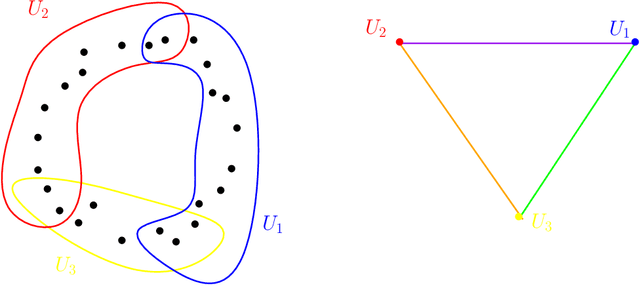
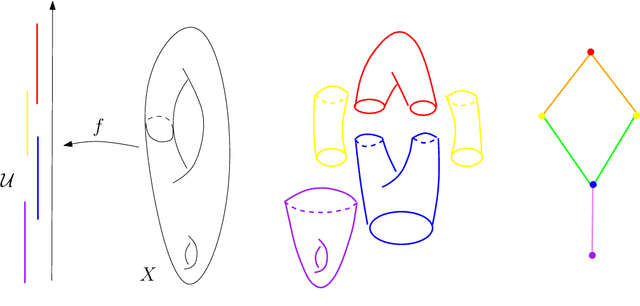
Topological Data Analysis (tda) is a recent and fast growing eld providing a set of new topological and geometric tools to infer relevant features for possibly complex data. This paper is a brief introduction, through a few selected topics, to basic fundamental and practical aspects of tda for non experts. 1 Introduction and motivation Topological Data Analysis (tda) is a recent eld that emerged from various works in applied (algebraic) topology and computational geometry during the rst decade of the century. Although one can trace back geometric approaches for data analysis quite far in the past, tda really started as a eld with the pioneering works of Edelsbrunner et al. (2002) and Zomorodian and Carlsson (2005) in persistent homology and was popularized in a landmark paper in 2009 Carlsson (2009). tda is mainly motivated by the idea that topology and geometry provide a powerful approach to infer robust qualitative, and sometimes quantitative, information about the structure of data-see, e.g. Chazal (2017). tda aims at providing well-founded mathematical, statistical and algorithmic methods to infer, analyze and exploit the complex topological and geometric structures underlying data that are often represented as point clouds in Euclidean or more general metric spaces. During the last few years, a considerable eort has been made to provide robust and ecient data structures and algorithms for tda that are now implemented and available and easy to use through standard libraries such as the Gudhi library (C++ and Python) Maria et al. (2014) and its R software interface Fasy et al. (2014a). Although it is still rapidly evolving, tda now provides a set of mature and ecient tools that can be used in combination or complementary to other data sciences tools. The tdapipeline. tda has recently known developments in various directions and application elds. There now exist a large variety of methods inspired by topological and geometric approaches. Providing a complete overview of all these existing approaches is beyond the scope of this introductory survey. However, most of them rely on the following basic and standard pipeline that will serve as the backbone of this paper: 1. The input is assumed to be a nite set of points coming with a notion of distance-or similarity between them. This distance can be induced by the metric in the ambient space (e.g. the Euclidean metric when the data are embedded in R d) or come as an intrinsic metric dened by a pairwise distance matrix. The denition of the metric on the data is usually given as an input or guided by the application. It is however important to notice that the choice of the metric may be critical to reveal interesting topological and geometric features of the data.