Transformers Learn Shortcuts to Automata

Algorithmic reasoning requires capabilities which are most naturally understood through recurrent models of computation, like the Turing machine. However, Transformer models, while lacking recurrence, are able to perform such reasoning using far fewer layers than the number of reasoning steps. This raises the question: what solutions are these shallow and non-recurrent models finding? We investigate this question in the setting of learning automata, discrete dynamical systems naturally suited to recurrent modeling and expressing algorithmic tasks. Our theoretical results completely characterize shortcut solutions, whereby a shallow Transformer with only $o(T)$ layers can exactly replicate the computation of an automaton on an input sequence of length $T$. By representing automata using the algebraic structure of their underlying transformation semigroups, we obtain $O(\log T)$-depth simulators for all automata and $O(1)$-depth simulators for all automata whose associated groups are solvable. Empirically, we perform synthetic experiments by training Transformers to simulate a wide variety of automata, and show that shortcut solutions can be learned via standard training. We further investigate the brittleness of these solutions and propose potential mitigations.

Recurrent Convolutional Neural Networks Learn Succinct Learning Algorithms

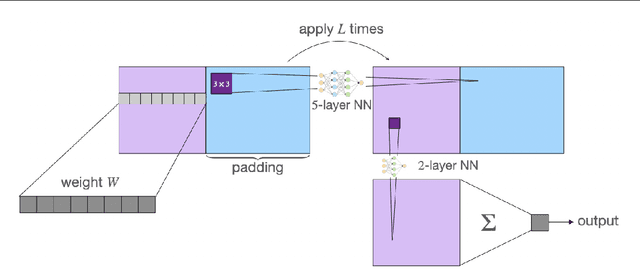
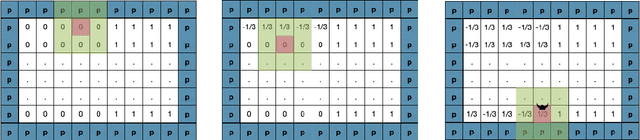
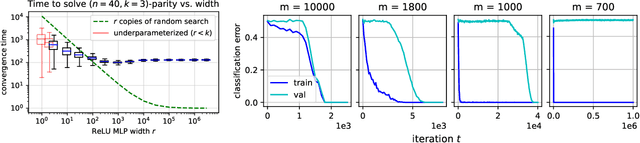
Neural Networks (NNs) struggle to efficiently learn certain problems, such as parity problems, even when there are simple learning algorithms for those problems. Can NNs discover learning algorithms on their own? We exhibit a NN architecture that, in polynomial time, learns as well as any efficient learning algorithm describable by a constant-sized learning algorithm. For example, on parity problems, the NN learns as well as row reduction, an efficient algorithm that can be succinctly described. Our architecture combines both recurrent weight-sharing between layers and convolutional weight-sharing to reduce the number of parameters down to a constant, even though the network itself may have trillions of nodes. While in practice the constants in our analysis are too large to be directly meaningful, our work suggests that the synergy of Recurrent and Convolutional NNs (RCNNs) may be more powerful than either alone.

Hidden Progress in Deep Learning: SGD Learns Parities Near the Computational Limit

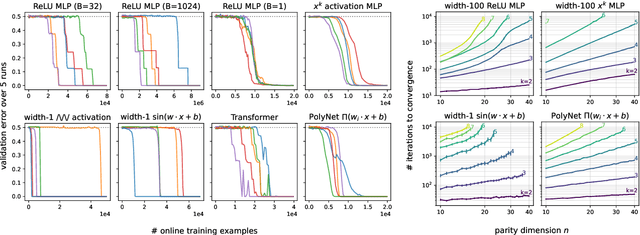
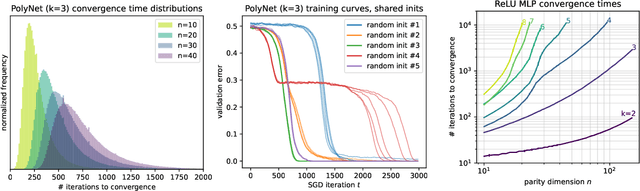
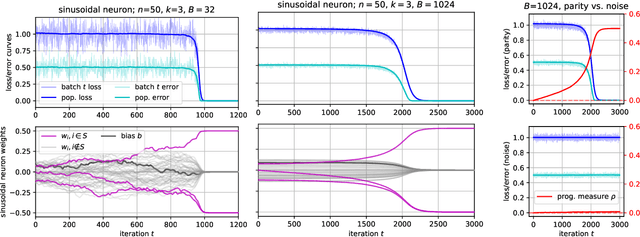
There is mounting empirical evidence of emergent phenomena in the capabilities of deep learning methods as we scale up datasets, model sizes, and training times. While there are some accounts of how these resources modulate statistical capacity, far less is known about their effect on the computational problem of model training. This work conducts such an exploration through the lens of learning $k$-sparse parities of $n$ bits, a canonical family of problems which pose theoretical computational barriers. In this setting, we find that neural networks exhibit surprising phase transitions when scaling up dataset size and running time. In particular, we demonstrate empirically that with standard training, a variety of architectures learn sparse parities with $n^{O(k)}$ examples, with loss (and error) curves abruptly dropping after $n^{O(k)}$ iterations. These positive results nearly match known SQ lower bounds, even without an explicit sparsity-promoting prior. We elucidate the mechanisms of these phenomena with a theoretical analysis: we find that the phase transition in performance is not due to SGD "stumbling in the dark" until it finds the hidden set of features (a natural algorithm which also runs in $n^{O(k)}$ time); instead, we show that SGD gradually amplifies a Fourier gap in the population gradient.

Understanding Contrastive Learning Requires Incorporating Inductive Biases

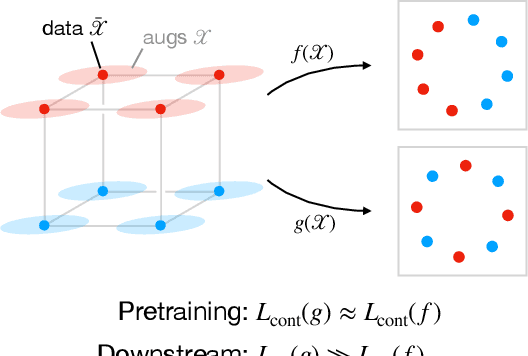
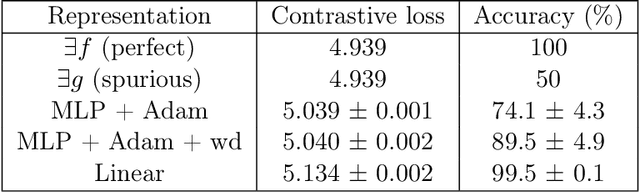
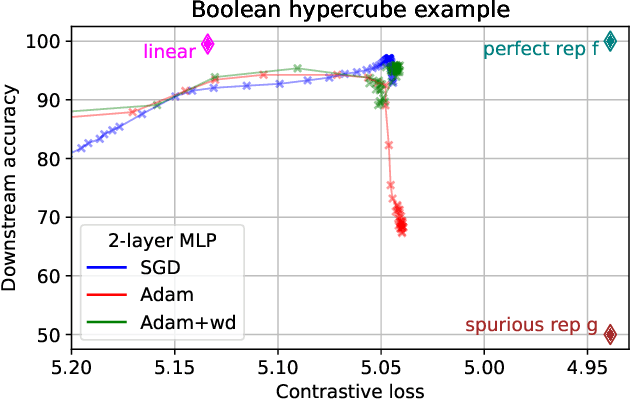
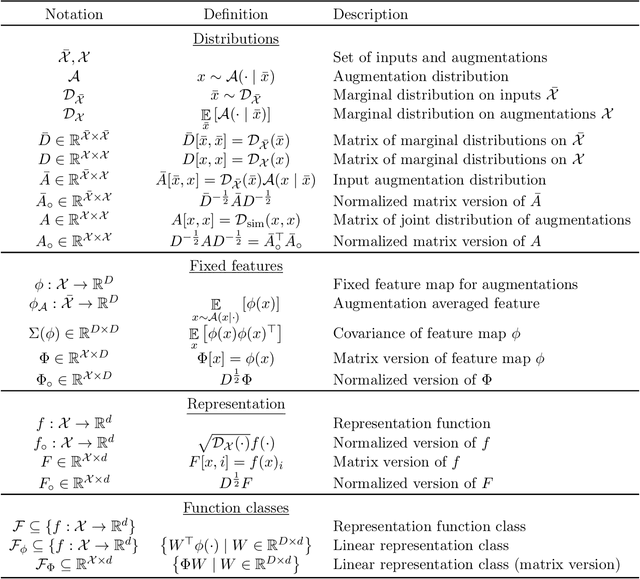
Contrastive learning is a popular form of self-supervised learning that encourages augmentations (views) of the same input to have more similar representations compared to augmentations of different inputs. Recent attempts to theoretically explain the success of contrastive learning on downstream classification tasks prove guarantees depending on properties of {\em augmentations} and the value of {\em contrastive loss} of representations. We demonstrate that such analyses, that ignore {\em inductive biases} of the function class and training algorithm, cannot adequately explain the success of contrastive learning, even {\em provably} leading to vacuous guarantees in some settings. Extensive experiments on image and text domains highlight the ubiquity of this problem -- different function classes and algorithms behave very differently on downstream tasks, despite having the same augmentations and contrastive losses. Theoretical analysis is presented for the class of linear representations, where incorporating inductive biases of the function class allows contrastive learning to work with less stringent conditions compared to prior analyses.

Anti-Concentrated Confidence Bonuses for Scalable Exploration

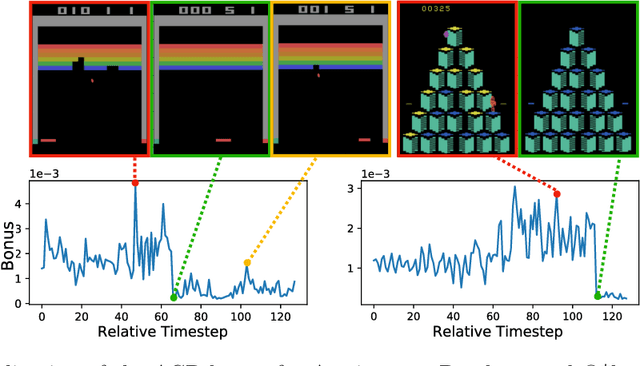
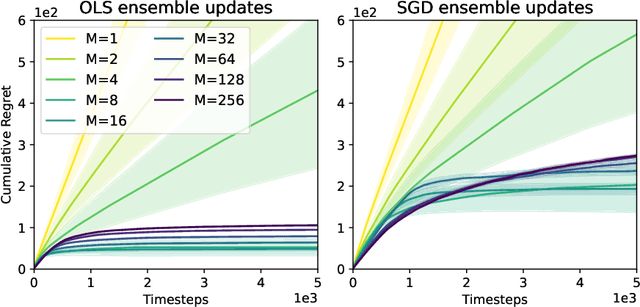
Intrinsic rewards play a central role in handling the exploration-exploitation trade-off when designing sequential decision-making algorithms, in both foundational theory and state-of-the-art deep reinforcement learning. The LinUCB algorithm, a centerpiece of the stochastic linear bandits literature, prescribes an elliptical bonus which addresses the challenge of leveraging shared information in large action spaces. This bonus scheme cannot be directly transferred to high-dimensional exploration problems, however, due to the computational cost of maintaining the inverse covariance matrix of action features. We introduce \emph{anti-concentrated confidence bounds} for efficiently approximating the elliptical bonus, using an ensemble of regressors trained to predict random noise from policy network-derived features. Using this approximation, we obtain stochastic linear bandit algorithms which obtain $\tilde O(d \sqrt{T})$ regret bounds for $\mathrm{poly}(d)$ fixed actions. We develop a practical variant for deep reinforcement learning that is competitive with contemporary intrinsic reward heuristics on Atari benchmarks.

Inductive Biases and Variable Creation in Self-Attention Mechanisms

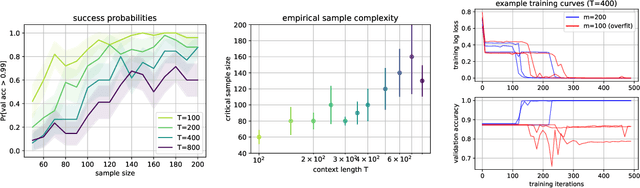
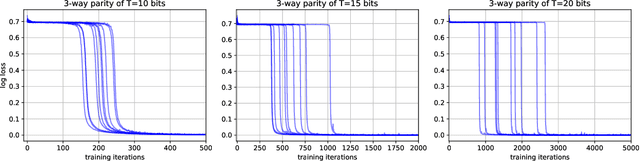
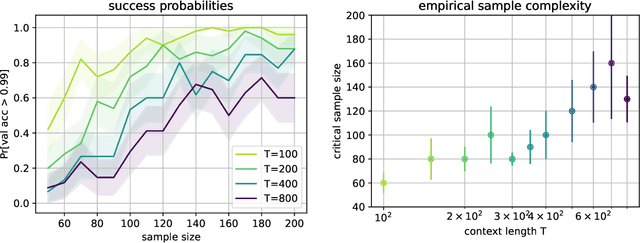
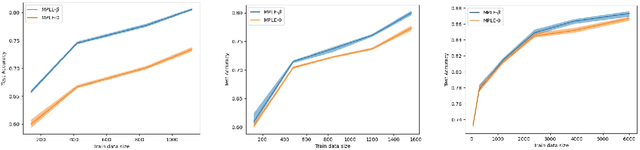
Self-attention, an architectural motif designed to model long-range interactions in sequential data, has driven numerous recent breakthroughs in natural language processing and beyond. This work provides a theoretical analysis of the inductive biases of self-attention modules, where our focus is to rigorously establish which functions and long-range dependencies self-attention blocks prefer to represent. Our main result shows that bounded-norm Transformer layers create sparse variables: they can represent sparse functions of the input sequence, with sample complexity scaling only logarithmically with the context length. Furthermore, we propose new experimental protocols to support this analysis and to guide the practice of training Transformers, built around the large body of work on provably learning sparse Boolean functions.

Statistical Estimation from Dependent Data

We consider a general statistical estimation problem wherein binary labels across different observations are not independent conditioned on their feature vectors, but dependent, capturing settings where e.g. these observations are collected on a spatial domain, a temporal domain, or a social network, which induce dependencies. We model these dependencies in the language of Markov Random Fields and, importantly, allow these dependencies to be substantial, i.e do not assume that the Markov Random Field capturing these dependencies is in high temperature. As our main contribution we provide algorithms and statistically efficient estimation rates for this model, giving several instantiations of our bounds in logistic regression, sparse logistic regression, and neural network settings with dependent data. Our estimation guarantees follow from novel results for estimating the parameters (i.e. external fields and interaction strengths) of Ising models from a {\em single} sample. {We evaluate our estimation approach on real networked data, showing that it outperforms standard regression approaches that ignore dependencies, across three text classification datasets: Cora, Citeseer and Pubmed.}

Investigating the Role of Negatives in Contrastive Representation Learning

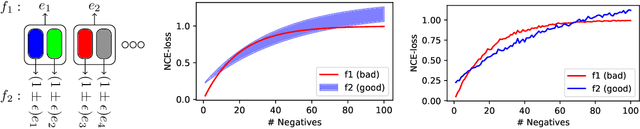
Noise contrastive learning is a popular technique for unsupervised representation learning. In this approach, a representation is obtained via reduction to supervised learning, where given a notion of semantic similarity, the learner tries to distinguish a similar (positive) example from a collection of random (negative) examples. The success of modern contrastive learning pipelines relies on many parameters such as the choice of data augmentation, the number of negative examples, and the batch size; however, there is limited understanding as to how these parameters interact and affect downstream performance. We focus on disambiguating the role of one of these parameters: the number of negative examples. Theoretically, we show the existence of a collision-coverage trade-off suggesting that the optimal number of negative examples should scale with the number of underlying concepts in the data. Empirically, we scrutinize the role of the number of negatives in both NLP and vision tasks. In the NLP task, we find that the results broadly agree with our theory, while our vision experiments are murkier with performance sometimes even being insensitive to the number of negatives. We discuss plausible explanations for this behavior and suggest future directions to better align theory and practice.

Gone Fishing: Neural Active Learning with Fisher Embeddings

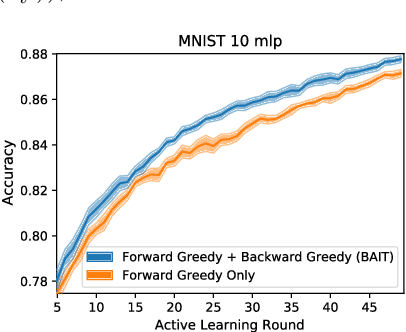
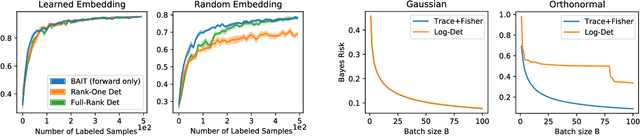
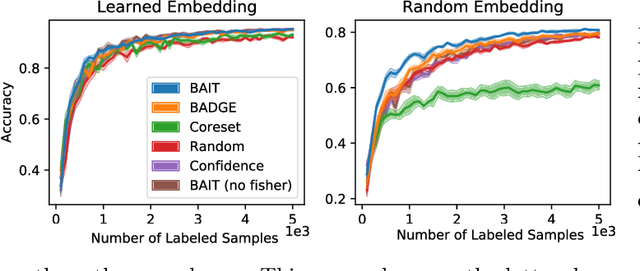
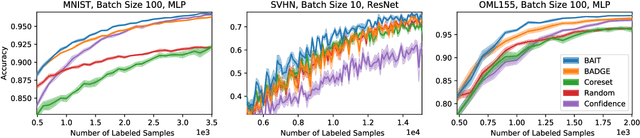
There is an increasing need for effective active learning algorithms that are compatible with deep neural networks. While there are many classic, well-studied sample selection methods, the non-convexity and varying internal representation of neural models make it unclear how to extend these approaches. This article introduces BAIT, a practical, tractable, and high-performing active learning algorithm for neural networks that addresses these concerns. BAIT draws inspiration from the theoretical analysis of maximum likelihood estimators (MLE) for parametric models. It selects batches of samples by optimizing a bound on the MLE error in terms of the Fisher information, which we show can be implemented efficiently at scale by exploiting linear-algebraic structure especially amenable to execution on modern hardware. Our experiments show that BAIT outperforms the previous state of the art on both classification and regression problems, and is flexible enough to be used with a variety of model architectures.

Acceleration via Fractal Learning Rate Schedules

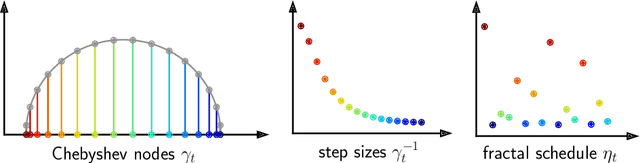
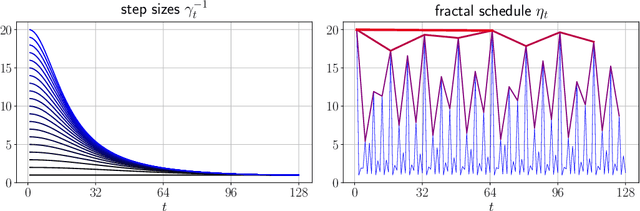
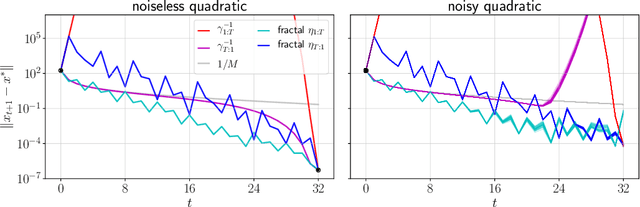
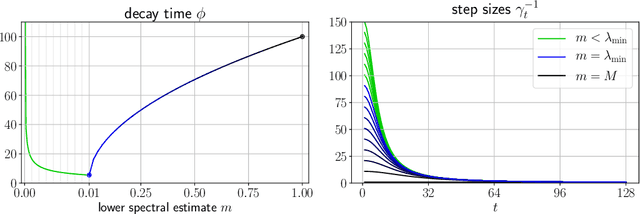
When balancing the practical tradeoffs of iterative methods for large-scale optimization, the learning rate schedule remains notoriously difficult to understand and expensive to tune. We demonstrate the presence of these subtleties even in the innocuous case when the objective is a convex quadratic. We reinterpret an iterative algorithm from the numerical analysis literature as what we call the Chebyshev learning rate schedule for accelerating vanilla gradient descent, and show that the problem of mitigating instability leads to a fractal ordering of step sizes. We provide some experiments and discussion to challenge current understandings of the "edge of stability" in deep learning: even in simple settings, provable acceleration can be obtained by making negative local progress on the objective.