Depth Separations in Neural Networks: Separating the Dimension from the Accuracy

We prove an exponential separation between depth 2 and depth 3 neural networks, when approximating an $\mathcal{O}(1)$-Lipschitz target function to constant accuracy, with respect to a distribution with support in $[0,1]^{d}$, assuming exponentially bounded weights. This addresses an open problem posed in \citet{safran2019depth}, and proves that the curse of dimensionality manifests in depth 2 approximation, even in cases where the target function can be represented efficiently using depth 3. Previously, lower bounds that were used to separate depth 2 from depth 3 required that at least one of the Lipschitz parameter, target accuracy or (some measure of) the size of the domain of approximation scale polynomially with the input dimension, whereas we fix the former two and restrict our domain to the unit hypercube. Our lower bound holds for a wide variety of activation functions, and is based on a novel application of an average- to worst-case random self-reducibility argument, to reduce the problem to threshold circuits lower bounds.

How Many Neurons Does it Take to Approximate the Maximum?

We study the size of a neural network needed to approximate the maximum function over $d$ inputs, in the most basic setting of approximating with respect to the $L_2$ norm, for continuous distributions, for a network that uses ReLU activations. We provide new lower and upper bounds on the width required for approximation across various depths. Our results establish new depth separations between depth 2 and 3, and depth 3 and 5 networks, as well as providing a depth $\mathcal{O}(\log(\log(d)))$ and width $\mathcal{O}(d)$ construction which approximates the maximum function, significantly improving upon the depth requirements of the best previously known bounds for networks with linearly-bounded width. Our depth separation results are facilitated by a new lower bound for depth 2 networks approximating the maximum function over the uniform distribution, assuming an exponential upper bound on the size of the weights. Furthermore, we are able to use this depth 2 lower bound to provide tight bounds on the number of neurons needed to approximate the maximum by a depth 3 network. Our lower bounds are of potentially broad interest as they apply to the widely studied and used \emph{max} function, in contrast to many previous results that base their bounds on specially constructed or pathological functions and distributions.

Size and depth of monotone neural networks: interpolation and approximation

Monotone functions and data sets arise in a variety of applications. We study the interpolation problem for monotone data sets: The input is a monotone data set with $n$ points, and the goal is to find a size and depth efficient monotone neural network, with non negative parameters and threshold units, that interpolates the data set. We show that there are monotone data sets that cannot be interpolated by a monotone network of depth $2$. On the other hand, we prove that for every monotone data set with $n$ points in $\mathbb{R}^d$, there exists an interpolating monotone network of depth $4$ and size $O(nd)$. Our interpolation result implies that every monotone function over $[0,1]^d$ can be approximated arbitrarily well by a depth-4 monotone network, improving the previous best-known construction of depth $d+1$. Finally, building on results from Boolean circuit complexity, we show that the inductive bias of having positive parameters can lead to a super-polynomial blow-up in the number of neurons when approximating monotone functions.

Size and Depth Separation in Approximating Natural Functions with Neural Networks

When studying the expressive power of neural networks, a main challenge is to understand how the size and depth of the network affect its ability to approximate real functions. However, not all functions are interesting from a practical viewpoint: functions of interest usually have a polynomially-bounded Lipschitz constant, and can be computed efficiently. We call functions that satisfy these conditions "natural", and explore the benefits of size and depth for approximation of natural functions with ReLU networks. As we show, this problem is more challenging than the corresponding problem for non-natural functions. We give barriers to showing depth-lower-bounds: Proving existence of a natural function that cannot be approximated by polynomial-size networks of depth $4$ would settle longstanding open problems in computational complexity. It implies that beyond depth $4$ there is a barrier to showing depth-separation for natural functions, even between networks of constant depth and networks of nonconstant depth. We also study size-separation, namely, whether there are natural functions that can be approximated with networks of size $O(s(d))$, but not with networks of size $O(s'(d))$. We show a complexity-theoretic barrier to proving such results beyond size $O(d\log^2(d))$, but also show an explicit natural function, that can be approximated with networks of size $O(d)$ and not with networks of size $o(d/\log d)$. For approximation in $L_\infty$ we achieve such separation already between size $O(d)$ and size $o(d)$. Moreover, we show superpolynomial size lower bounds and barriers to such lower bounds, depending on the assumptions on the function. Our size-separation results rely on an analysis of size lower bounds for Boolean functions, which is of independent interest: We show linear size lower bounds for computing explicit Boolean functions with neural networks and threshold circuits.

Tight Hardness Results for Training Depth-2 ReLU Networks

We prove several hardness results for training depth-2 neural networks with the ReLU activation function; these networks are simply weighted sums (that may include negative coefficients) of ReLUs. Our goal is to output a depth-2 neural network that minimizes the square loss with respect to a given training set. We prove that this problem is NP-hard already for a network with a single ReLU. We also prove NP-hardness for outputting a weighted sum of $k$ ReLUs minimizing the squared error (for $k>1$) even in the realizable setting (i.e., when the labels are consistent with an unknown depth-2 ReLU network). We are also able to obtain lower bounds on the running time in terms of the desired additive error $\epsilon$. To obtain our lower bounds, we use the Gap Exponential Time Hypothesis (Gap-ETH) as well as a new hypothesis regarding the hardness of approximating the well known Densest $\kappa$-Subgraph problem in subexponential time (these hypotheses are used separately in proving different lower bounds). For example, we prove that under reasonable hardness assumptions, any proper learning algorithm for finding the best fitting ReLU must run in time exponential in $1/\epsilon^2$. Together with a previous work regarding improperly learning a ReLU (Goel et al., COLT'17), this implies the first separation between proper and improper algorithms for learning a ReLU. We also study the problem of properly learning a depth-2 network of ReLUs with bounded weights giving new (worst-case) upper bounds on the running time needed to learn such networks both in the realizable and agnostic settings. Our upper bounds on the running time essentially matches our lower bounds in terms of the dependency on $\epsilon$.

Cognitive Model Priors for Predicting Human Decisions

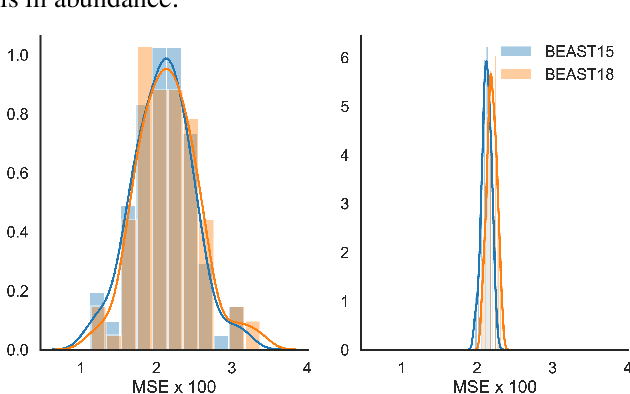
Human decision-making underlies all economic behavior. For the past four decades, human decision-making under uncertainty has continued to be explained by theoretical models based on prospect theory, a framework that was awarded the Nobel Prize in Economic Sciences. However, theoretical models of this kind have developed slowly, and robust, high-precision predictive models of human decisions remain a challenge. While machine learning is a natural candidate for solving these problems, it is currently unclear to what extent it can improve predictions obtained by current theories. We argue that this is mainly due to data scarcity, since noisy human behavior requires massive sample sizes to be accurately captured by off-the-shelf machine learning methods. To solve this problem, what is needed are machine learning models with appropriate inductive biases for capturing human behavior, and larger datasets. We offer two contributions towards this end: first, we construct "cognitive model priors" by pretraining neural networks with synthetic data generated by cognitive models (i.e., theoretical models developed by cognitive psychologists). We find that fine-tuning these networks on small datasets of real human decisions results in unprecedented state-of-the-art improvements on two benchmark datasets. Second, we present the first large-scale dataset for human decision-making, containing over 240,000 human judgments across over 13,000 decision problems. This dataset reveals the circumstances where cognitive model priors are useful, and provides a new standard for benchmarking prediction of human decisions under uncertainty.

Predicting human decisions with behavioral theories and machine learning

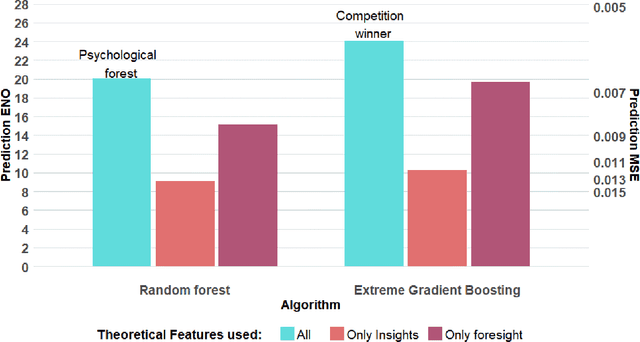
Behavioral decision theories aim to explain human behavior. Can they help predict it? An open tournament for prediction of human choices in fundamental economic decision tasks is presented. The results suggest that integration of certain behavioral theories as features in machine learning systems provides the best predictions. Surprisingly, the most useful theories for prediction build on basic properties of human and animal learning and are very different from mainstream decision theories that focus on deviations from rational choice. Moreover, we find that theoretical features should be based not only on qualitative behavioral insights (e.g. loss aversion), but also on quantitative behavioral foresights generated by functional descriptive models (e.g. Prospect Theory). Our analysis prescribes a recipe for derivation of explainable, useful predictions of human decisions.

gprHOG and the popularity of Histogram of Oriented Gradients for Buried Threat Detection in Ground-Penetrating Radar

Substantial research has been devoted to the development of algorithms that automate buried threat detection (BTD) with ground penetrating radar (GPR) data, resulting in a large number of proposed algorithms. One popular algorithm GPR-based BTD, originally applied by Torrione et al., 2012, is the Histogram of Oriented Gradients (HOG) feature. In a recent large-scale comparison among five veteran institutions, a modified version of HOG referred to here as "gprHOG", performed poorly compared to other modern algorithms. In this paper, we provide experimental evidence demonstrating that the modifications to HOG that comprise gprHOG result in a substantially better-performing algorithm. The results here, in conjunction with the large-scale algorithm comparison, suggest that HOG is not competitive with modern GPR-based BTD algorithms. Given HOG's popularity, these results raise some questions about many existing studies, and suggest gprHOG (and especially HOG) should be employed with caution in future studies.

A Large-Scale Multi-Institutional Evaluation of Advanced Discrimination Algorithms for Buried Threat Detection in Ground Penetrating Radar

In this paper we consider the development of algorithms for the automatic detection of buried threats using ground penetrating radar (GPR) measurements. GPR is one of the most studied and successful modalities for automatic buried threat detection (BTD), and a large variety of BTD algorithms have been proposed for it. Despite this, large-scale comparisons of GPR-based BTD algorithms are rare in the literature. In this work we report the results of a multi-institutional effort to develop advanced buried threat detection algorithms for a real-world GPR BTD system. The effort involved five institutions with substantial experience with the development of GPR-based BTD algorithms. In this paper we report the technical details of the advanced algorithms submitted by each institution, representing their latest technical advances, and many state-of-the-art GPR-based BTD algorithms. We also report the results of evaluating the algorithms from each institution on the large experimental dataset used for development. The experimental dataset comprised 120,000 m^2 of GPR data using surface area, from 13 different lanes across two US test sites. The data was collected using a vehicle-mounted GPR system, the variants of which have supplied data for numerous publications. Using these results, we identify the most successful and common processing strategies among the submitted algorithms, and make recommendations for GPR-based BTD algorithm design.

Dense labeling of large remote sensing imagery with convolutional neural networks: a simple and faster alternative to stitching output label maps

In this work we consider the application of convolutional neural networks (CNNs) for pixel-wise labeling (a.k.a., semantic segmentation) of remote sensing imagery (e.g., aerial color or hyperspectral imagery). Remote sensing imagery is usually stored in the form of very large images, referred to as "tiles", which are too large to be segmented directly using most CNNs and their associated hardware. As a result, during label inference, smaller sub-images, called "patches", are processed individually and then "stitched" (concatenated) back together to create a tile-sized label map. This approach suffers from computational ineffiency and can result in discontinuities at output boundaries. We propose a simple alternative approach in which the input size of the CNN is dramatically increased only during label inference. This does not avoid stitching altogether, but substantially mitigates its limitations. We evaluate the performance of the proposed approach against a vonventional stitching approach using two popular segmentation CNN models and two large-scale remote sensing imagery datasets. The results suggest that the proposed approach substantially reduces label inference time, while also yielding modest overall label accuracy increases. This approach contributed to our wining entry (overall performance) in the INRIA building labeling competition.