Learning Hard-Constrained Models with One Sample

We consider the problem of estimating the parameters of a Markov Random Field with hard-constraints using a single sample. As our main running examples, we use the $k$-SAT and the proper coloring models, as well as general $H$-coloring models; for all of these we obtain both positive and negative results. In contrast to the soft-constrained case, we show in particular that single-sample estimation is not always possible, and that the existence of an estimator is related to the existence of non-satisfiable instances. Our algorithms are based on the pseudo-likelihood estimator. We show variance bounds for this estimator using coupling techniques inspired, in the case of $k$-SAT, by Moitra's sampling algorithm (JACM, 2019); our positive results for colorings build on this new coupling approach. For $q$-colorings on graphs with maximum degree $d$, we give a linear-time estimator when $q>d+1$, whereas the problem is non-identifiable when $q\leq d+1$. For general $H$-colorings, we show that standard conditions that guarantee sampling, such as Dobrushin's condition, are insufficient for one-sample learning; on the positive side, we provide a general condition that is sufficient to guarantee linear-time learning and obtain applications for proper colorings and permissive models. For the $k$-SAT model on formulas with maximum degree $d$, we provide a linear-time estimator when $k\gtrsim 6.45\log d$, whereas the problem becomes non-identifiable when $k\lesssim \log d$.

EM's Convergence in Gaussian Latent Tree Models

We study the optimization landscape of the log-likelihood function and the convergence of the Expectation-Maximization (EM) algorithm in latent Gaussian tree models, i.e. tree-structured Gaussian graphical models whose leaf nodes are observable and non-leaf nodes are unobservable. We show that the unique non-trivial stationary point of the population log-likelihood is its global maximum, and establish that the expectation-maximization algorithm is guaranteed to converge to it in the single latent variable case. Our results for the landscape of the log-likelihood function in general latent tree models provide support for the extensive practical use of maximum likelihood based-methods in this setting. Our results for the EM algorithm extend an emerging line of work on obtaining global convergence guarantees for this celebrated algorithm. We show our results for the non-trivial stationary points of the log-likelihood by arguing that a certain system of polynomial equations obtained from the EM updates has a unique non-trivial solution. The global convergence of the EM algorithm follows by arguing that all trivial fixed points are higher-order saddle points.

Learning and Testing Latent-Tree Ising Models Efficiently

We provide time- and sample-efficient algorithms for learning and testing latent-tree Ising models, i.e. Ising models that may only be observed at their leaf nodes. On the learning side, we obtain efficient algorithms for learning a tree-structured Ising model whose leaf node distribution is close in Total Variation Distance, improving on the results of prior work. On the testing side, we provide an efficient algorithm with fewer samples for testing whether two latent-tree Ising models have leaf-node distributions that are close or far in Total Variation distance. We obtain our algorithms by showing novel localization results for the total variation distance between the leaf-node distributions of tree-structured Ising models, in terms of their marginals on pairs of leaves.

Statistical Estimation from Dependent Data

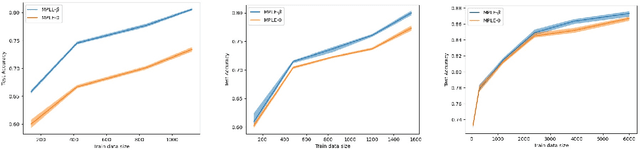
We consider a general statistical estimation problem wherein binary labels across different observations are not independent conditioned on their feature vectors, but dependent, capturing settings where e.g. these observations are collected on a spatial domain, a temporal domain, or a social network, which induce dependencies. We model these dependencies in the language of Markov Random Fields and, importantly, allow these dependencies to be substantial, i.e do not assume that the Markov Random Field capturing these dependencies is in high temperature. As our main contribution we provide algorithms and statistically efficient estimation rates for this model, giving several instantiations of our bounds in logistic regression, sparse logistic regression, and neural network settings with dependent data. Our estimation guarantees follow from novel results for estimating the parameters (i.e. external fields and interaction strengths) of Ising models from a {\em single} sample. {We evaluate our estimation approach on real networked data, showing that it outperforms standard regression approaches that ignore dependencies, across three text classification datasets: Cora, Citeseer and Pubmed.}

Estimating Ising Models from One Sample

Given one sample $X \in \{\pm 1\}^n$ from an Ising model $\Pr[X=x]\propto \exp(x^\top J x/2)$, whose interaction matrix satisfies $J:= \sum_{i=1}^k \beta_i J_i$ for some known matrices $J_i$ and some unknown parameters $\beta_i$, we study whether $J$ can be estimated to high accuracy. Assuming that each node of the Ising model has bounded total interaction with the other nodes, i.e. $\|J\|_{\infty} \le O(1)$, we provide a computationally efficient estimator $\hat{J}$ with the high probability guarantee $\|\hat{J} -J\|_F \le \widetilde O(\sqrt{k})$, where $\|J\|_F$ can be as high as $\Omega(\sqrt{n})$. Our guarantee is tight when the interaction strengths are sufficiently low. An example application of our result is in social networks, wherein nodes make binary choices, $x_1,\ldots,x_n$, which may be influenced at varying strengths $\beta_i$ by different networks $J_i$ in which these nodes belong. By observing a single snapshot of the nodes' behaviors the goal is to learn the combined correlation structure. When $k=1$ and a single parameter is to be inferred, we further show $|\hat{\beta}_1 - \beta_1| \le \widetilde O(F(\beta_1J_1)^{-1/2})$, where $F(\beta_1J_1)$ is the log-partition function of the model. This was proved in prior work under additional assumptions. We generalize these results to any setting. While our guarantees aim both high and low temperature regimes, our proof relies on sparsifying the correlation network by conditioning on subsets of the variables, such that the unconditioned variables satisfy Dobrushin's condition, i.e. a high temperature condition which allows us to apply stronger concentration inequalities. We use this to prove concentration and anti-concentration properties of the Ising model, and we believe this sparsification result has applications beyond the scope of this paper as well.