Online Learning in Periodic Zero-Sum Games

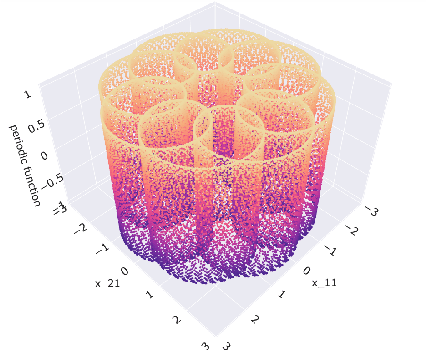
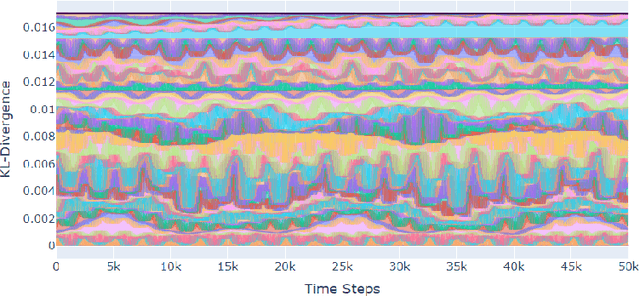
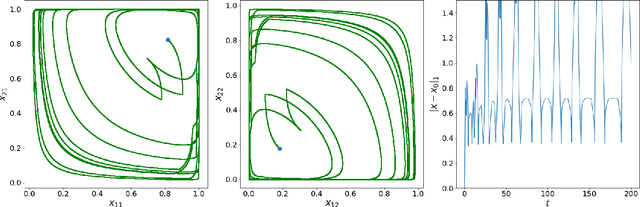
A seminal result in game theory is von Neumann's minmax theorem, which states that zero-sum games admit an essentially unique equilibrium solution. Classical learning results build on this theorem to show that online no-regret dynamics converge to an equilibrium in a time-average sense in zero-sum games. In the past several years, a key research direction has focused on characterizing the day-to-day behavior of such dynamics. General results in this direction show that broad classes of online learning dynamics are cyclic, and formally Poincar\'{e} recurrent, in zero-sum games. We analyze the robustness of these online learning behaviors in the case of periodic zero-sum games with a time-invariant equilibrium. This model generalizes the usual repeated game formulation while also being a realistic and natural model of a repeated competition between players that depends on exogenous environmental variations such as time-of-day effects, week-to-week trends, and seasonality. Interestingly, time-average convergence may fail even in the simplest such settings, in spite of the equilibrium being fixed. In contrast, using novel analysis methods, we show that Poincar\'{e} recurrence provably generalizes despite the complex, non-autonomous nature of these dynamical systems.

Efficient Online Learning for Dynamic k-Clustering

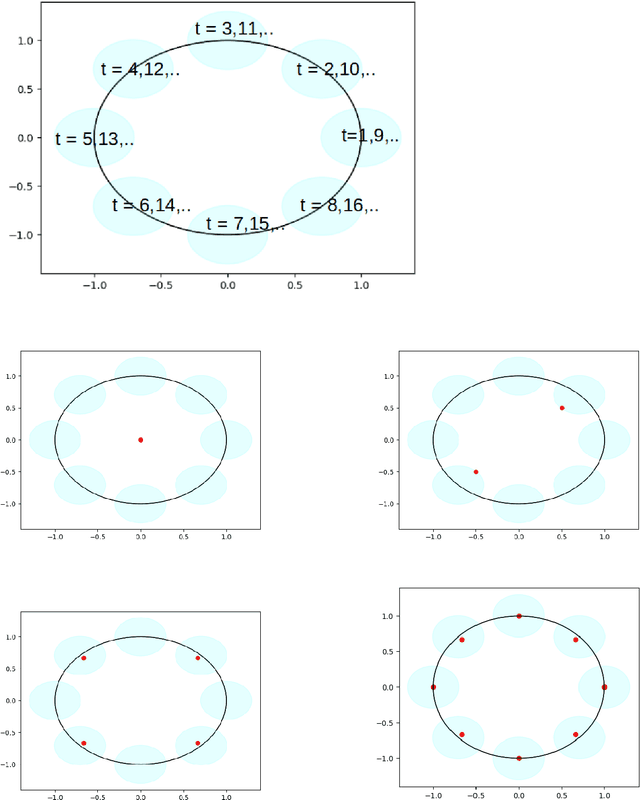
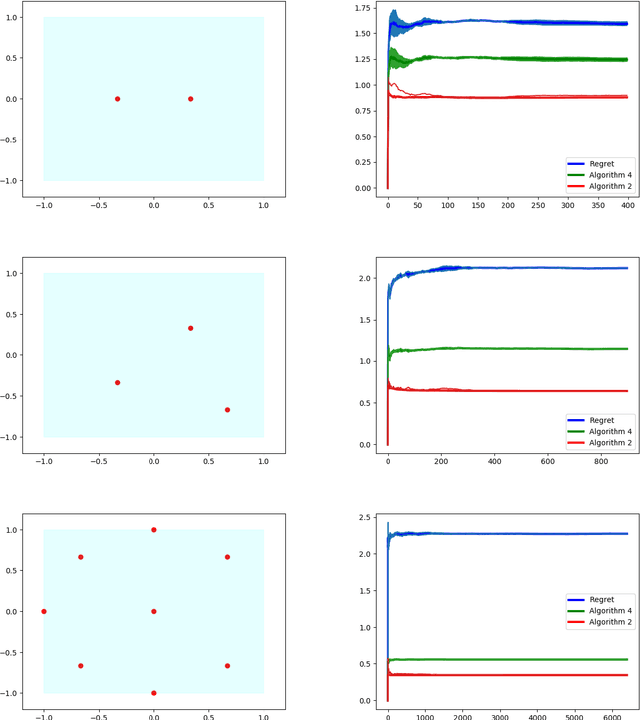
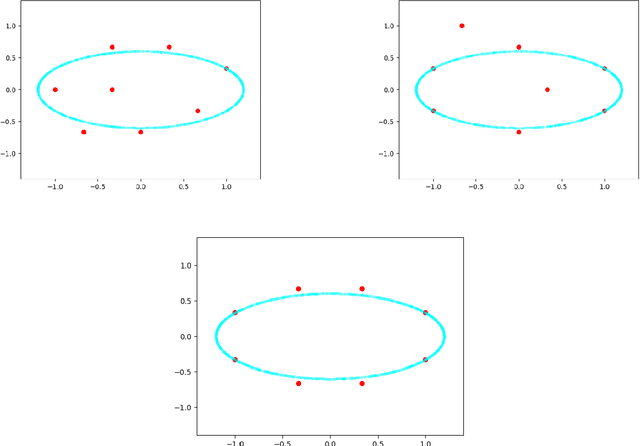
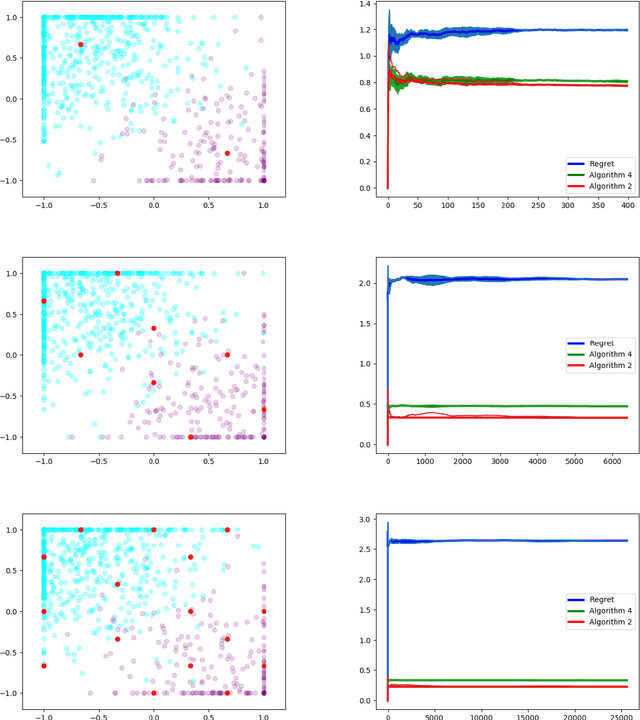
We study dynamic clustering problems from the perspective of online learning. We consider an online learning problem, called \textit{Dynamic $k$-Clustering}, in which $k$ centers are maintained in a metric space over time (centers may change positions) such as a dynamically changing set of $r$ clients is served in the best possible way. The connection cost at round $t$ is given by the \textit{$p$-norm} of the vector consisting of the distance of each client to its closest center at round $t$, for some $p\geq 1$ or $p = \infty$. We present a \textit{$\Theta\left( \min(k,r) \right)$-regret} polynomial-time online learning algorithm and show that, under some well-established computational complexity conjectures, \textit{constant-regret} cannot be achieved in polynomial-time. In addition to the efficient solution of Dynamic $k$-Clustering, our work contributes to the long line of research on combinatorial online learning.

Evolutionary Game Theory Squared: Evolving Agents in Endogenously Evolving Zero-Sum Games

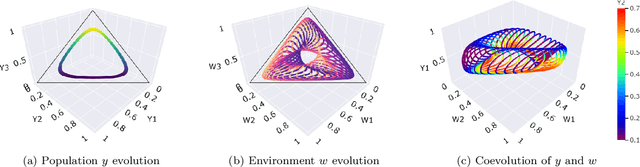
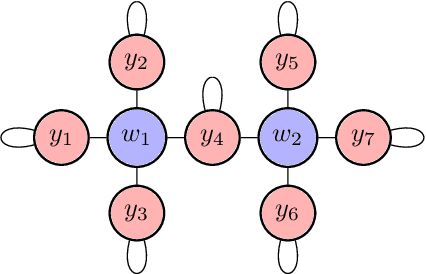
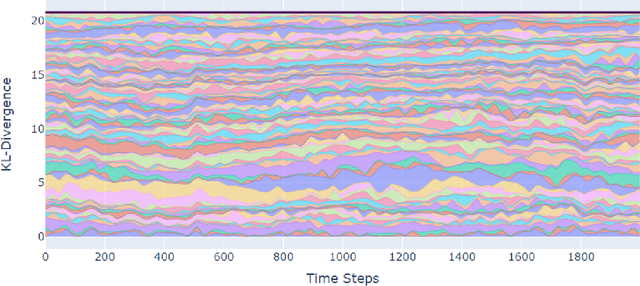
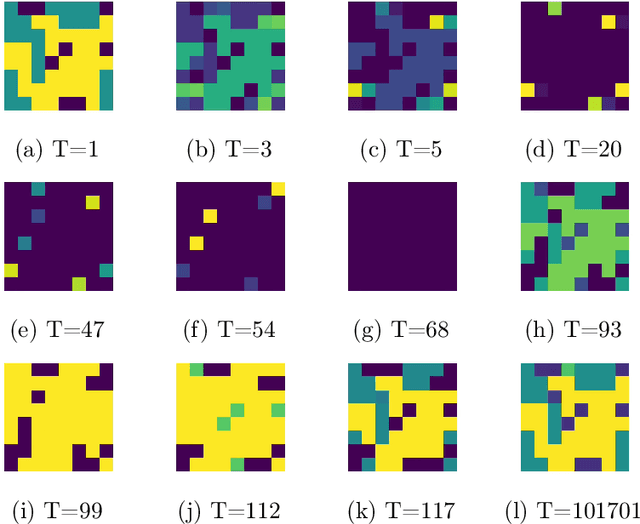
The predominant paradigm in evolutionary game theory and more generally online learning in games is based on a clear distinction between a population of dynamic agents that interact given a fixed, static game. In this paper, we move away from the artificial divide between dynamic agents and static games, to introduce and analyze a large class of competitive settings where both the agents and the games they play evolve strategically over time. We focus on arguably the most archetypal game-theoretic setting -- zero-sum games (as well as network generalizations) -- and the most studied evolutionary learning dynamic -- replicator, the continuous-time analogue of multiplicative weights. Populations of agents compete against each other in a zero-sum competition that itself evolves adversarially to the current population mixture. Remarkably, despite the chaotic coevolution of agents and games, we prove that the system exhibits a number of regularities. First, the system has conservation laws of an information-theoretic flavor that couple the behavior of all agents and games. Secondly, the system is Poincar\'{e} recurrent, with effectively all possible initializations of agents and games lying on recurrent orbits that come arbitrarily close to their initial conditions infinitely often. Thirdly, the time-average agent behavior and utility converge to the Nash equilibrium values of the time-average game. Finally, we provide a polynomial time algorithm to efficiently predict this time-average behavior for any such coevolving network game.

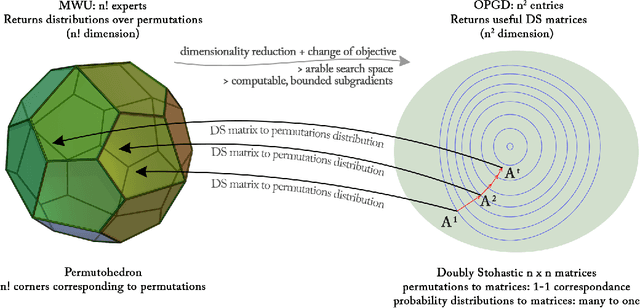
Efficient Online Learning of Optimal Rankings: Dimensionality Reduction via Gradient Descent

We consider a natural model of online preference aggregation, where sets of preferred items $R_1, R_2, \ldots, R_t$ along with a demand for $k_t$ items in each $R_t$, appear online. Without prior knowledge of $(R_t, k_t)$, the learner maintains a ranking $\pi_t$ aiming that at least $k_t$ items from $R_t$ appear high in $\pi_t$. This is a fundamental problem in preference aggregation with applications to, e.g., ordering product or news items in web pages based on user scrolling and click patterns. The widely studied Generalized Min-Sum-Set-Cover (GMSSC) problem serves as a formal model for the setting above. GMSSC is NP-hard and the standard application of no-regret online learning algorithms is computationally inefficient, because they operate in the space of rankings. In this work, we show how to achieve low regret for GMSSC in polynomial-time. We employ dimensionality reduction from rankings to the space of doubly stochastic matrices, where we apply Online Gradient Descent. A key step is to show how subgradients can be computed efficiently, by solving the dual of a configuration LP. Using oblivious deterministic and randomized rounding schemes, we map doubly stochastic matrices back to rankings with a small loss in the GMSSC objective.

The Complexity of Constrained Min-Max Optimization

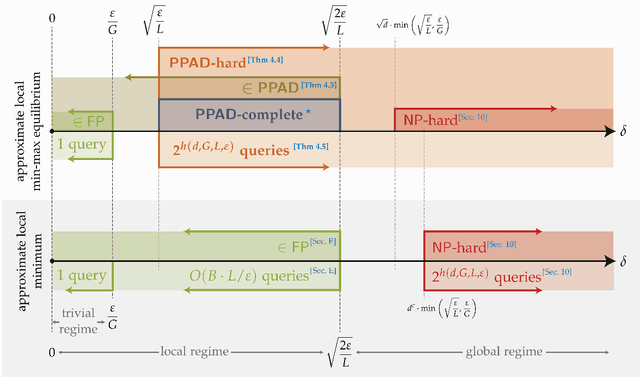
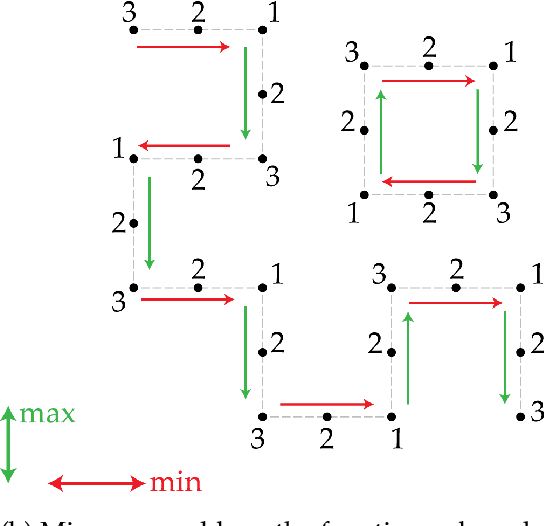
Despite its important applications in Machine Learning, min-max optimization of nonconvex-nonconcave objectives remains elusive. Not only are there no known first-order methods converging even to approximate local min-max points, but the computational complexity of identifying them is also poorly understood. In this paper, we provide a characterization of the computational complexity of the problem, as well as of the limitations of first-order methods in constrained min-max optimization problems with nonconvex-nonconcave objectives and linear constraints. As a warm-up, we show that, even when the objective is a Lipschitz and smooth differentiable function, deciding whether a min-max point exists, in fact even deciding whether an approximate min-max point exists, is NP-hard. More importantly, we show that an approximate local min-max point of large enough approximation is guaranteed to exist, but finding one such point is PPAD-complete. The same is true of computing an approximate fixed point of Gradient Descent/Ascent. An important byproduct of our proof is to establish an unconditional hardness result in the Nemirovsky-Yudin model. We show that, given oracle access to some function $f : P \to [-1, 1]$ and its gradient $\nabla f$, where $P \subseteq [0, 1]^d$ is a known convex polytope, every algorithm that finds a $\varepsilon$-approximate local min-max point needs to make a number of queries that is exponential in at least one of $1/\varepsilon$, $L$, $G$, or $d$, where $L$ and $G$ are respectively the smoothness and Lipschitzness of $f$ and $d$ is the dimension. This comes in sharp contrast to minimization problems, where finding approximate local minima in the same setting can be done with Projected Gradient Descent using $O(L/\varepsilon)$ many queries. Our result is the first to show an exponential separation between these two fundamental optimization problems.

Convergence to Second-Order Stationarity for Non-negative Matrix Factorization: Provably and Concurrently

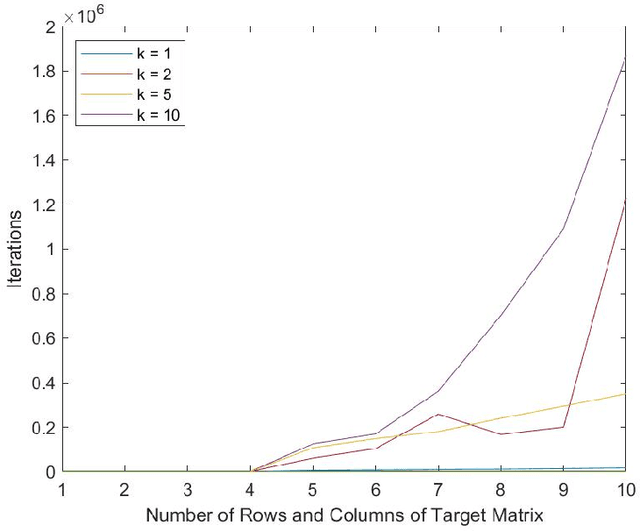
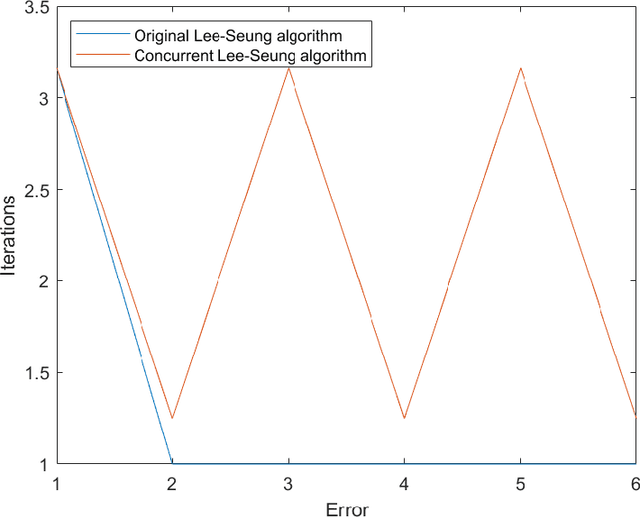
Non-negative matrix factorization (NMF) is a fundamental non-convex optimization problem with numerous applications in Machine Learning (music analysis, document clustering, speech-source separation etc). Despite having received extensive study, it is poorly understood whether or not there exist natural algorithms that can provably converge to a local minimum. Part of the reason is because the objective is heavily symmetric and its gradient is not Lipschitz. In this paper we define a multiplicative weight update type dynamics (modification of the seminal Lee-Seung algorithm) that runs concurrently and provably avoids saddle points (first order stationary points that are not second order). Our techniques combine tools from dynamical systems such as stability and exploit the geometry of the NMF objective by reducing the standard NMF formulation over the non-negative orthant to a new formulation over (a scaled) simplex. An important advantage of our method is the use of concurrent updates, which permits implementations in parallel computing environments.