Stephen Roberts
Mosquito detection with low-cost smartphones: data acquisition for malaria research
Dec 06, 2017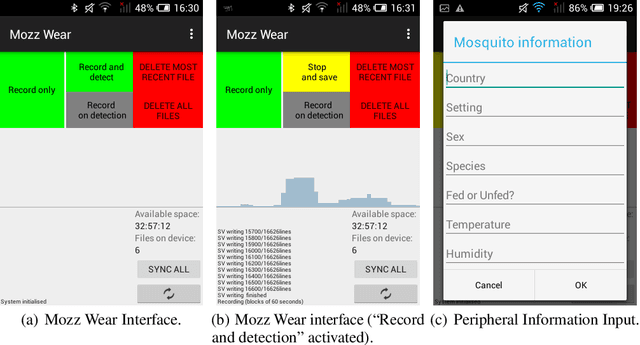
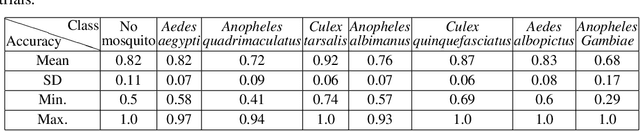
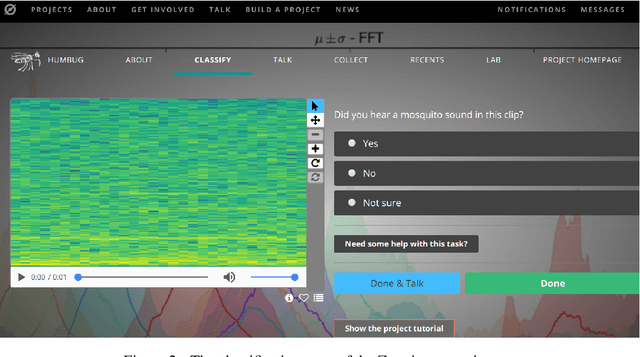
Abstract:Mosquitoes are a major vector for malaria, causing hundreds of thousands of deaths in the developing world each year. Not only is the prevention of mosquito bites of paramount importance to the reduction of malaria transmission cases, but understanding in more forensic detail the interplay between malaria, mosquito vectors, vegetation, standing water and human populations is crucial to the deployment of more effective interventions. Typically the presence and detection of malaria-vectoring mosquitoes is only quantified by hand-operated insect traps or signified by the diagnosis of malaria. If we are to gather timely, large-scale data to improve this situation, we need to automate the process of mosquito detection and classification as much as possible. In this paper, we present a candidate mobile sensing system that acts as both a portable early warning device and an automatic acoustic data acquisition pipeline to help fuel scientific inquiry and policy. The machine learning algorithm that powers the mobile system achieves excellent off-line multi-species detection performance while remaining computationally efficient. Further, we have conducted preliminary live mosquito detection tests using low-cost mobile phones and achieved promising results. The deployment of this system for field usage in Southeast Asia and Africa is planned in the near future. In order to accelerate processing of field recordings and labelling of collected data, we employ a citizen science platform in conjunction with automated methods, the former implemented using the Zooniverse platform, allowing crowdsourcing on a grand scale.
Novel Exploration Techniques (NETs) for Malaria Policy Interventions
Dec 01, 2017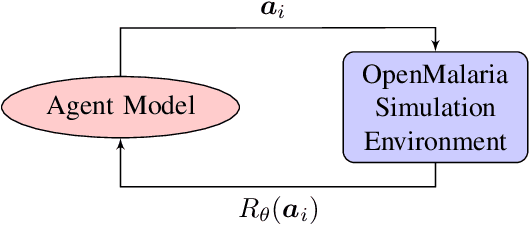
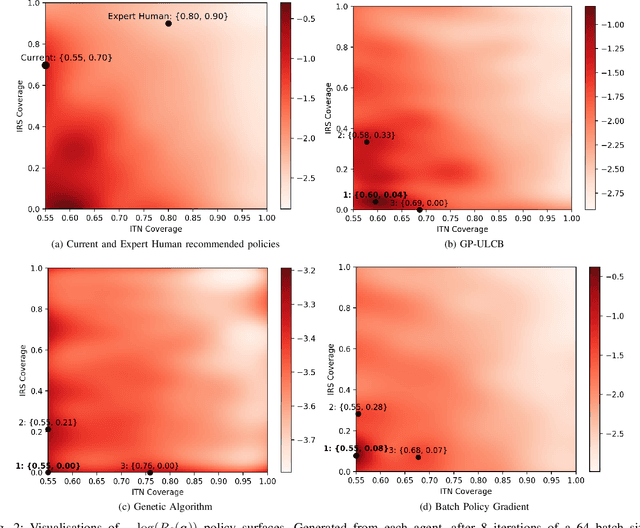

Abstract:The task of decision-making under uncertainty is daunting, especially for problems which have significant complexity. Healthcare policy makers across the globe are facing problems under challenging constraints, with limited tools to help them make data driven decisions. In this work we frame the process of finding an optimal malaria policy as a stochastic multi-armed bandit problem, and implement three agent based strategies to explore the policy space. We apply a Gaussian Process regression to the findings of each agent, both for comparison and to account for stochastic results from simulating the spread of malaria in a fixed population. The generated policy spaces are compared with published results to give a direct reference with human expert decisions for the same simulated population. Our novel approach provides a powerful resource for policy makers, and a platform which can be readily extended to capture future more nuanced policy spaces.
Riemannian tangent space mapping and elastic net regularization for cost-effective EEG markers of brain atrophy in Alzheimer's disease
Nov 22, 2017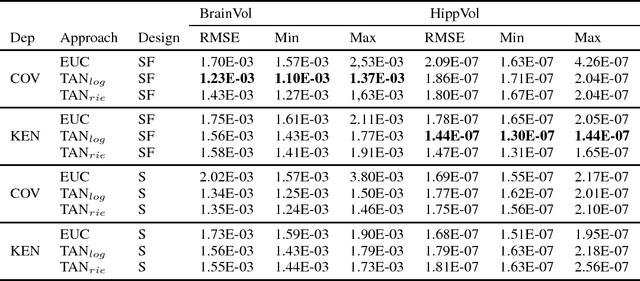
Abstract:The diagnosis of Alzheimer's disease (AD) in routine clinical practice is most commonly based on subjective clinical interpretations. Quantitative electroencephalography (QEEG) measures have been shown to reflect neurodegenerative processes in AD and might qualify as affordable and thereby widely available markers to facilitate the objectivization of AD assessment. Here, we present a novel framework combining Riemannian tangent space mapping and elastic net regression for the development of brain atrophy markers. While most AD QEEG studies are based on small sample sizes and psychological test scores as outcome measures, here we train and test our models using data of one of the largest prospective EEG AD trials ever conducted, including MRI biomarkers of brain atrophy.
Entropic Determinants
Sep 08, 2017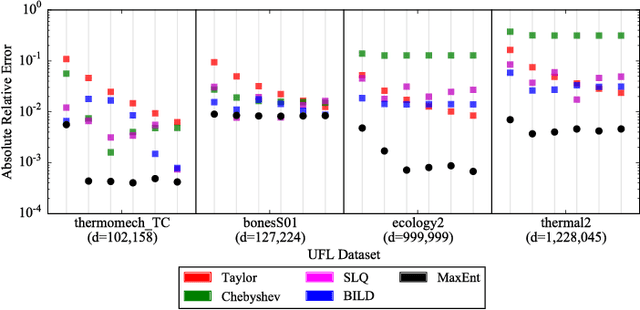
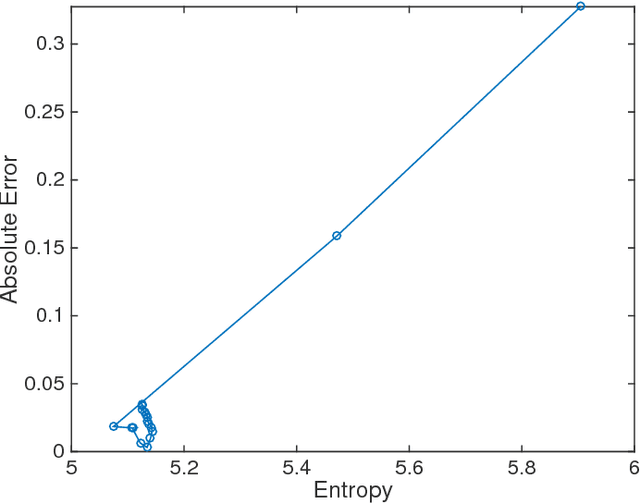
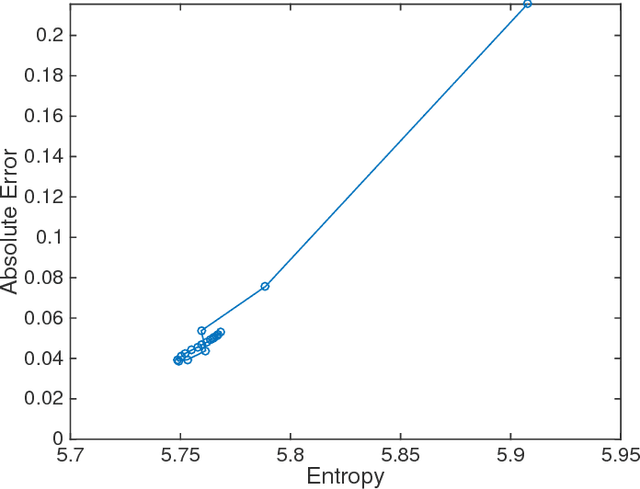
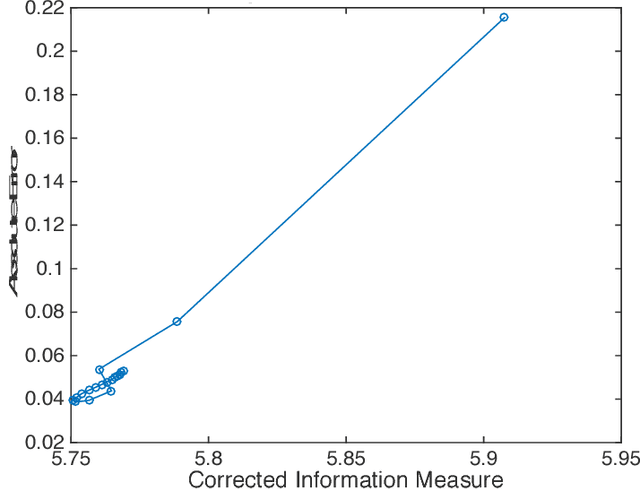
Abstract:The ability of many powerful machine learning algorithms to deal with large data sets without compromise is often hampered by computationally expensive linear algebra tasks, of which calculating the log determinant is a canonical example. In this paper we demonstrate the optimality of Maximum Entropy methods in approximating such calculations. We prove the equivalence between mean value constraints and sample expectations in the big data limit, that Covariance matrix eigenvalue distributions can be completely defined by moment information and that the reduction of the self entropy of a maximum entropy proposal distribution, achieved by adding more moments reduces the KL divergence between the proposal and true eigenvalue distribution. We empirically verify our results on a variety of SparseSuite matrices and establish best practices.
Mosquito Detection with Neural Networks: The Buzz of Deep Learning
May 15, 2017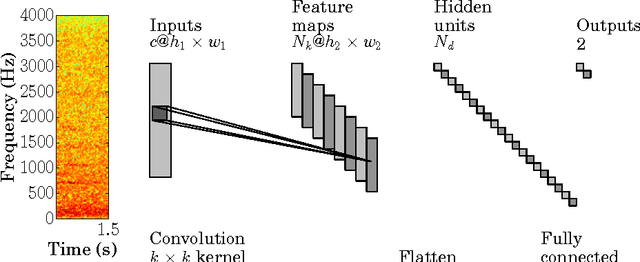

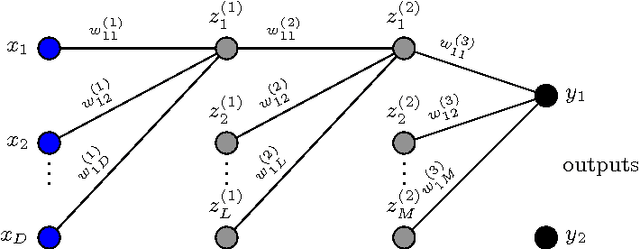
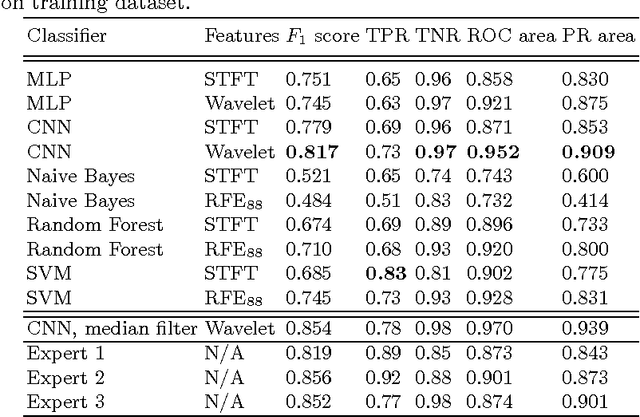
Abstract:Many real-world time-series analysis problems are characterised by scarce data. Solutions typically rely on hand-crafted features extracted from the time or frequency domain allied with classification or regression engines which condition on this (often low-dimensional) feature vector. The huge advances enjoyed by many application domains in recent years have been fuelled by the use of deep learning architectures trained on large data sets. This paper presents an application of deep learning for acoustic event detection in a challenging, data-scarce, real-world problem. Our candidate challenge is to accurately detect the presence of a mosquito from its acoustic signature. We develop convolutional neural networks (CNNs) operating on wavelet transformations of audio recordings. Furthermore, we interrogate the network's predictive power by visualising statistics of network-excitatory samples. These visualisations offer a deep insight into the relative informativeness of components in the detection problem. We include comparisons with conventional classifiers, conditioned on both hand-tuned and generic features, to stress the strength of automatic deep feature learning. Detection is achieved with performance metrics significantly surpassing those of existing algorithmic methods, as well as marginally exceeding those attained by individual human experts.
Entropic Trace Estimates for Log Determinants
Apr 24, 2017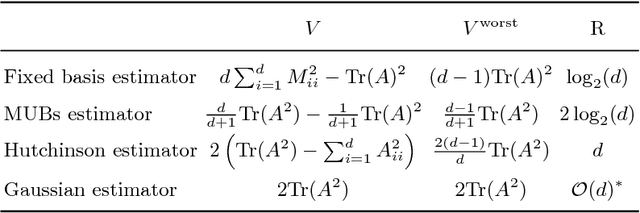
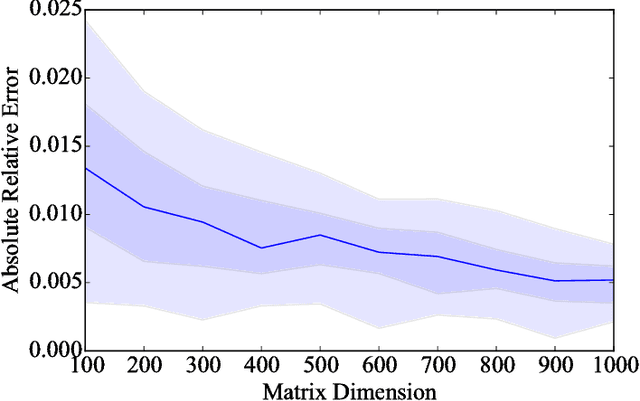
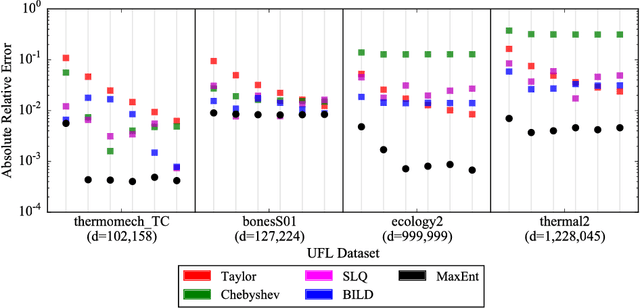
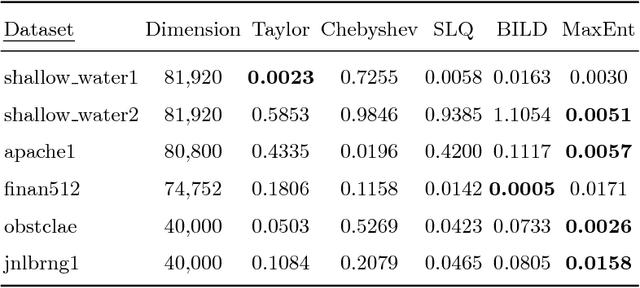
Abstract:The scalable calculation of matrix determinants has been a bottleneck to the widespread application of many machine learning methods such as determinantal point processes, Gaussian processes, generalised Markov random fields, graph models and many others. In this work, we estimate log determinants under the framework of maximum entropy, given information in the form of moment constraints from stochastic trace estimation. The estimates demonstrate a significant improvement on state-of-the-art alternative methods, as shown on a wide variety of UFL sparse matrices. By taking the example of a general Markov random field, we also demonstrate how this approach can significantly accelerate inference in large-scale learning methods involving the log determinant.
Bayesian Inference of Log Determinants
Apr 05, 2017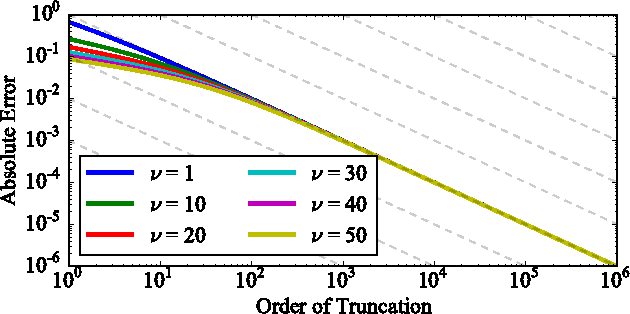
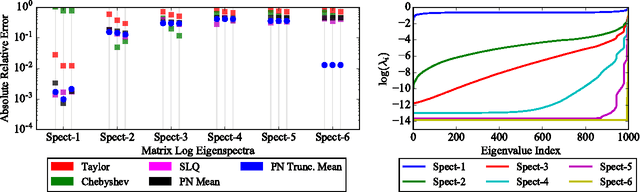
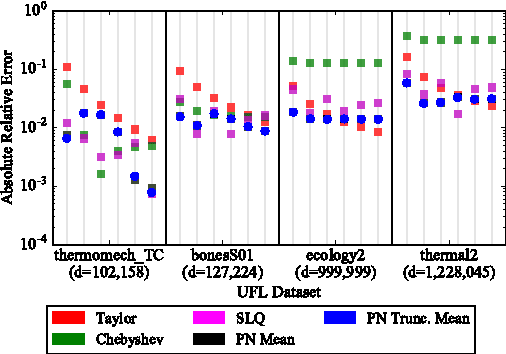
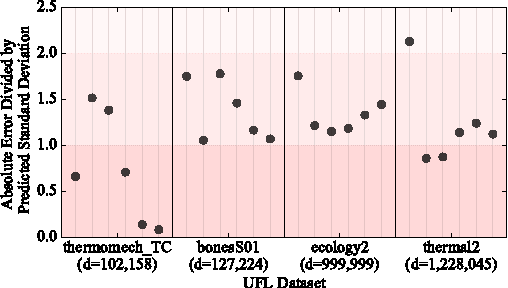
Abstract:The log-determinant of a kernel matrix appears in a variety of machine learning problems, ranging from determinantal point processes and generalized Markov random fields, through to the training of Gaussian processes. Exact calculation of this term is often intractable when the size of the kernel matrix exceeds a few thousand. In the spirit of probabilistic numerics, we reinterpret the problem of computing the log-determinant as a Bayesian inference problem. In particular, we combine prior knowledge in the form of bounds from matrix theory and evidence derived from stochastic trace estimation to obtain probabilistic estimates for the log-determinant and its associated uncertainty within a given computational budget. Beyond its novelty and theoretic appeal, the performance of our proposal is competitive with state-of-the-art approaches to approximating the log-determinant, while also quantifying the uncertainty due to budget-constrained evidence.
String and Membrane Gaussian Processes
Aug 19, 2016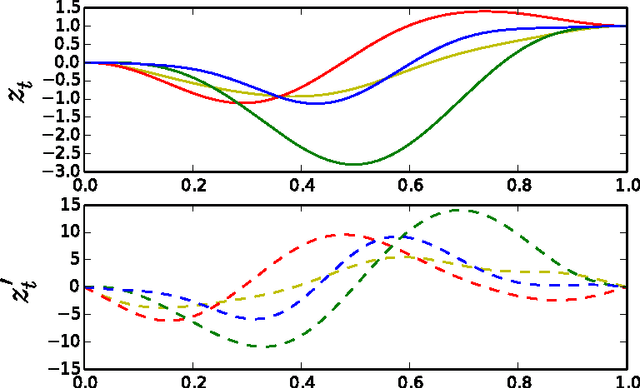
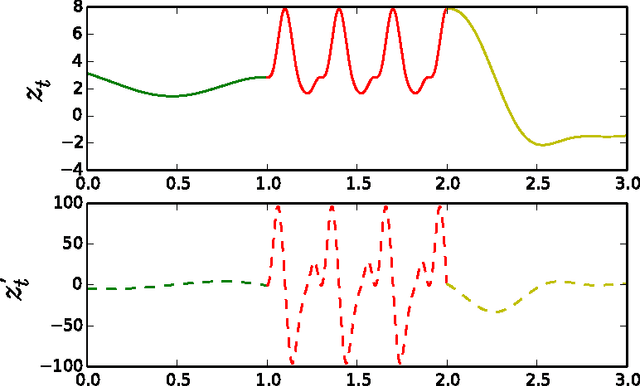
Abstract:In this paper we introduce a novel framework for making exact nonparametric Bayesian inference on latent functions, that is particularly suitable for Big Data tasks. Firstly, we introduce a class of stochastic processes we refer to as string Gaussian processes (string GPs), which are not to be mistaken for Gaussian processes operating on text. We construct string GPs so that their finite-dimensional marginals exhibit suitable local conditional independence structures, which allow for scalable, distributed, and flexible nonparametric Bayesian inference, without resorting to approximations, and while ensuring some mild global regularity constraints. Furthermore, string GP priors naturally cope with heterogeneous input data, and the gradient of the learned latent function is readily available for explanatory analysis. Secondly, we provide some theoretical results relating our approach to the standard GP paradigm. In particular, we prove that some string GPs are Gaussian processes, which provides a complementary global perspective on our framework. Finally, we derive a scalable and distributed MCMC scheme for supervised learning tasks under string GP priors. The proposed MCMC scheme has computational time complexity $\mathcal{O}(N)$ and memory requirement $\mathcal{O}(dN)$, where $N$ is the data size and $d$ the dimension of the input space. We illustrate the efficacy of the proposed approach on several synthetic and real-world datasets, including a dataset with $6$ millions input points and $8$ attributes.
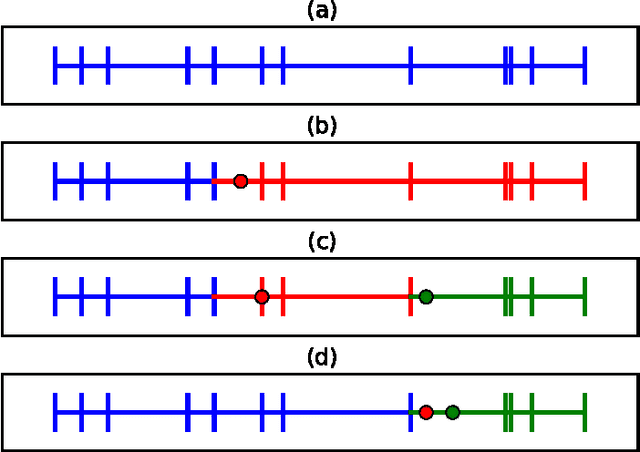
Blitzkriging: Kronecker-structured Stochastic Gaussian Processes
Oct 31, 2015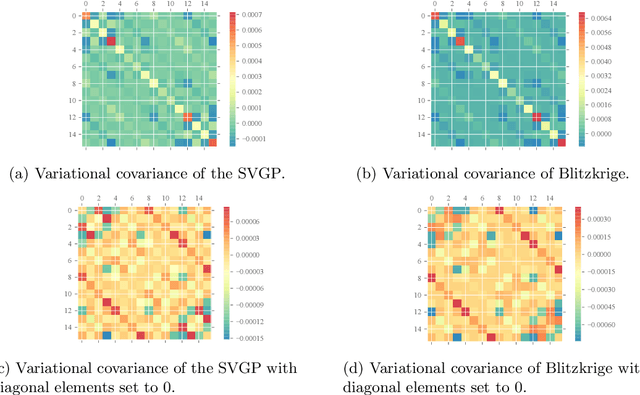

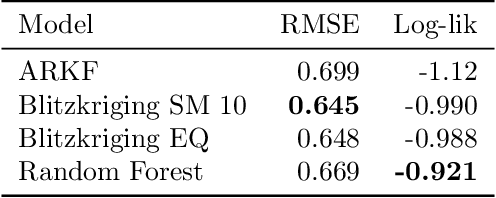
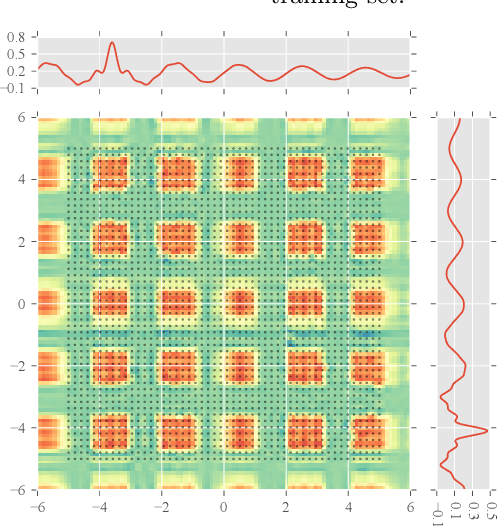
Abstract:We present Blitzkriging, a new approach to fast inference for Gaussian processes, applicable to regression, optimisation and classification. State-of-the-art (stochastic) inference for Gaussian processes on very large datasets scales cubically in the number of 'inducing inputs', variables introduced to factorise the model. Blitzkriging shares state-of-the-art scaling with data, but reduces the scaling in the number of inducing points to approximately linear. Further, in contrast to other methods, Blitzkriging: does not force the data to conform to any particular structure (including grid-like); reduces reliance on error-prone optimisation of inducing point locations; and is able to learn rich (covariance) structure from the data. We demonstrate the benefits of our approach on real data in regression, time-series prediction and signal-interpolation experiments.
Generalized Spectral Kernels
Oct 09, 2015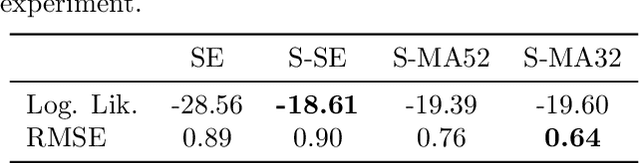
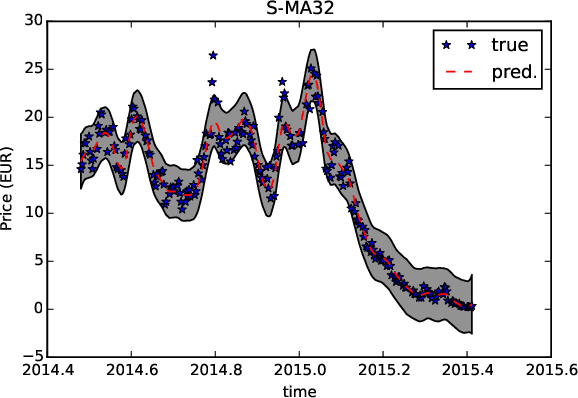
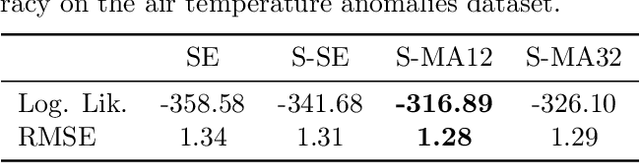
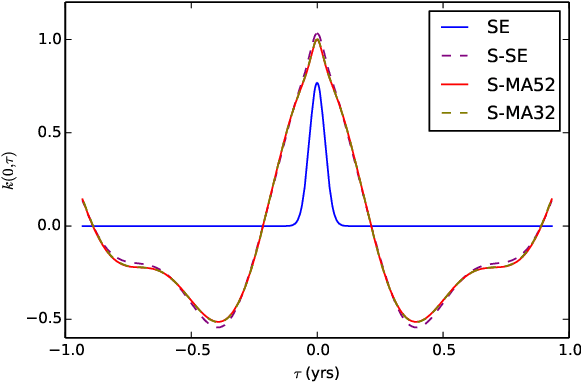
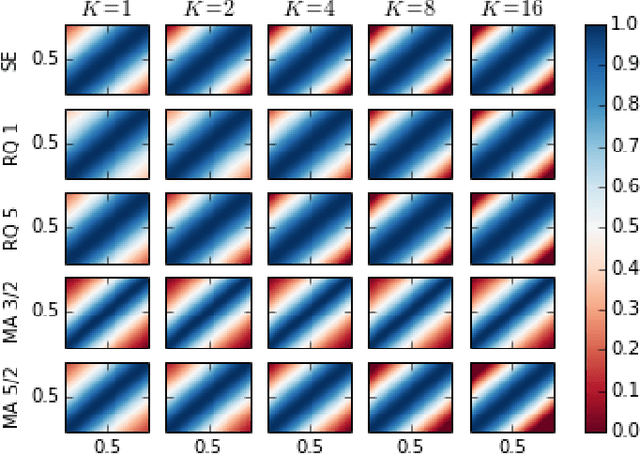
Abstract:In this paper we propose a family of tractable kernels that is dense in the family of bounded positive semi-definite functions (i.e. can approximate any bounded kernel with arbitrary precision). We start by discussing the case of stationary kernels, and propose a family of spectral kernels that extends existing approaches such as spectral mixture kernels and sparse spectrum kernels. Our extension has two primary advantages. Firstly, unlike existing spectral approaches that yield infinite differentiability, the kernels we introduce allow learning the degree of differentiability of the latent function in Gaussian process (GP) models and functions in the reproducing kernel Hilbert space (RKHS) in other kernel methods. Secondly, we show that some of the kernels we propose require fewer parameters than existing spectral kernels for the same accuracy, thereby leading to faster and more robust inference. Finally, we generalize our approach and propose a flexible and tractable family of spectral kernels that we prove can approximate any continuous bounded nonstationary kernel.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge