LeanML: A Design Pattern To Slash Avoidable Wastes in Machine Learning Projects

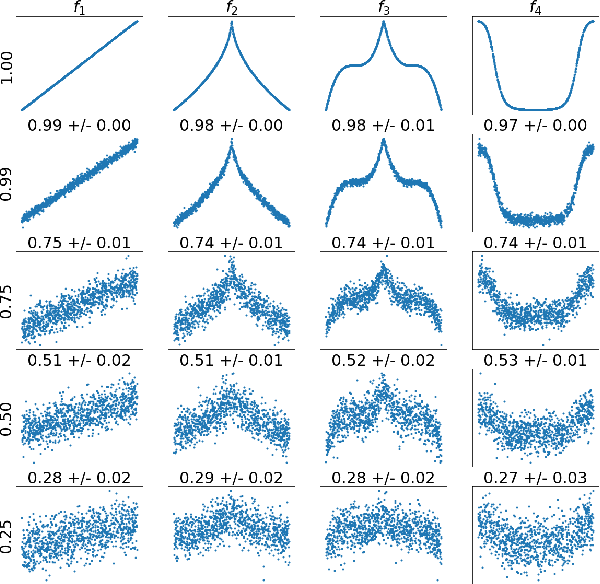
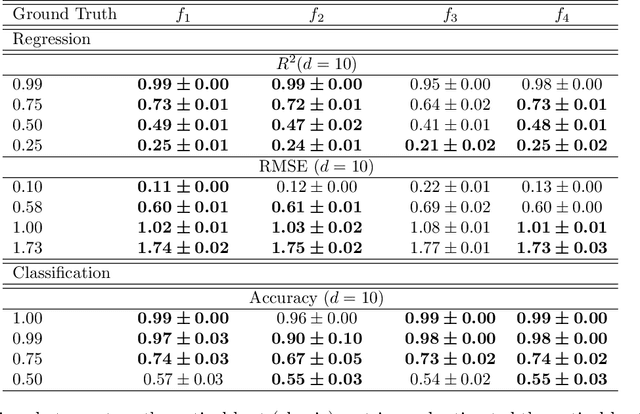
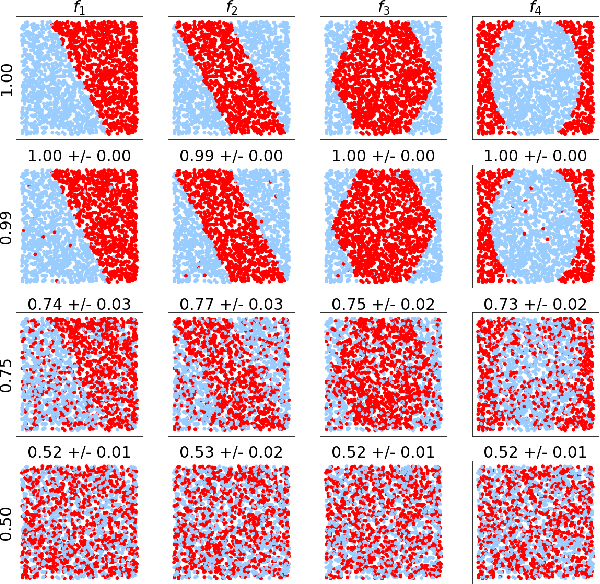
We introduce the first application of the lean methodology to machine learning projects. Similar to lean startups and lean manufacturing, we argue that lean machine learning (LeanML) can drastically slash avoidable wastes in commercial machine learning projects, reduce the business risk in investing in machine learning capabilities and, in so doing, further democratize access to machine learning. The lean design pattern we propose in this paper is based on two realizations. First, it is possible to estimate the best performance one may achieve when predicting an outcome $y \in \mathcal{Y}$ using a given set of explanatory variables $x \in \mathcal{X}$, for a wide range of performance metrics, and without training any predictive model. Second, doing so is considerably easier, faster, and cheaper than learning the best predictive model. We derive formulae expressing the best $R^2$, MSE, classification accuracy, and log-likelihood per observation achievable when using $x$ to predict $y$ as a function of the mutual information $I\left(y; x\right)$, and possibly a measure of the variability of $y$ (e.g. its Shannon entropy in the case of classification accuracy, and its variance in the case regression MSE). We illustrate the efficacy of the LeanML design pattern on a wide range of regression and classification problems, synthetic and real-life.

Inductive Mutual Information Estimation: A Convex Maximum-Entropy Copula Approach

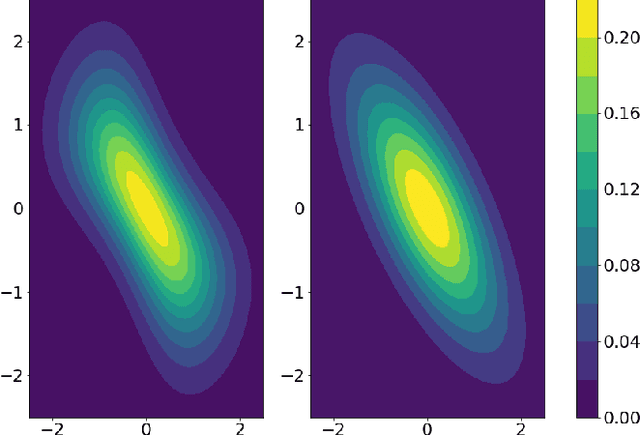
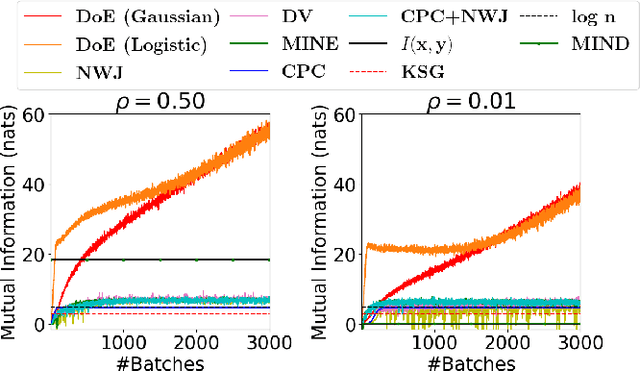
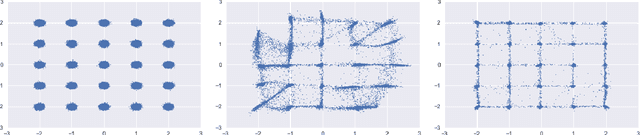
We propose a novel estimator of the mutual information between two ordinal vectors $x$ and $y$. Our approach is inductive (as opposed to deductive) in that it depends on the data generating distribution solely through some nonparametric properties revealing associations in the data, and does not require having enough data to fully characterize the true joint distributions $P_{x, y}$. Specifically, our approach consists of (i) noting that $I\left(y; x\right) = I\left(u_y; u_x\right)$ where $u_y$ and $u_x$ are the \emph{copula-uniform dual representations} of $y$ and $x$ (i.e. their images under the probability integral transform), and (ii) estimating the copula entropies $h\left(u_y\right)$, $h\left(u_x\right)$ and $h\left(u_y, u_x\right)$ by solving a maximum-entropy problem over the space of copula densities under a constraint of the type $\alpha_m = E\left[\phi_m(u_y, u_x)\right]$. We prove that, so long as the constraint is feasible, this problem admits a unique solution, it is in the exponential family, and it can be learned by solving a convex optimization problem. The resulting estimator, which we denote MIND, is marginal-invariant, always non-negative, unbounded for any sample size $n$, consistent, has MSE rate $O(1/n)$, and is more data-efficient than competing approaches. Beyond mutual information estimation, we illustrate that our approach may be used to mitigate mode collapse in GANs by maximizing the entropy of the copula of fake samples, a model we refer to as Copula Entropy Regularized GAN (CER-GAN).

String and Membrane Gaussian Processes

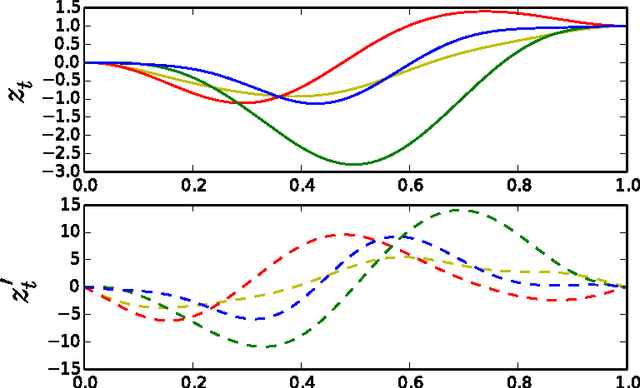
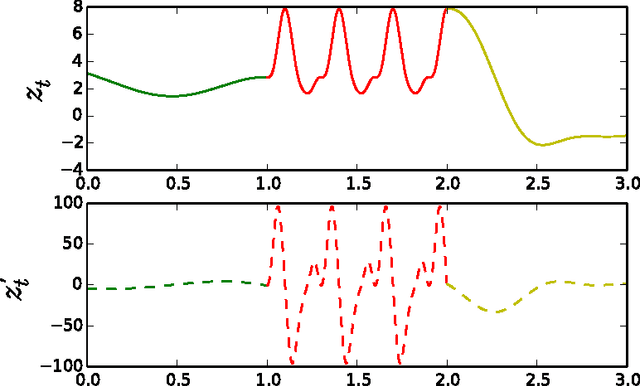
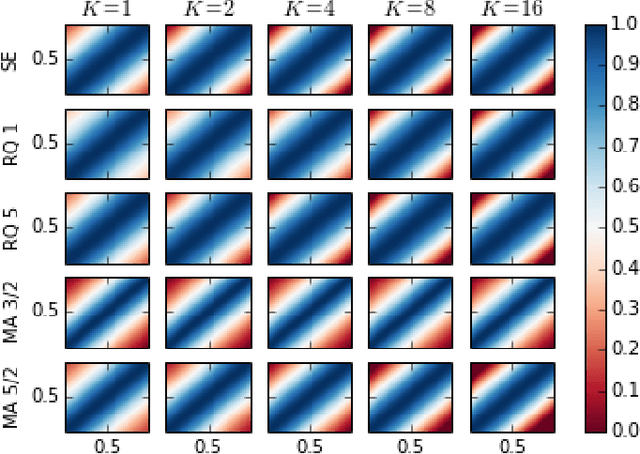
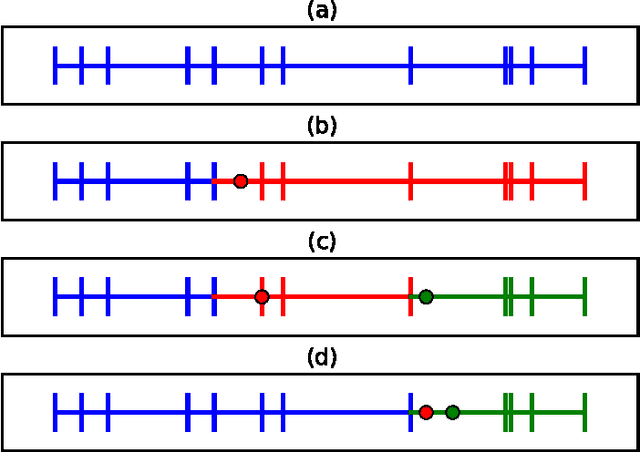
In this paper we introduce a novel framework for making exact nonparametric Bayesian inference on latent functions, that is particularly suitable for Big Data tasks. Firstly, we introduce a class of stochastic processes we refer to as string Gaussian processes (string GPs), which are not to be mistaken for Gaussian processes operating on text. We construct string GPs so that their finite-dimensional marginals exhibit suitable local conditional independence structures, which allow for scalable, distributed, and flexible nonparametric Bayesian inference, without resorting to approximations, and while ensuring some mild global regularity constraints. Furthermore, string GP priors naturally cope with heterogeneous input data, and the gradient of the learned latent function is readily available for explanatory analysis. Secondly, we provide some theoretical results relating our approach to the standard GP paradigm. In particular, we prove that some string GPs are Gaussian processes, which provides a complementary global perspective on our framework. Finally, we derive a scalable and distributed MCMC scheme for supervised learning tasks under string GP priors. The proposed MCMC scheme has computational time complexity $\mathcal{O}(N)$ and memory requirement $\mathcal{O}(dN)$, where $N$ is the data size and $d$ the dimension of the input space. We illustrate the efficacy of the proposed approach on several synthetic and real-world datasets, including a dataset with $6$ millions input points and $8$ attributes.

Stochastic Portfolio Theory: A Machine Learning Perspective

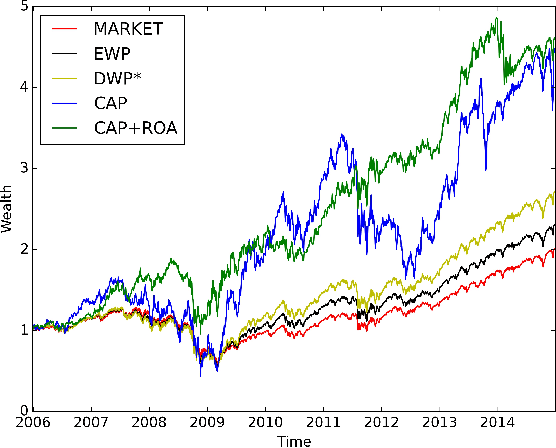
In this paper we propose a novel application of Gaussian processes (GPs) to financial asset allocation. Our approach is deeply rooted in Stochastic Portfolio Theory (SPT), a stochastic analysis framework introduced by Robert Fernholz that aims at flexibly analysing the performance of certain investment strategies in stock markets relative to benchmark indices. In particular, SPT has exhibited some investment strategies based on company sizes that, under realistic assumptions, outperform benchmark indices with probability 1 over certain time horizons. Galvanised by this result, we consider the inverse problem that consists of learning (from historical data) an optimal investment strategy based on any given set of trading characteristics, and using a user-specified optimality criterion that may go beyond outperforming a benchmark index. Although this inverse problem is of the utmost interest to investment management practitioners, it can hardly be tackled using the SPT framework. We show that our machine learning approach learns investment strategies that considerably outperform existing SPT strategies in the US stock market.

p-Markov Gaussian Processes for Scalable and Expressive Online Bayesian Nonparametric Time Series Forecasting

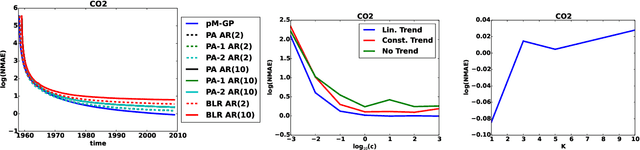
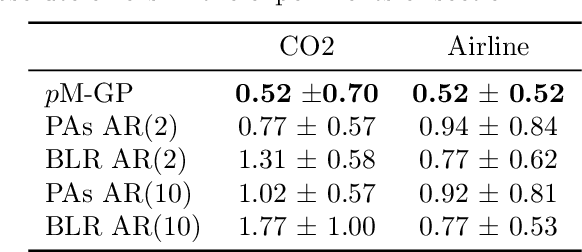
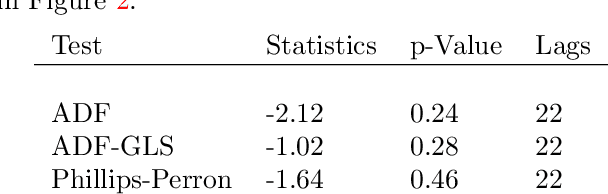
In this paper we introduce a novel online time series forecasting model we refer to as the pM-GP filter. We show that our model is equivalent to Gaussian process regression, with the advantage that both online forecasting and online learning of the hyper-parameters have a constant (rather than cubic) time complexity and a constant (rather than squared) memory requirement in the number of observations, without resorting to approximations. Moreover, the proposed model is expressive in that the family of covariance functions of the implied latent process, namely the spectral Matern kernels, have recently been proven to be capable of approximating arbitrarily well any translation-invariant covariance function. The benefit of our approach compared to competing models is demonstrated using experiments on several real-life datasets.

Generalized Spectral Kernels

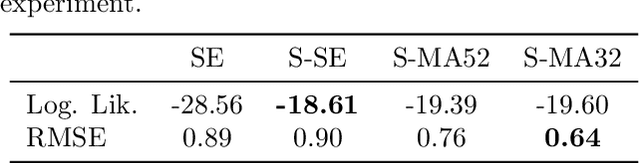
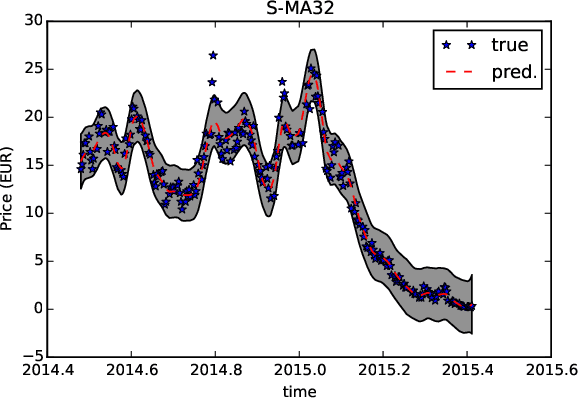
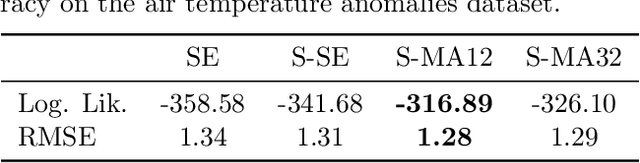
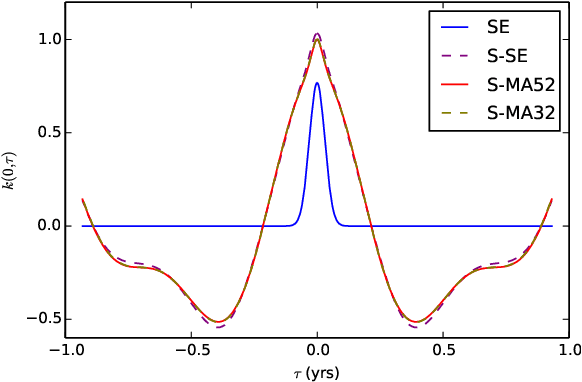
In this paper we propose a family of tractable kernels that is dense in the family of bounded positive semi-definite functions (i.e. can approximate any bounded kernel with arbitrary precision). We start by discussing the case of stationary kernels, and propose a family of spectral kernels that extends existing approaches such as spectral mixture kernels and sparse spectrum kernels. Our extension has two primary advantages. Firstly, unlike existing spectral approaches that yield infinite differentiability, the kernels we introduce allow learning the degree of differentiability of the latent function in Gaussian process (GP) models and functions in the reproducing kernel Hilbert space (RKHS) in other kernel methods. Secondly, we show that some of the kernels we propose require fewer parameters than existing spectral kernels for the same accuracy, thereby leading to faster and more robust inference. Finally, we generalize our approach and propose a flexible and tractable family of spectral kernels that we prove can approximate any continuous bounded nonstationary kernel.

String Gaussian Process Kernels

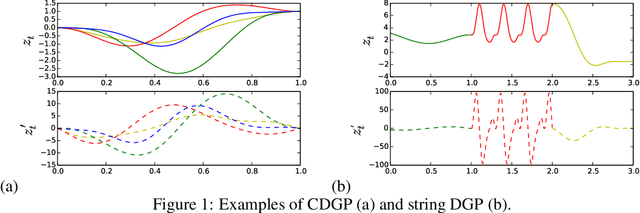
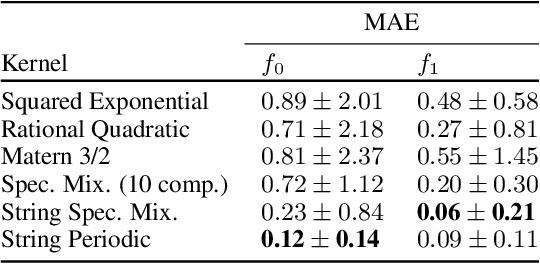
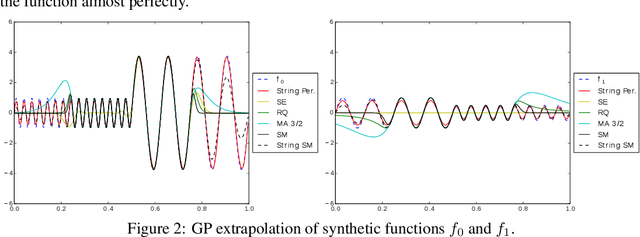
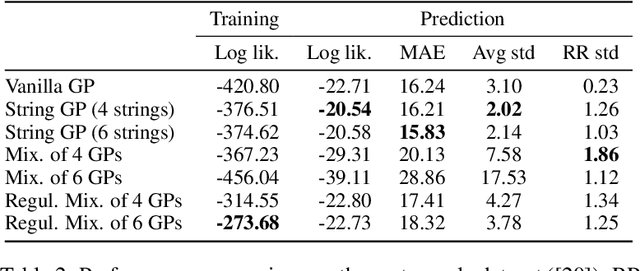
We introduce a new class of nonstationary kernels, which we derive as covariance functions of a novel family of stochastic processes we refer to as string Gaussian processes (string GPs). We construct string GPs to allow for multiple types of local patterns in the data, while ensuring a mild global regularity condition. In this paper, we illustrate the efficacy of the approach using synthetic data and demonstrate that the model outperforms competing approaches on well studied, real-life datasets that exhibit nonstationary features.

Scalable Nonparametric Bayesian Inference on Point Processes with Gaussian Processes

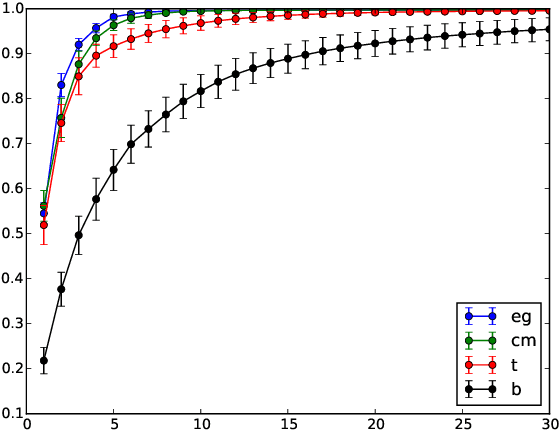
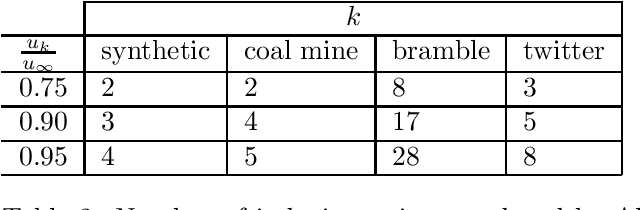
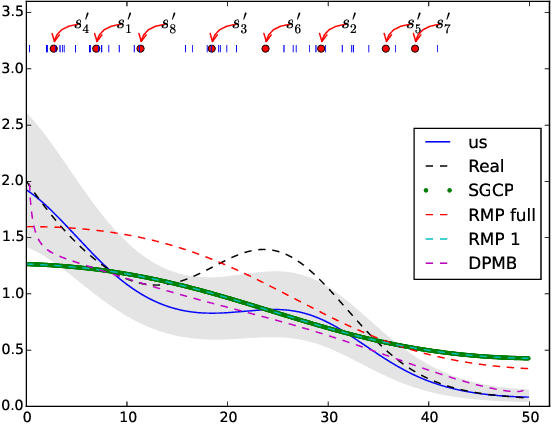
In this paper we propose the first non-parametric Bayesian model using Gaussian Processes to make inference on Poisson Point Processes without resorting to gridding the domain or to introducing latent thinning points. Unlike competing models that scale cubically and have a squared memory requirement in the number of data points, our model has a linear complexity and memory requirement. We propose an MCMC sampler and show that our model is faster, more accurate and generates less correlated samples than competing models on both synthetic and real-life data. Finally, we show that our model easily handles data sizes not considered thus far by alternate approaches.