Stephen Roberts
Transfer Ranking in Finance: Applications to Cross-Sectional Momentum with Data Scarcity
Aug 24, 2022
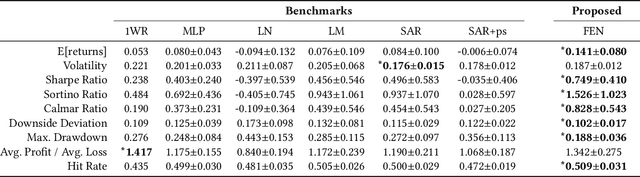
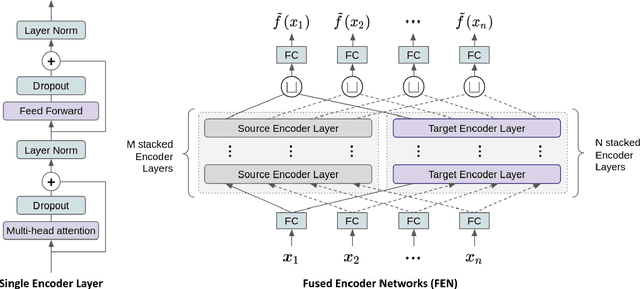
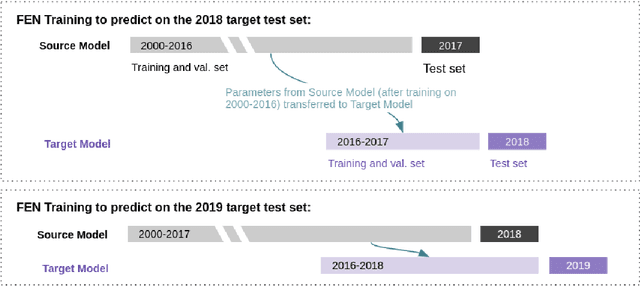
Abstract:Cross-sectional strategies are a classical and popular trading style, with recent high performing variants incorporating sophisticated neural architectures. While these strategies have been applied successfully to data-rich settings involving mature assets with long histories, deploying them on instruments with limited samples generally produce over-fitted models with degraded performance. In this paper, we introduce Fused Encoder Networks -- a novel and hybrid parameter-sharing transfer ranking model. The model fuses information extracted using an encoder-attention module operated on a source dataset with a similar but separate module focused on a smaller target dataset of interest. This mitigates the issue of models with poor generalisability that are a consequence of training on scarce target data. Additionally, the self-attention mechanism enables interactions among instruments to be accounted for, not just at the loss level during model training, but also at inference time. Focusing on momentum applied to the top ten cryptocurrencies by market capitalisation as a demonstrative use-case, the Fused Encoder Networks outperforms the reference benchmarks on most performance measures, delivering a three-fold boost in the Sharpe ratio over classical momentum as well as an improvement of approximately 50% against the best benchmark model without transaction costs. It continues outperforming baselines even after accounting for the high transaction costs associated with trading cryptocurrencies.
The ACM Multimedia 2022 Computational Paralinguistics Challenge: Vocalisations, Stuttering, Activity, & Mosquitoes
May 13, 2022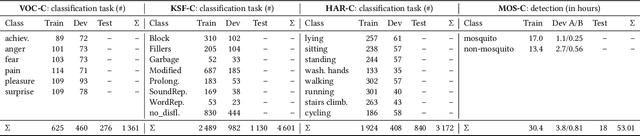
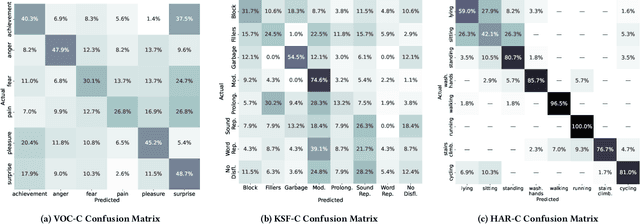

Abstract:The ACM Multimedia 2022 Computational Paralinguistics Challenge addresses four different problems for the first time in a research competition under well-defined conditions: In the Vocalisations and Stuttering Sub-Challenges, a classification on human non-verbal vocalisations and speech has to be made; the Activity Sub-Challenge aims at beyond-audio human activity recognition from smartwatch sensor data; and in the Mosquitoes Sub-Challenge, mosquitoes need to be detected. We describe the Sub-Challenges, baseline feature extraction, and classifiers based on the usual ComPaRE and BoAW features, the auDeep toolkit, and deep feature extraction from pre-trained CNNs using the DeepSpectRum toolkit; in addition, we add end-to-end sequential modelling, and a log-mel-128-BNN.
Trading with the Momentum Transformer: An Intelligent and Interpretable Architecture
Dec 16, 2021Abstract:Deep learning architectures, specifically Deep Momentum Networks (DMNs) [1904.04912], have been found to be an effective approach to momentum and mean-reversion trading. However, some of the key challenges in recent years involve learning long-term dependencies, degradation of performance when considering returns net of transaction costs and adapting to new market regimes, notably during the SARS-CoV-2 crisis. Attention mechanisms, or Transformer-based architectures, are a solution to such challenges because they allow the network to focus on significant time steps in the past and longer-term patterns. We introduce the Momentum Transformer, an attention-based architecture which outperforms the benchmarks, and is inherently interpretable, providing us with greater insights into our deep learning trading strategy. Our model is an extension to the LSTM-based DMN, which directly outputs position sizing by optimising the network on a risk-adjusted performance metric, such as Sharpe ratio. We find an attention-LSTM hybrid Decoder-Only Temporal Fusion Transformer (TFT) style architecture is the best performing model. In terms of interpretability, we observe remarkable structure in the attention patterns, with significant peaks of importance at momentum turning points. The time series is thus segmented into regimes and the model tends to focus on previous time-steps in alike regimes. We find changepoint detection (CPD) [2105.13727], another technique for responding to regime change, can complement multi-headed attention, especially when we run CPD at multiple timescales. Through the addition of an interpretable variable selection network, we observe how CPD helps our model to move away from trading predominantly on daily returns data. We note that the model can intelligently switch between, and blend, classical strategies - basing its decision on patterns in the data.
A Bayesian take on option pricing with Gaussian processes
Dec 07, 2021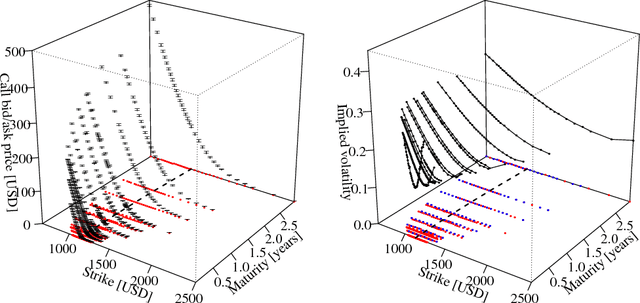
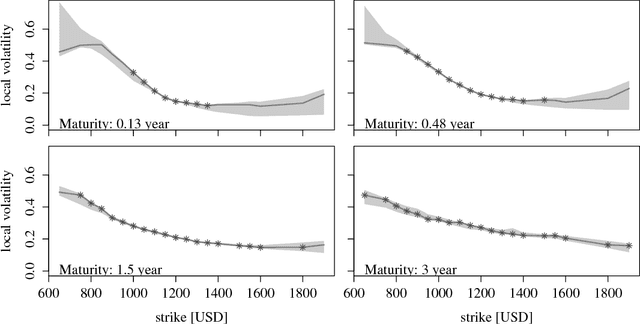
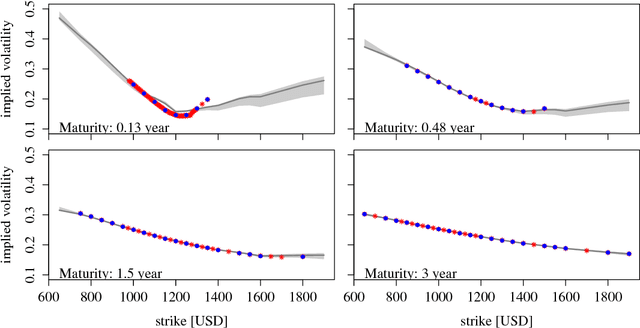
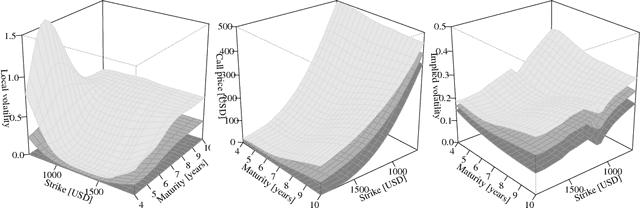
Abstract:Local volatility is a versatile option pricing model due to its state dependent diffusion coefficient. Calibration is, however, non-trivial as it involves both proposing a hypothesis model of the latent function and a method for fitting it to data. In this paper we present novel Bayesian inference with Gaussian process priors. We obtain a rich representation of the local volatility function with a probabilistic notion of uncertainty attached to the calibrate. We propose an inference algorithm and apply our approach to S&P 500 market data.
One-Shot Transfer Learning of Physics-Informed Neural Networks
Oct 21, 2021
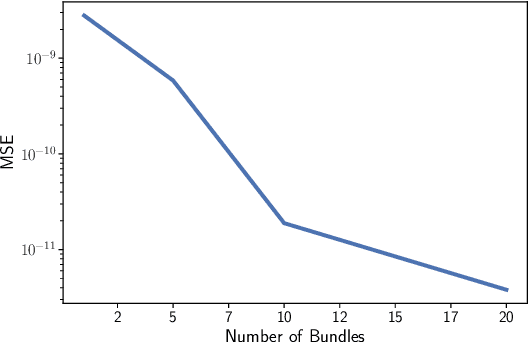
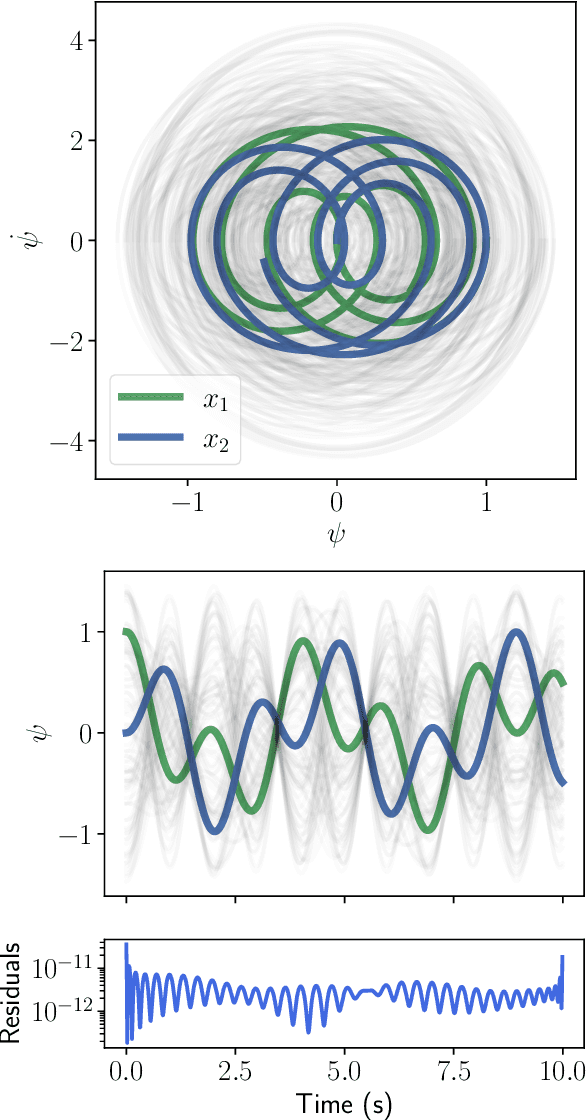
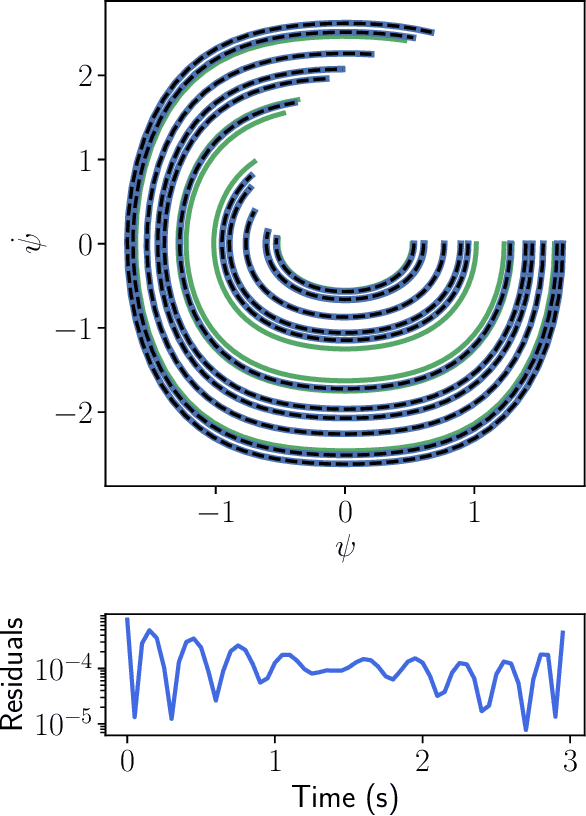
Abstract:Solving differential equations efficiently and accurately sits at the heart of progress in many areas of scientific research, from classical dynamical systems to quantum mechanics. There is a surge of interest in using Physics-Informed Neural Networks (PINNs) to tackle such problems as they provide numerous benefits over traditional numerical approaches. Despite their potential benefits for solving differential equations, transfer learning has been under explored. In this study, we present a general framework for transfer learning PINNs that results in one-shot inference for linear systems of both ordinary and partial differential equations. This means that highly accurate solutions to many unknown differential equations can be obtained instantaneously without retraining an entire network. We demonstrate the efficacy of the proposed deep learning approach by solving several real-world problems, such as first- and second-order linear ordinary equations, the Poisson equation, and the time-dependent Schrodinger complex-value partial differential equation.
Robust and Scalable SDE Learning: A Functional Perspective
Oct 11, 2021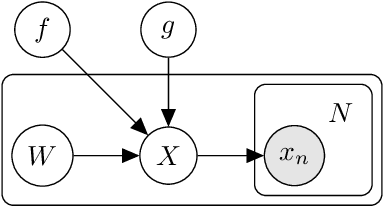
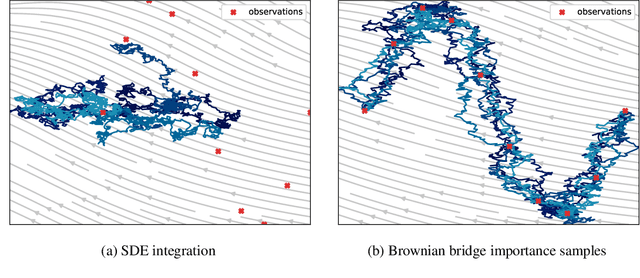
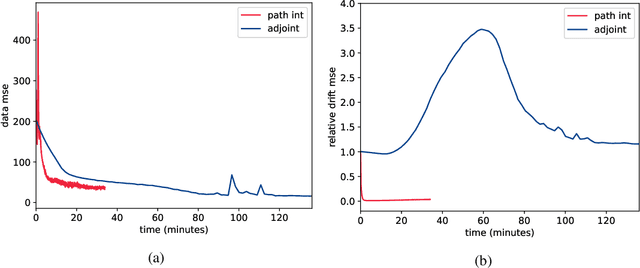
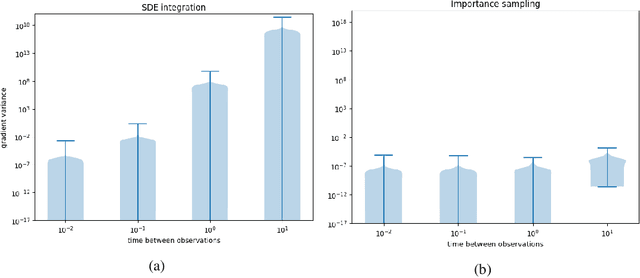
Abstract:Stochastic differential equations provide a rich class of flexible generative models, capable of describing a wide range of spatio-temporal processes. A host of recent work looks to learn data-representing SDEs, using neural networks and other flexible function approximators. Despite these advances, learning remains computationally expensive due to the sequential nature of SDE integrators. In this work, we propose an importance-sampling estimator for probabilities of observations of SDEs for the purposes of learning. Crucially, the approach we suggest does not rely on such integrators. The proposed method produces lower-variance gradient estimates compared to algorithms based on SDE integrators and has the added advantage of being embarrassingly parallelizable. This facilitates the effective use of large-scale parallel hardware for massive decreases in computation time.
Port-Hamiltonian Neural Networks for Learning Explicit Time-Dependent Dynamical Systems
Jul 16, 2021Abstract:Accurately learning the temporal behavior of dynamical systems requires models with well-chosen learning biases. Recent innovations embed the Hamiltonian and Lagrangian formalisms into neural networks and demonstrate a significant improvement over other approaches in predicting trajectories of physical systems. These methods generally tackle autonomous systems that depend implicitly on time or systems for which a control signal is known apriori. Despite this success, many real world dynamical systems are non-autonomous, driven by time-dependent forces and experience energy dissipation. In this study, we address the challenge of learning from such non-autonomous systems by embedding the port-Hamiltonian formalism into neural networks, a versatile framework that can capture energy dissipation and time-dependent control forces. We show that the proposed \emph{port-Hamiltonian neural network} can efficiently learn the dynamics of nonlinear physical systems of practical interest and accurately recover the underlying stationary Hamiltonian, time-dependent force, and dissipative coefficient. A promising outcome of our network is its ability to learn and predict chaotic systems such as the Duffing equation, for which the trajectories are typically hard to learn.
Tuning Mixed Input Hyperparameters on the Fly for Efficient Population Based AutoRL
Jun 30, 2021
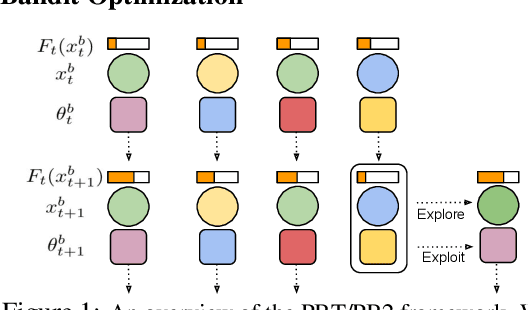
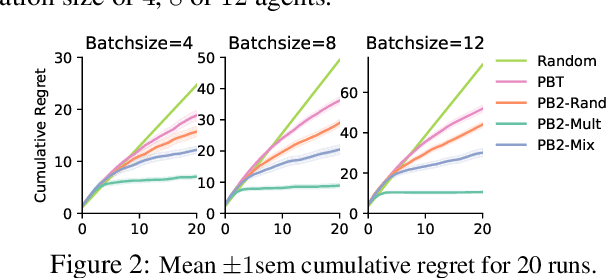
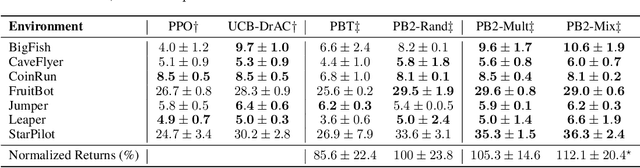
Abstract:Despite a series of recent successes in reinforcement learning (RL), many RL algorithms remain sensitive to hyperparameters. As such, there has recently been interest in the field of AutoRL, which seeks to automate design decisions to create more general algorithms. Recent work suggests that population based approaches may be effective AutoRL algorithms, by learning hyperparameter schedules on the fly. In particular, the PB2 algorithm is able to achieve strong performance in RL tasks by formulating online hyperparameter optimization as time varying GP-bandit problem, while also providing theoretical guarantees. However, PB2 is only designed to work for continuous hyperparameters, which severely limits its utility in practice. In this paper we introduce a new (provably) efficient hierarchical approach for optimizing both continuous and categorical variables, using a new time-varying bandit algorithm specifically designed for the population based training regime. We evaluate our approach on the challenging Procgen benchmark, where we show that explicitly modelling dependence between data augmentation and other hyperparameters improves generalization.
Slow Momentum with Fast Reversion: A Trading Strategy Using Deep Learning and Changepoint Detection
Jun 18, 2021Abstract:Momentum strategies are an important part of alternative investments and are at the heart of commodity trading advisors (CTAs). These strategies have however been found to have difficulties adjusting to rapid changes in market conditions, such as during the 2020 market crash. In particular, immediately after momentum turning points, where a trend reverses from an uptrend (downtrend) to a downtrend (uptrend), time-series momentum (TSMOM) strategies are prone to making bad bets. To improve the response to regime change, we introduce a novel approach, where we insert an online change-point detection (CPD) module into a Deep Momentum Network (DMN) [1904.04912] pipeline, which uses an LSTM deep-learning architecture to simultaneously learn both trend estimation and position sizing. Furthermore, our model is able to optimise the way in which it balances 1) a slow momentum strategy which exploits persisting trends, but does not overreact to localised price moves, and 2) a fast mean-reversion strategy regime by quickly flipping its position, then swapping it back again to exploit localised price moves. Our CPD module outputs a changepoint location and severity score, allowing our model to learn to respond to varying degrees of disequilibrium, or smaller and more localised changepoints, in a data driven manner. Using a portfolio of 50, liquid, continuous futures contracts over the period 1990-2020, the addition of the CPD module leads to an improvement in Sharpe ratio of one-third. Even more notably, this module is especially beneficial in periods of significant nonstationarity, and in particular, over the most recent years tested (2015-2020) the performance boost is approximately two-thirds. This is especially interesting as traditional momentum strategies have been underperforming in this period.
Can convolutional ResNets approximately preserve input distances? A frequency analysis perspective
Jun 17, 2021
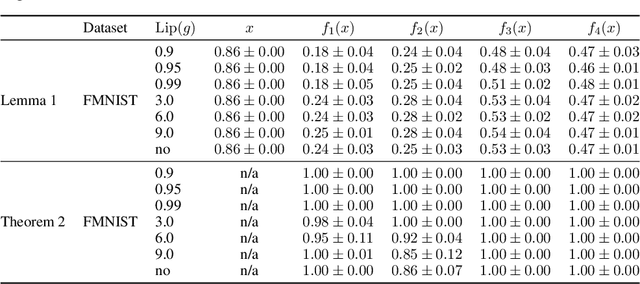

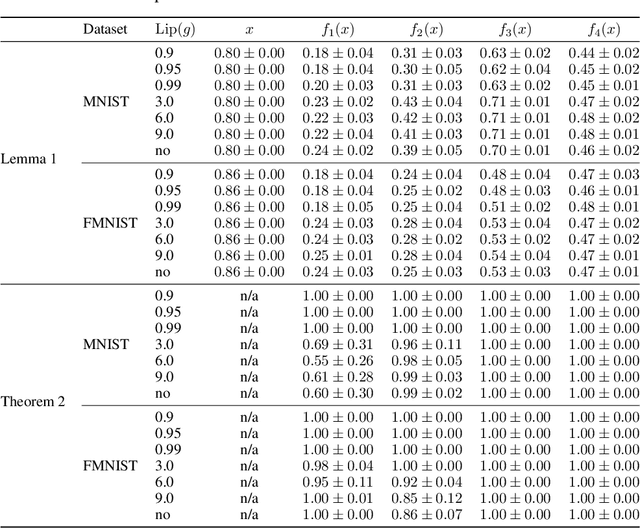
Abstract:ResNets constrained to be bi-Lipschitz, that is, approximately distance preserving, have been a crucial component of recently proposed techniques for deterministic uncertainty quantification in neural models. We show that theoretical justifications for recent regularisation schemes trying to enforce such a constraint suffer from a crucial flaw -- the theoretical link between the regularisation scheme used and bi-Lipschitzness is only valid under conditions which do not hold in practice, rendering existing theory of limited use, despite the strong empirical performance of these models. We provide a theoretical explanation for the effectiveness of these regularisation schemes using a frequency analysis perspective, showing that under mild conditions these schemes will enforce a lower Lipschitz bound on the low-frequency projection of images. We then provide empirical evidence supporting our theoretical claims, and perform further experiments which demonstrate that our broader conclusions appear to hold when some of the mathematical assumptions of our proof are relaxed, corresponding to the setup used in prior work. In addition, we present a simple constructive algorithm to search for counter examples to the distance preservation condition, and discuss possible implications of our theory for future model design.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge