SimuDICE: Offline Policy Optimization Through World Model Updates and DICE Estimation

In offline reinforcement learning, deriving an effective policy from a pre-collected set of experiences is challenging due to the distribution mismatch between the target policy and the behavioral policy used to collect the data, as well as the limited sample size. Model-based reinforcement learning improves sample efficiency by generating simulated experiences using a learned dynamic model of the environment. However, these synthetic experiences often suffer from the same distribution mismatch. To address these challenges, we introduce SimuDICE, a framework that iteratively refines the initial policy derived from offline data using synthetically generated experiences from the world model. SimuDICE enhances the quality of these simulated experiences by adjusting the sampling probabilities of state-action pairs based on stationary DIstribution Correction Estimation (DICE) and the estimated confidence in the model's predictions. This approach guides policy improvement by balancing experiences similar to those frequently encountered with ones that have a distribution mismatch. Our experiments show that SimuDICE achieves performance comparable to existing algorithms while requiring fewer pre-collected experiences and planning steps, and it remains robust across varying data collection policies.

When Do Off-Policy and On-Policy Policy Gradient Methods Align?

Policy gradient methods are widely adopted reinforcement learning algorithms for tasks with continuous action spaces. These methods succeeded in many application domains, however, because of their notorious sample inefficiency their use remains limited to problems where fast and accurate simulations are available. A common way to improve sample efficiency is to modify their objective function to be computable from off-policy samples without importance sampling. A well-established off-policy objective is the excursion objective. This work studies the difference between the excursion objective and the traditional on-policy objective, which we refer to as the on-off gap. We provide the first theoretical analysis showing conditions to reduce the on-off gap while establishing empirical evidence of shortfalls arising when these conditions are not met.

Domain Adaptation by Using Causal Inference to Predict Invariant Conditional Distributions

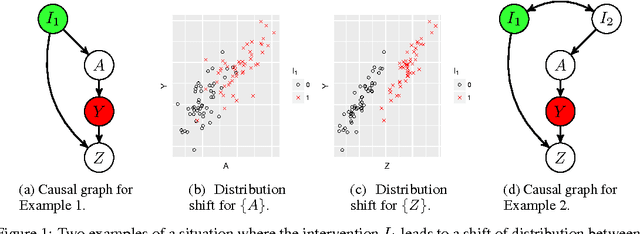
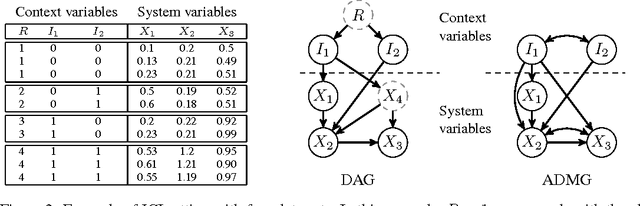
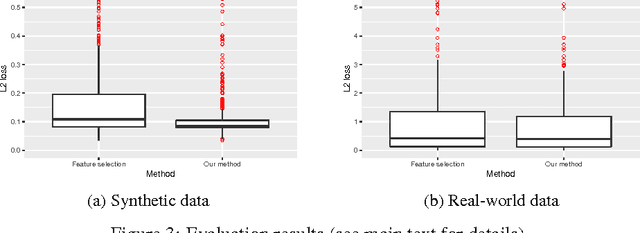
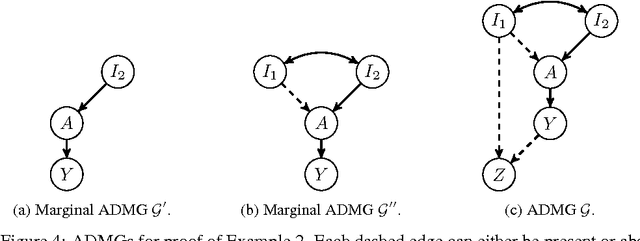
An important goal common to domain adaptation and causal inference is to make accurate predictions when the distributions for the source (or training) domain(s) and target (or test) domain(s) differ. In many cases, these different distributions can be modeled as different contexts of a single underlying system, in which each distribution corresponds to a different perturbation of the system, or in causal terms, an intervention. We focus on a class of such causal domain adaptation problems, where data for one or more source domains are given, and the task is to predict the distribution of a certain target variable from measurements of other variables in one or more target domains. We propose an approach for solving these problems that exploits causal inference and does not rely on prior knowledge of the causal graph, the type of interventions or the intervention targets. We demonstrate our approach by evaluating a possible implementation on simulated and real world data.

Theoretical Aspects of Cyclic Structural Causal Models

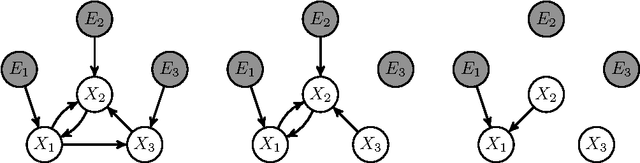
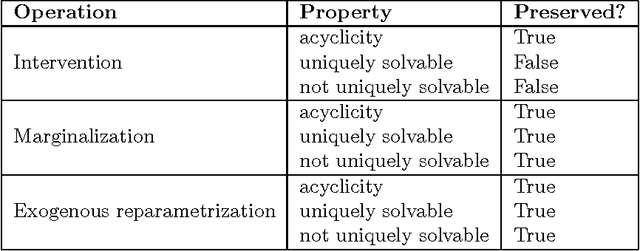
Structural causal models (SCMs), also known as (non-parametric) structural equation models (SEMs), are widely used for causal modeling purposes. A large body of theoretical results is available for the special case in which cycles are absent (i.e., acyclic SCMs, also known as recursive SEMs). However, in many application domains cycles are abundantly present, for example in the form of feedback loops. In this paper, we provide a general and rigorous theory of cyclic SCMs. The paper consists of two parts: the first part gives a rigorous treatment of structural causal models, dealing with measure-theoretic and other complications that arise in the presence of cycles. In contrast with the acyclic case, in cyclic SCMs solutions may no longer exist, or if they exist, they may no longer be unique, or even measurable in general. We give several sufficient and necessary conditions for the existence of (unique) measurable solutions. We show how causal reasoning proceeds in these models and how this differs from the acyclic case. Moreover, we give an overview of the Markov properties that hold for cyclic SCMs. In the second part, we address the question of how one can marginalize an SCM (possibly with cycles) to a subset of the endogenous variables. We show that under a certain condition, one can effectively remove a subset of the endogenous variables from the model, leading to a more parsimonious marginal SCM that preserves the causal and counterfactual semantics of the original SCM on the remaining variables. Moreover, we show how the marginalization relates to the latent projection and to latent confounders, i.e. latent common causes.

From Deterministic ODEs to Dynamic Structural Causal Models

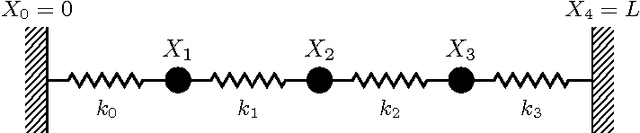
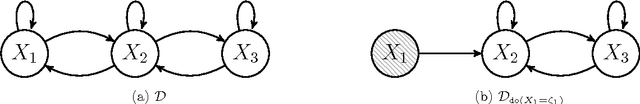
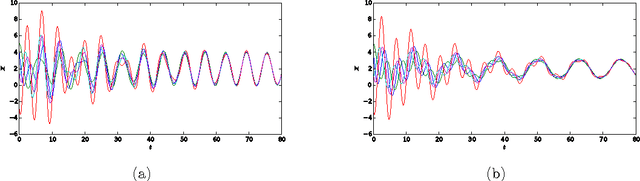
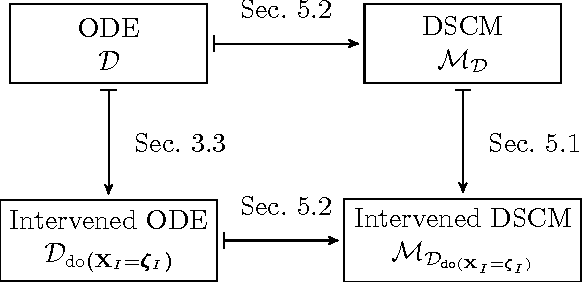
Structural Causal Models are widely used in causal modelling, but how they relate to other modelling tools is poorly understood. In this paper we provide a novel perspective on the relationship between Ordinary Differential Equations and Structural Causal Models. We show how, under certain conditions, the asymptotic behaviour of an Ordinary Differential Equation under non-constant interventions can be modelled using Dynamic Structural Causal Models. In contrast to earlier work, we study not only the effect of interventions on equilibrium states; rather, we model asymptotic behaviour that is dynamic under interventions that vary in time, and include as a special case the study of static equilibria.

From Random Differential Equations to Structural Causal Models: the stochastic case

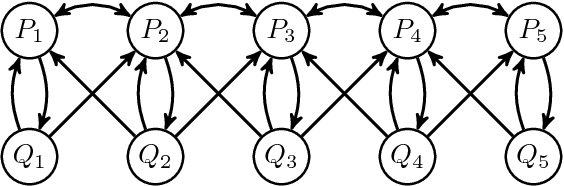
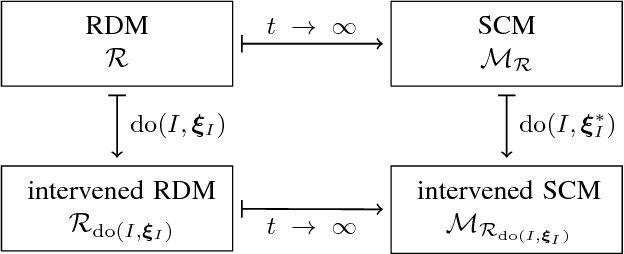
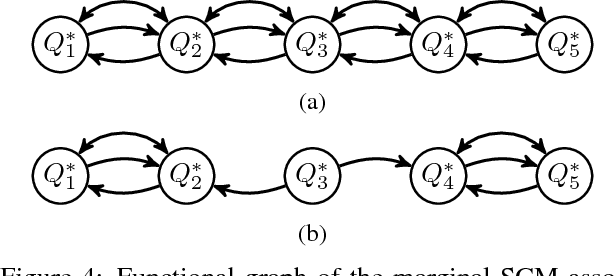
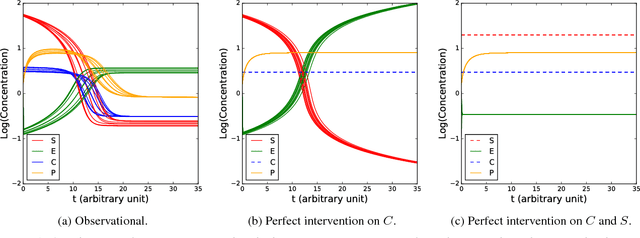
Random Differential Equations provide a natural extension of Ordinary Differential Equations to the stochastic setting. We show how, and under which conditions, every equilibrium state of a Random Differential Equation (RDE) can be described by a Structural Causal Model (SCM), while pertaining the causal semantics. This provides an SCM that captures the stochastic and causal behavior of the RDE, which can model both cycles and confounders. This enables the study of the equilibrium states of the RDE by applying the theory and statistical tools available for SCMs, for example, marginalizations and Markov properties, as we illustrate by means of an example. Our work thus provides a direct connection between two fields that so far have been developing in isolation.

Causal Consistency of Structural Equation Models

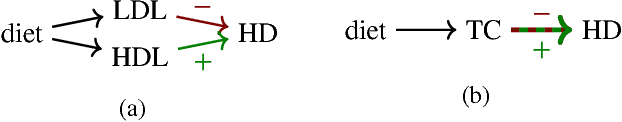
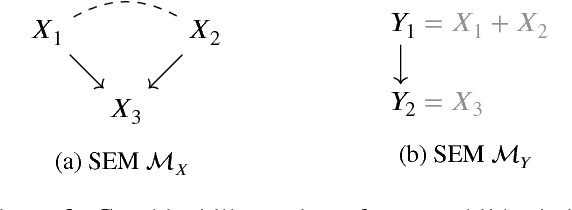
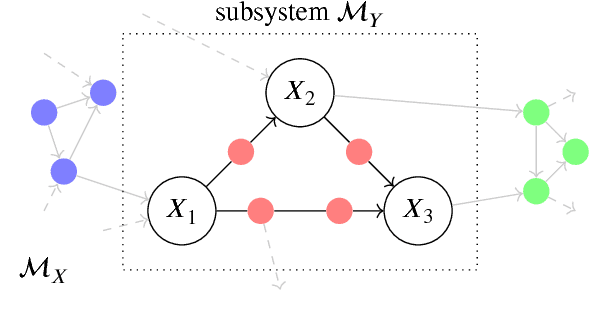
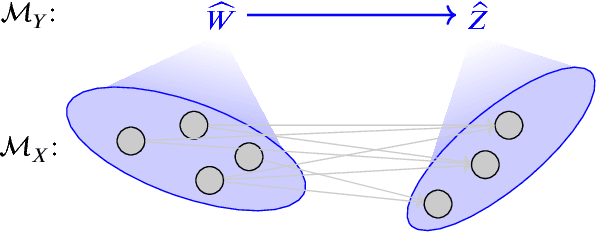
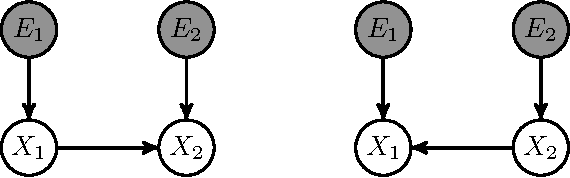
Complex systems can be modelled at various levels of detail. Ideally, causal models of the same system should be consistent with one another in the sense that they agree in their predictions of the effects of interventions. We formalise this notion of consistency in the case of Structural Equation Models (SEMs) by introducing exact transformations between SEMs. This provides a general language to consider, for instance, the different levels of description in the following three scenarios: (a) models with large numbers of variables versus models in which the `irrelevant' or unobservable variables have been marginalised out; (b) micro-level models versus macro-level models in which the macro-variables are aggregate features of the micro-variables; (c) dynamical time series models versus models of their stationary behaviour. Our analysis stresses the importance of well specified interventions in the causal modelling process and sheds light on the interpretation of cyclic SEMs.