Nonparametric Bayesian networks are typically faithful in the total variation metric

We show that for a given DAG $G$, among all observational distributions of Bayesian networks over $G$ with arbitrary outcome spaces, the faithful distributions are `typical': they constitute a dense, open set with respect to the total variation metric. As a consequence, the set of faithful distributions is non-empty, and the unfaithful distributions are nowhere dense. We extend this result to the space of Bayesian networks, where the properties hold for Bayesian networks instead of distributions of Bayesian networks. As special cases, we show that these results also hold for the faithful parameters of the subclasses of linear Gaussian -- and discrete Bayesian networks, giving a topological analogue of the measure-zero results of Spirtes et al. (1993) and Meek (1995). Finally, we extend our topological results and the measure-zero results of Spirtes et al. and Meek to Bayesian networks with latent variables.

Dynamic Structural Causal Models

We study a specific type of SCM, called a Dynamic Structural Causal Model (DSCM), whose endogenous variables represent functions of time, which is possibly cyclic and allows for latent confounding. As a motivating use-case, we show that certain systems of Stochastic Differential Equations (SDEs) can be appropriately represented with DSCMs. An immediate consequence of this construction is a graphical Markov property for systems of SDEs. We define a time-splitting operation, allowing us to analyse the concept of local independence (a notion of continuous-time Granger (non-)causality). We also define a subsampling operation, which returns a discrete-time DSCM, and which can be used for mathematical analysis of subsampled time-series. We give suggestions how DSCMs can be used for identification of the causal effect of time-dependent interventions, and how existing constraint-based causal discovery algorithms can be applied to time-series data.

Evaluating and Correcting Performative Effects of Decision Support Systems via Causal Domain Shift

When predicting a target variable $Y$ from features $X$, the prediction $\hat{Y}$ can be performative: an agent might act on this prediction, affecting the value of $Y$ that we eventually observe. Performative predictions are deliberately prevalent in algorithmic decision support, where a Decision Support System (DSS) provides a prediction for an agent to affect the value of the target variable. When deploying a DSS in high-stakes settings (e.g. healthcare, law, predictive policing, or child welfare screening) it is imperative to carefully assess the performative effects of the DSS. In the case that the DSS serves as an alarm for a predicted negative outcome, naive retraining of the prediction model is bound to result in a model that underestimates the risk, due to effective workings of the previous model. In this work, we propose to model the deployment of a DSS as causal domain shift and provide novel cross-domain identification results for the conditional expectation $E[Y | X]$, allowing for pre- and post-hoc assessment of the deployment of the DSS, and for retraining of a model that assesses the risk under a baseline policy where the DSS is not deployed. Using a running example, we empirically show that a repeated regression procedure provides a practical framework for estimating these quantities, even when the data is affected by sample selection bias and selective labelling, offering for a practical, unified solution for multiple forms of target variable bias.

Modeling Latent Selection with Structural Causal Models

Selection bias is ubiquitous in real-world data, and can lead to misleading results if not dealt with properly. We introduce a conditioning operation on Structural Causal Models (SCMs) to model latent selection from a causal perspective. We show that the conditioning operation transforms an SCM with the presence of an explicit latent selection mechanism into an SCM without such selection mechanism, which partially encodes the causal semantics of the selected subpopulation according to the original SCM. Furthermore, we show that this conditioning operation preserves the simplicity, acyclicity, and linearity of SCMs, and commutes with marginalization. Thanks to these properties, combined with marginalization and intervention, the conditioning operation offers a valuable tool for conducting causal reasoning tasks within causal models where latent details have been abstracted away. We demonstrate by example how classical results of causal inference can be generalized to include selection bias and how the conditioning operation helps with modeling of real-world problems.

Establishing Markov Equivalence in Cyclic Directed Graphs

We present a new, efficient procedure to establish Markov equivalence between directed graphs that may or may not contain cycles under the \textit{d}-separation criterion. It is based on the Cyclic Equivalence Theorem (CET) in the seminal works on cyclic models by Thomas Richardson in the mid '90s, but now rephrased from an ancestral perspective. The resulting characterization leads to a procedure for establishing Markov equivalence between graphs that no longer requires tests for d-separation, leading to a significantly reduced algorithmic complexity. The conceptually simplified characterization may help to reinvigorate theoretical research towards sound and complete cyclic discovery in the presence of latent confounders. This version includes a correction to rule (iv) in Theorem 1, and the subsequent adjustment in part 2 of Algorithm 2.

Correcting for Selection Bias and Missing Response in Regression using Privileged Information

When estimating a regression model, we might have data where some labels are missing, or our data might be biased by a selection mechanism. When the response or selection mechanism is ignorable (i.e., independent of the response variable given the features) one can use off-the-shelf regression methods; in the nonignorable case one typically has to adjust for bias. We observe that privileged data (i.e. data that is only available during training) might render a nonignorable selection mechanism ignorable, and we refer to this scenario as Privilegedly Missing at Random (PMAR). We propose a novel imputation-based regression method, named repeated regression, that is suitable for PMAR. We also consider an importance weighted regression method, and a doubly robust combination of the two. The proposed methods are easy to implement with most popular out-of-the-box regression algorithms. We empirically assess the performance of the proposed methods with extensive simulated experiments and on a synthetically augmented real-world dataset. We conclude that repeated regression can appropriately correct for bias, and can have considerable advantage over weighted regression, especially when extrapolating to regions of the feature space where response is never observed.

Local Constraint-Based Causal Discovery under Selection Bias

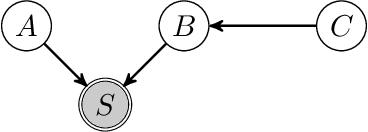
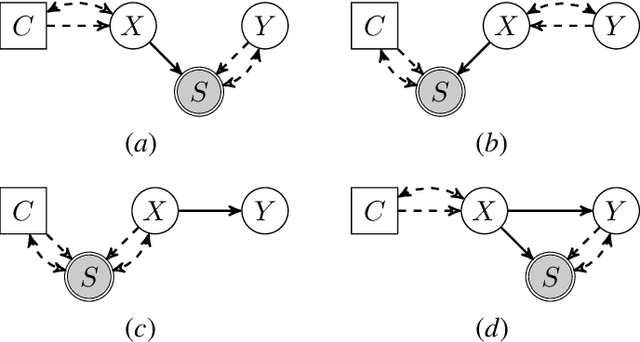
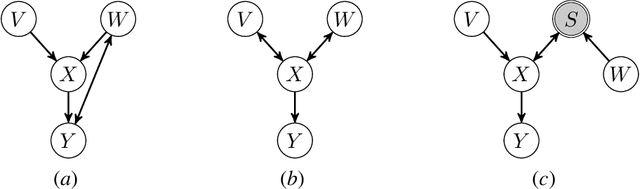
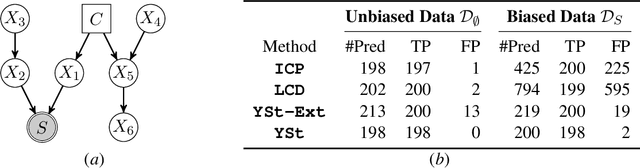
We consider the problem of discovering causal relations from independence constraints selection bias in addition to confounding is present. While the seminal FCI algorithm is sound and complete in this setup, no criterion for the causal interpretation of its output under selection bias is presently known. We focus instead on local patterns of independence relations, where we find no sound method for only three variable that can include background knowledge. Y-Structure patterns are shown to be sound in predicting causal relations from data under selection bias, where cycles may be present. We introduce a finite-sample scoring rule for Y-Structures that is shown to successfully predict causal relations in simulation experiments that include selection mechanisms. On real-world microarray data, we show that a Y-Structure variant performs well across different datasets, potentially circumventing spurious correlations due to selection bias.

Efficient Causal Inference from Combined Observational and Interventional Data through Causal Reductions

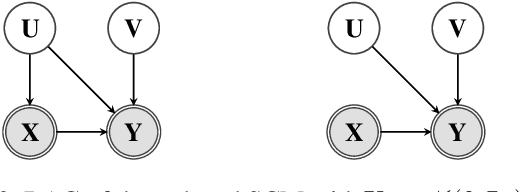
Unobserved confounding is one of the main challenges when estimating causal effects. We propose a novel causal reduction method that replaces an arbitrary number of possibly high-dimensional latent confounders with a single latent confounder that lives in the same space as the treatment variable without changing the observational and interventional distributions entailed by the causal model. After the reduction, we parameterize the reduced causal model using a flexible class of transformations, so-called normalizing flows. We propose a learning algorithm to estimate the parameterized reduced model jointly from observational and interventional data. This allows us to estimate the causal effect in a principled way from combined data. We perform a series of experiments on data simulated using nonlinear causal mechanisms and find that we can often substantially reduce the number of interventional samples when adding observational training samples without sacrificing accuracy. Thus, adding observational data may help to more accurately estimate causal effects even in the presence of unobserved confounders.

Causality and independence in perfectly adapted dynamical systems

Perfect adaptation in a dynamical system is the phenomenon that one or more variables have an initial transient response to a persistent change in an external stimulus but revert to their original value as the system converges to equilibrium. The causal ordering algorithm can be used to construct an equilibrium causal ordering graph that represents causal relations and a Markov ordering graph that implies conditional independences from a set of equilibrium equations. Based on this, we formulate sufficient graphical conditions to identify perfect adaptation from a set of first-order differential equations. Furthermore, we give sufficient conditions to test for the presence of perfect adaptation in experimental equilibrium data. We apply our ideas to a simple model for a protein signalling pathway and test its predictions both in simulations and on real-world protein expression data. We demonstrate that perfect adaptation in this model can explain why the presence and orientation of edges in the output of causal discovery algorithms does not always appear to agree with the direction of edges in biological consensus networks.

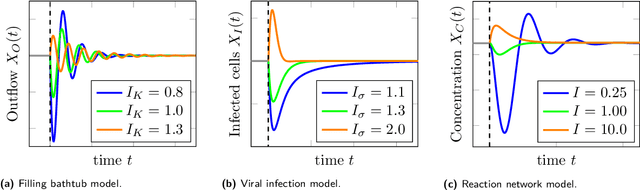
Robustness of Model Predictions under Extension

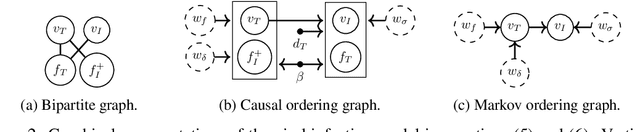
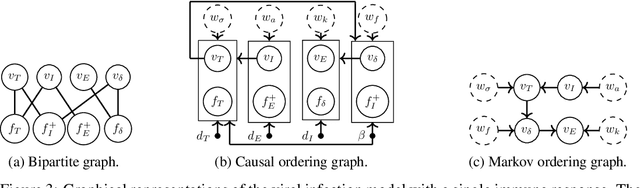
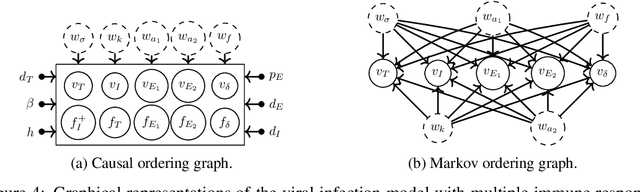
Often, mathematical models of the real world are simplified representations of complex systems. A caveat to using models for analysis is that predicted causal effects and conditional independences may not be robust under model extensions, and therefore applicability of such models is limited. In this work, we consider conditions under which qualitative model predictions are preserved when two models are combined. We show how to use the technique of causal ordering to efficiently assess the robustness of qualitative model predictions and characterize a large class of model extensions that preserve these predictions. For dynamical systems at equilibrium, we demonstrate how novel insights help to select appropriate model extensions and to reason about the presence of feedback loops. We apply our ideas to a viral infection model with immune responses.