Shuzhong Zhang
A Unified Analysis for the Subgradient Methods Minimizing Composite Nonconvex, Nonsmooth and Non-Lipschitz Functions
Aug 30, 2023Abstract:In this paper we propose a proximal subgradient method (Prox-SubGrad) for solving nonconvex and nonsmooth optimization problems without assuming Lipschitz continuity conditions. A number of subgradient upper bounds and their relationships are presented. By means of these upper bounding conditions, we establish some uniform recursive relations for the Moreau envelopes for weakly convex optimization. This uniform scheme simplifies and unifies the proof schemes to establish rate of convergence for Prox-SubGrad without assuming Lipschitz continuity. We present a novel convergence analysis in this context. Furthermore, we propose some new stochastic subgradient upper bounding conditions and establish convergence and iteration complexity rates for the stochastic subgradient method (Sto-SubGrad) to solve non-Lipschitz and nonsmooth stochastic optimization problems. In particular, for both deterministic and stochastic subgradient methods on weakly convex optimization problems without Lipschitz continuity, under any of the subgradient upper bounding conditions to be introduced in the paper, we show that $O(1/\sqrt{T})$ convergence rate holds in terms of the square of gradient of the Moreau envelope function, which further improves to be $O(1/{T})$ if, in addition, the uniform KL condition with exponent $1/2$ holds.
An Augmented Lagrangian Approach to Conically Constrained Non-monotone Variational Inequality Problems
Jun 02, 2023Abstract:In this paper we consider a non-monotone (mixed) variational inequality model with (nonlinear) convex conic constraints. Through developing an equivalent Lagrangian function-like primal-dual saddle-point system for the VI model in question, we introduce an augmented Lagrangian primal-dual method, to be called ALAVI in the current paper, for solving a general constrained VI model. Under an assumption, to be called the primal-dual variational coherence condition in the paper, we prove the convergence of ALAVI. Next, we show that many existing generalized monotonicity properties are sufficient -- though by no means necessary -- to imply the above mentioned coherence condition, thus are sufficient to ensure convergence of ALAVI. Under that assumption, we further show that ALAVI has in fact an $o(1/\sqrt{k})$ global rate of convergence where $k$ is the iteration count. By introducing a new gap function, this rate further improves to be $O(1/k)$ if the mapping is monotone. Finally, we show that under a metric subregularity condition, even if the VI model may be non-monotone the local convergence rate of ALAVI improves to be linear. Numerical experiments on some randomly generated highly nonlinear and non-monotone VI problems show practical efficacy of the newly proposed method.
Cubic-Regularized Newton for Spectral Constrained Matrix Optimization and its Application to Fairness
Sep 02, 2022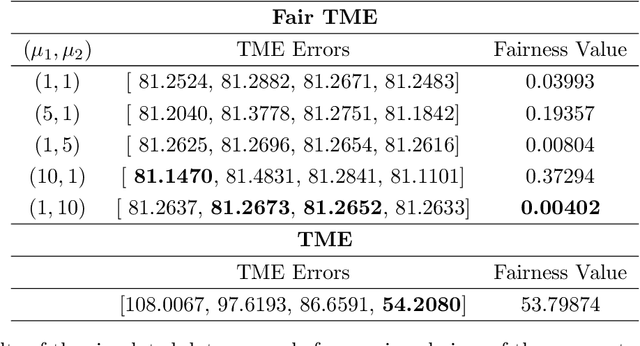
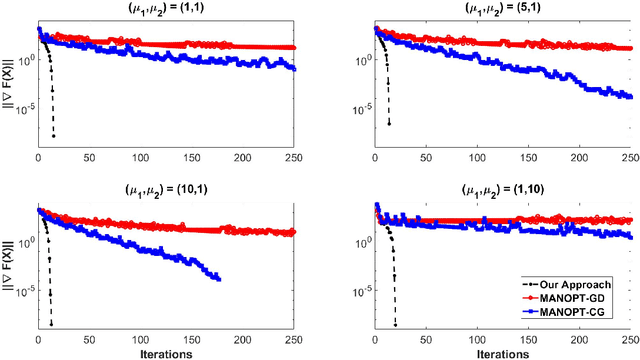
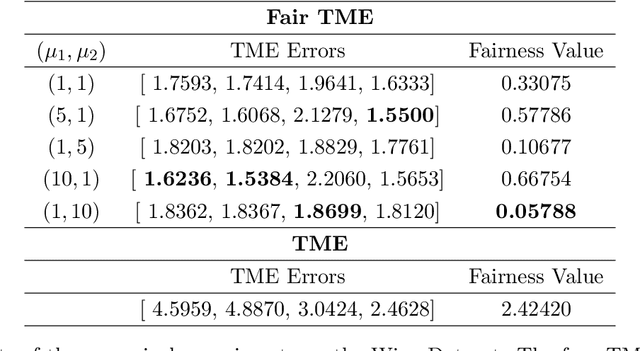
Abstract:Matrix functions are utilized to rewrite smooth spectral constrained matrix optimization problems as smooth unconstrained problems over the set of symmetric matrices which are then solved via the cubic-regularized Newton method. A second-order chain rule identity for matrix functions is proven to compute the higher-order derivatives to implement cubic-regularized Newton, and a new convergence analysis is provided for cubic-regularized Newton for matrix vector spaces. We demonstrate the applicability of our approach by conducting numerical experiments on both synthetic and real datasets. In our experiments, we formulate a new model for estimating fair and robust covariance matrices in the spirit of the Tyler's M-estimator (TME) model and demonstrate its advantage.
Binary Random Projections with Controllable Sparsity Patterns
Jun 29, 2020


Abstract:Random projection is often used to project higher-dimensional vectors onto a lower-dimensional space, while approximately preserving their pairwise distances. It has emerged as a powerful tool in various data processing tasks and has attracted considerable research interest. Partly motivated by the recent discoveries in neuroscience, in this paper we study the problem of random projection using binary matrices with controllable sparsity patterns. Specifically, we proposed two sparse binary projection models that work on general data vectors. Compared with the conventional random projection models with dense projection matrices, our proposed models enjoy significant computational advantages due to their sparsity structure, as well as improved accuracies in empirical evaluations.
Highly accurate model for prediction of lung nodule malignancy with CT scans
Feb 06, 2018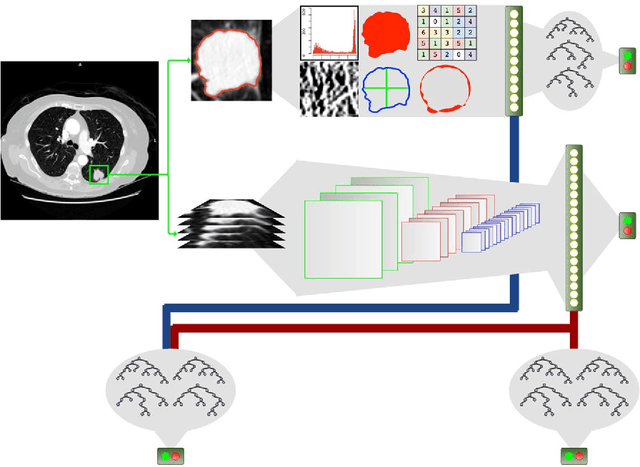
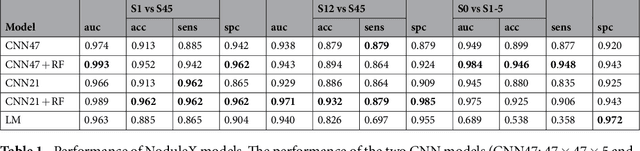
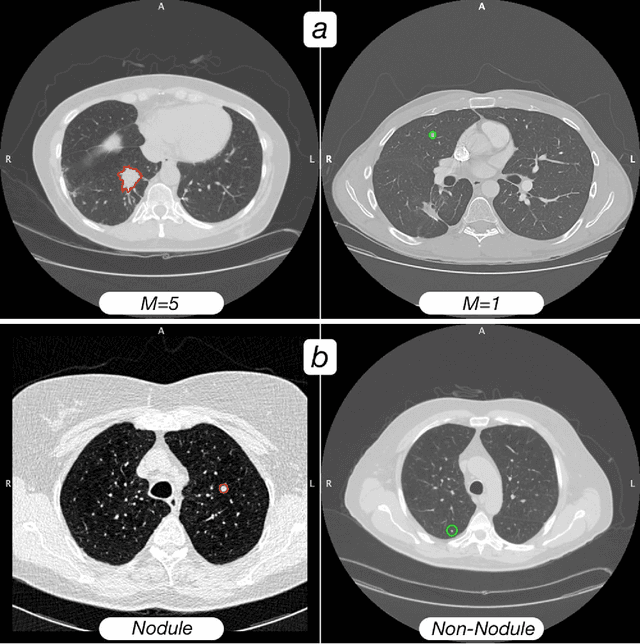
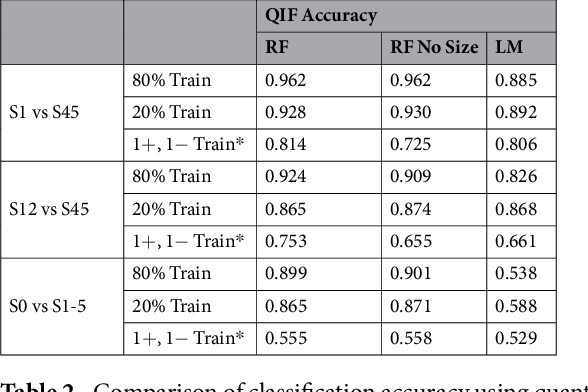
Abstract:Computed tomography (CT) examinations are commonly used to predict lung nodule malignancy in patients, which are shown to improve noninvasive early diagnosis of lung cancer. It remains challenging for computational approaches to achieve performance comparable to experienced radiologists. Here we present NoduleX, a systematic approach to predict lung nodule malignancy from CT data, based on deep learning convolutional neural networks (CNN). For training and validation, we analyze >1000 lung nodules in images from the LIDC/IDRI cohort. All nodules were identified and classified by four experienced thoracic radiologists who participated in the LIDC project. NoduleX achieves high accuracy for nodule malignancy classification, with an AUC of ~0.99. This is commensurate with the analysis of the dataset by experienced radiologists. Our approach, NoduleX, provides an effective framework for highly accurate nodule malignancy prediction with the model trained on a large patient population. Our results are replicable with software available at http://bioinformatics.astate.edu/NoduleX.
Structured Nonconvex and Nonsmooth Optimization: Algorithms and Iteration Complexity Analysis
Jan 17, 2018

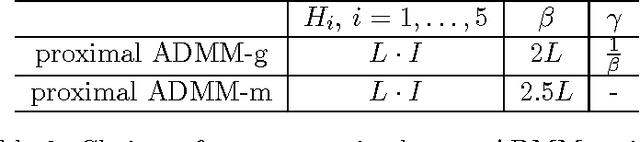
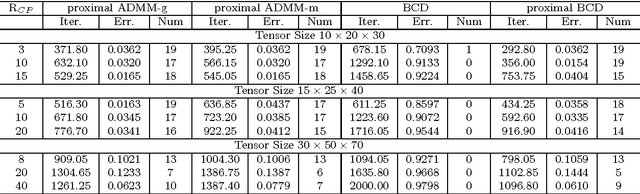
Abstract:Nonconvex and nonsmooth optimization problems are frequently encountered in much of statistics, business, science and engineering, but they are not yet widely recognized as a technology in the sense of scalability. A reason for this relatively low degree of popularity is the lack of a well developed system of theory and algorithms to support the applications, as is the case for its convex counterpart. This paper aims to take one step in the direction of disciplined nonconvex and nonsmooth optimization. In particular, we consider in this paper some constrained nonconvex optimization models in block decision variables, with or without coupled affine constraints. In the case of without coupled constraints, we show a sublinear rate of convergence to an $\epsilon$-stationary solution in the form of variational inequality for a generalized conditional gradient method, where the convergence rate is shown to be dependent on the H\"olderian continuity of the gradient of the smooth part of the objective. For the model with coupled affine constraints, we introduce corresponding $\epsilon$-stationarity conditions, and apply two proximal-type variants of the ADMM to solve such a model, assuming the proximal ADMM updates can be implemented for all the block variables except for the last block, for which either a gradient step or a majorization-minimization step is implemented. We show an iteration complexity bound of $O(1/\epsilon^2)$ to reach an $\epsilon$-stationary solution for both algorithms. Moreover, we show that the same iteration complexity of a proximal BCD method follows immediately. Numerical results are provided to illustrate the efficacy of the proposed algorithms for tensor robust PCA.
Global Convergence of Unmodified 3-Block ADMM for a Class of Convex Minimization Problems
Jan 17, 2018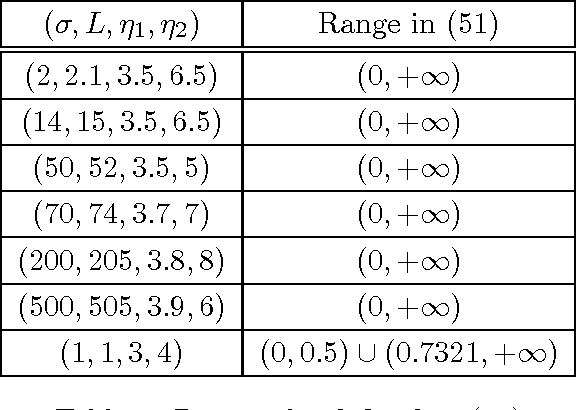
Abstract:The alternating direction method of multipliers (ADMM) has been successfully applied to solve structured convex optimization problems due to its superior practical performance. The convergence properties of the 2-block ADMM have been studied extensively in the literature. Specifically, it has been proven that the 2-block ADMM globally converges for any penalty parameter $\gamma>0$. In this sense, the 2-block ADMM allows the parameter to be free, i.e., there is no need to restrict the value for the parameter when implementing this algorithm in order to ensure convergence. However, for the 3-block ADMM, Chen \etal \cite{Chen-admm-failure-2013} recently constructed a counter-example showing that it can diverge if no further condition is imposed. The existing results on studying further sufficient conditions on guaranteeing the convergence of the 3-block ADMM usually require $\gamma$ to be smaller than a certain bound, which is usually either difficult to compute or too small to make it a practical algorithm. In this paper, we show that the 3-block ADMM still globally converges with any penalty parameter $\gamma>0$ if the third function $f_3$ in the objective is smooth and strongly convex, and its condition number is in $[1,1.0798)$, besides some other mild conditions. This requirement covers an important class of problems to be called regularized least squares decomposition (RLSD) in this paper.
Accelerated Primal-Dual Proximal Block Coordinate Updating Methods for Constrained Convex Optimization
Nov 20, 2017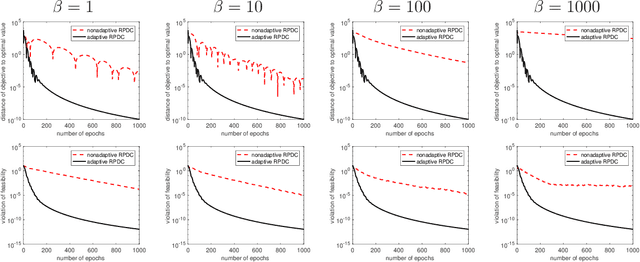

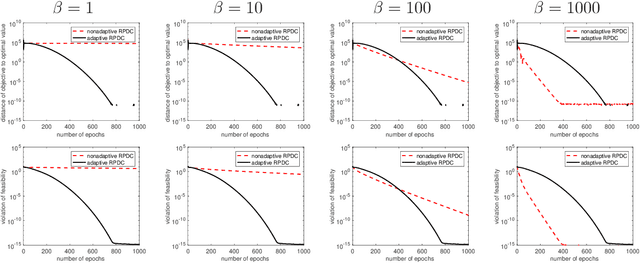

Abstract:Block Coordinate Update (BCU) methods enjoy low per-update computational complexity because every time only one or a few block variables would need to be updated among possibly a large number of blocks. They are also easily parallelized and thus have been particularly popular for solving problems involving large-scale dataset and/or variables. In this paper, we propose a primal-dual BCU method for solving linearly constrained convex program in multi-block variables. The method is an accelerated version of a primal-dual algorithm proposed by the authors, which applies randomization in selecting block variables to update and establishes an $O(1/t)$ convergence rate under weak convexity assumption. We show that the rate can be accelerated to $O(1/t^2)$ if the objective is strongly convex. In addition, if one block variable is independent of the others in the objective, we then show that the algorithm can be modified to achieve a linear rate of convergence. The numerical experiments show that the accelerated method performs stably with a single set of parameters while the original method needs to tune the parameters for different datasets in order to achieve a comparable level of performance.
Primal-Dual Optimization Algorithms over Riemannian Manifolds: an Iteration Complexity Analysis
Oct 05, 2017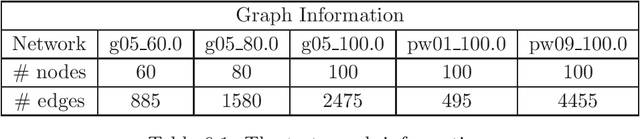
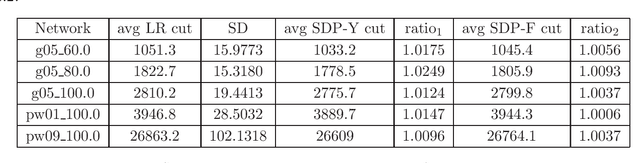
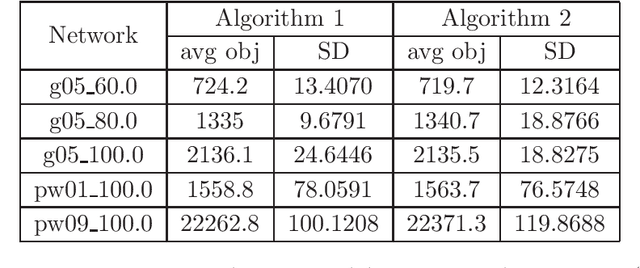

Abstract:In this paper we study nonconvex and nonsmooth multi-block optimization over Riemannian manifolds with coupled linear constraints. Such optimization problems naturally arise from machine learning, statistical learning, compressive sensing, image processing, and tensor PCA, among others. We develop an ADMM-like primal-dual approach based on decoupled solvable subroutines such as linearized proximal mappings. First, we introduce the optimality conditions for the afore-mentioned optimization models. Then, the notion of $\epsilon$-stationary solutions is introduced as a result. The main part of the paper is to show that the proposed algorithms enjoy an iteration complexity of $O(1/\epsilon^2)$ to reach an $\epsilon$-stationary solution. For prohibitively large-size tensor or machine learning models, we present a sampling-based stochastic algorithm with the same iteration complexity bound in expectation. In case the subproblems are not analytically solvable, a feasible curvilinear line-search variant of the algorithm based on retraction operators is proposed. Finally, we show specifically how the algorithms can be implemented to solve a variety of practical problems such as the NP-hard maximum bisection problem, the $\ell_q$ regularized sparse tensor principal component analysis and the community detection problem. Our preliminary numerical results show great potentials of the proposed methods.
Randomized Primal-Dual Proximal Block Coordinate Updates
Jan 24, 2017Abstract:In this paper we propose a randomized primal-dual proximal block coordinate updating framework for a general multi-block convex optimization model with coupled objective function and linear constraints. Assuming mere convexity, we establish its $O(1/t)$ convergence rate in terms of the objective value and feasibility measure. The framework includes several existing algorithms as special cases such as a primal-dual method for bilinear saddle-point problems (PD-S), the proximal Jacobian ADMM (Prox-JADMM) and a randomized variant of the ADMM method for multi-block convex optimization. Our analysis recovers and/or strengthens the convergence properties of several existing algorithms. For example, for PD-S our result leads to the same order of convergence rate without the previously assumed boundedness condition on the constraint sets, and for Prox-JADMM the new result provides convergence rate in terms of the objective value and the feasibility violation. It is well known that the original ADMM may fail to converge when the number of blocks exceeds two. Our result shows that if an appropriate randomization procedure is invoked to select the updating blocks, then a sublinear rate of convergence in expectation can be guaranteed for multi-block ADMM, without assuming any strong convexity. The new approach is also extended to solve problems where only a stochastic approximation of the (sub-)gradient of the objective is available, and we establish an $O(1/\sqrt{t})$ convergence rate of the extended approach for solving stochastic programming.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge