Hölder Bounds for Sensitivity Analysis in Causal Reasoning

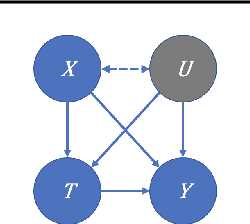
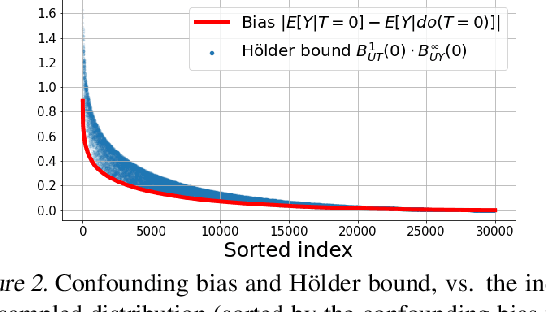
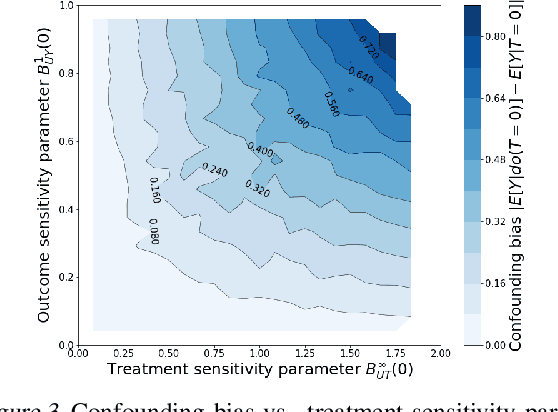
We examine interval estimation of the effect of a treatment T on an outcome Y given the existence of an unobserved confounder U. Using H\"older's inequality, we derive a set of bounds on the confounding bias |E[Y|T=t]-E[Y|do(T=t)]| based on the degree of unmeasured confounding (i.e., the strength of the connection U->T, and the strength of U->Y). These bounds are tight either when U is independent of T or when U is independent of Y given T (when there is no unobserved confounding). We focus on a special case of this bound depending on the total variation distance between the distributions p(U) and p(U|T=t), as well as the maximum (over all possible values of U) deviation of the conditional expected outcome E[Y|U=u,T=t] from the average expected outcome E[Y|T=t]. We discuss possible calibration strategies for this bound to get interval estimates for treatment effects, and experimentally validate the bound using synthetic and semi-synthetic datasets.

Counterfactual Representation Learning with Balancing Weights

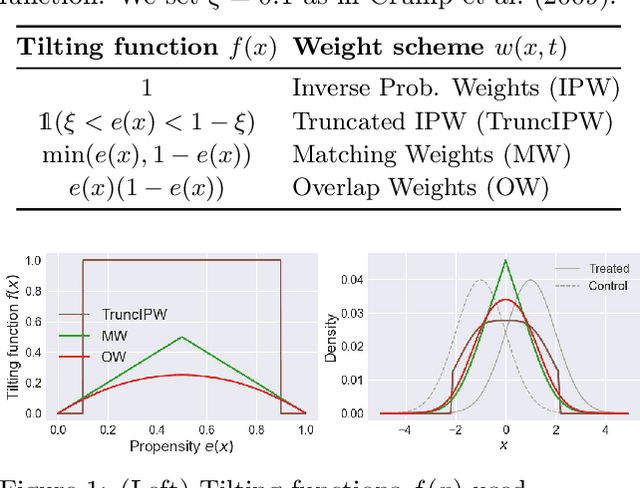
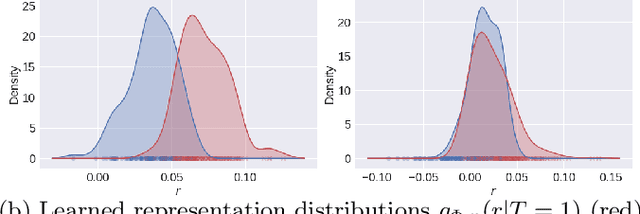
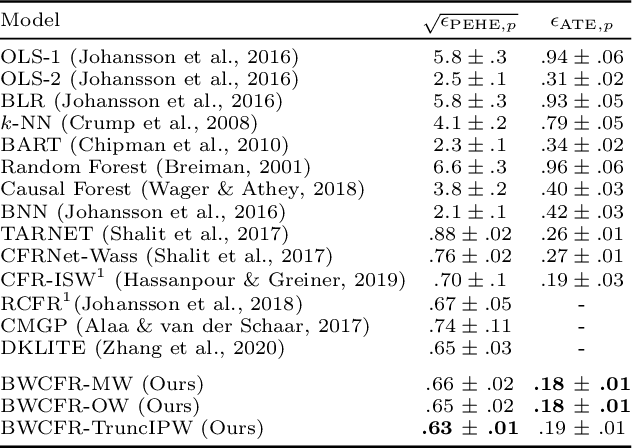
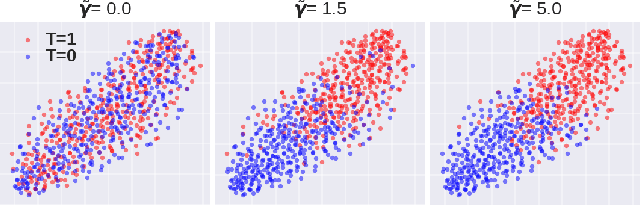
A key to causal inference with observational data is achieving balance in predictive features associated with each treatment type. Recent literature has explored representation learning to achieve this goal. In this work, we discuss the pitfalls of these strategies - such as a steep trade-off between achieving balance and predictive power - and present a remedy via the integration of balancing weights in causal learning. Specifically, we theoretically link balance to the quality of propensity estimation, emphasize the importance of identifying a proper target population, and elaborate on the complementary roles of feature balancing and weight adjustments. Using these concepts, we then develop an algorithm for flexible, scalable and accurate estimation of causal effects. Finally, we show how the learned weighted representations may serve to facilitate alternative causal learning procedures with appealing statistical features. We conduct an extensive set of experiments on both synthetic examples and standard benchmarks, and report encouraging results relative to state-of-the-art baselines.

Causal Transfer Random Forest: Combining Logged Data and Randomized Experiments for Robust Prediction

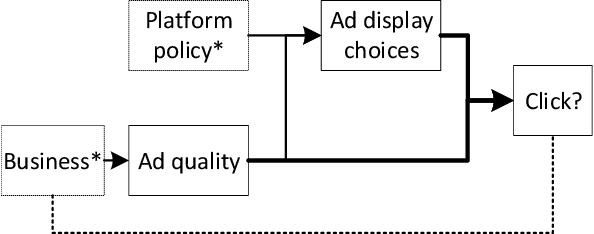
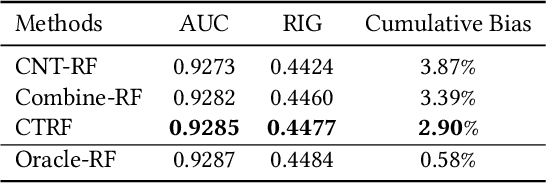
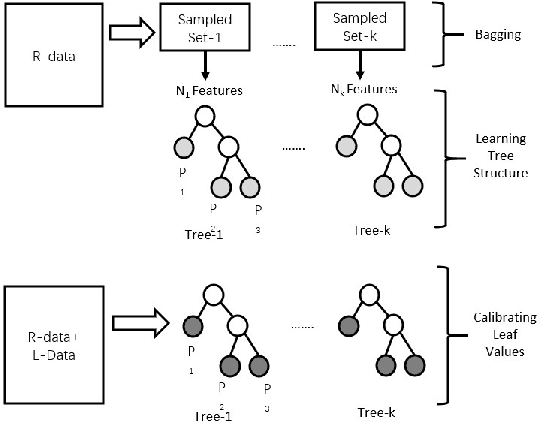
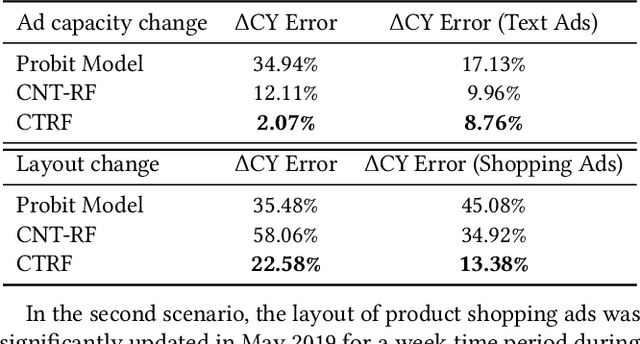
It is often critical for prediction models to be robust to distributional shifts between training and testing data. Viewed from a causal perspective, the challenge is to distinguish the stable causal relationships from the unstable spurious correlations across shifts. We describe a causal transfer random forest (CTRF) that combines existing training data with a small amount of data from a randomized experiment to train a model which is robust to the feature shifts and therefore transfers to a new targeting distribution. Theoretically, we justify the robustness of the approach against feature shifts with the knowledge from causal learning. Empirically, we evaluate the CTRF using both synthetic data experiments and real-world experiments in the Bing Ads platform, including a click prediction task and in the context of an end-to-end counterfactual optimization system. The proposed CTRF produces robust predictions and outperforms most baseline methods compared in the presence of feature shifts.

Double Robust Representation Learning for Counterfactual Prediction

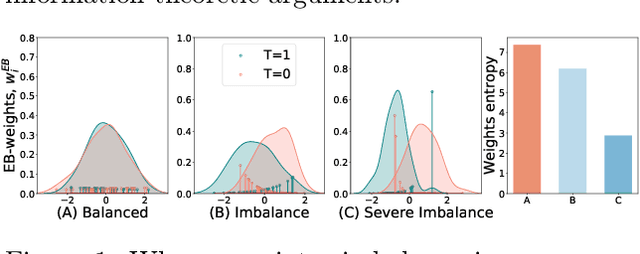
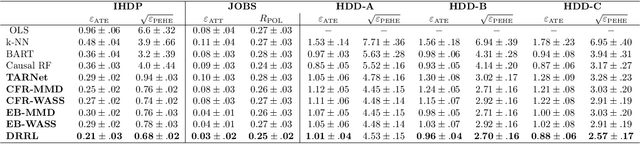
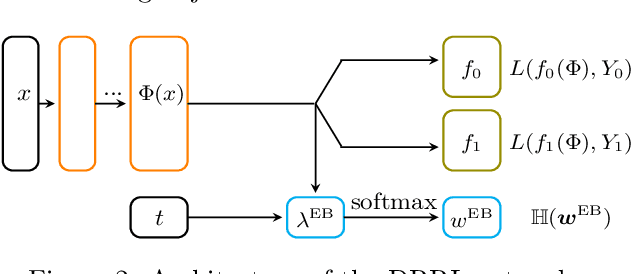
Causal inference, or counterfactual prediction, is central to decision making in healthcare, policy and social sciences. To de-bias causal estimators with high-dimensional data in observational studies, recent advances suggest the importance of combining machine learning models for both the propensity score and the outcome function. We propose a novel scalable method to learn double-robust representations for counterfactual predictions, leading to consistent causal estimation if the model for either the propensity score or the outcome, but not necessarily both, is correctly specified. Specifically, we use the entropy balancing method to learn the weights that minimize the Jensen-Shannon divergence of the representation between the treated and control groups, based on which we make robust and efficient counterfactual predictions for both individual and average treatment effects. We provide theoretical justifications for the proposed method. The algorithm shows competitive performance with the state-of-the-art on real world and synthetic data.

Survival Analysis meets Counterfactual Inference

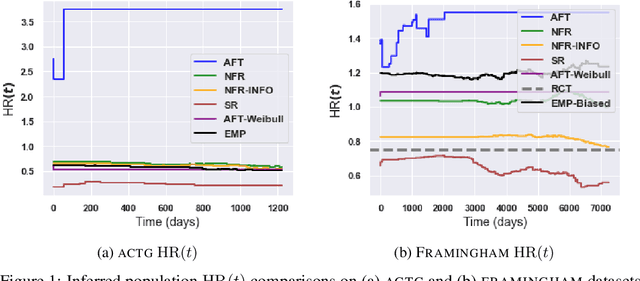
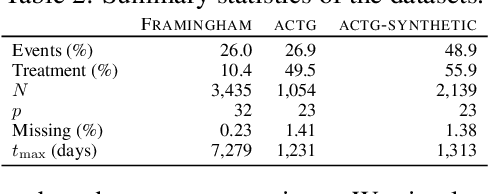
There is growing interest in applying machine learning methods for counterfactual inference from observational data. However, approaches that account for survival outcomes are relatively limited. Survival data are frequently encountered across diverse medical applications, \textit{i.e.}, drug development, risk profiling, and clinical trials, and such data are also relevant in fields like manufacturing (for equipment monitoring). When the outcome of interest is time-to-event, special precautions for handling censored events need to be taken, as ignoring censored outcomes may lead to biased estimates. We propose a theoretically grounded unified framework for counterfactual inference applicable to survival outcomes. Further, we formulate a nonparametric hazard ratio metric for evaluating average and individualized treatment effects. Experimental results on real-world and semi-synthetic datasets, the latter which we introduce, demonstrate that the proposed approach significantly outperforms competitive alternatives in both survival-outcome predictions and treatment-effect estimation.