Henry Pfister
Hölder Bounds for Sensitivity Analysis in Causal Reasoning
Jul 09, 2021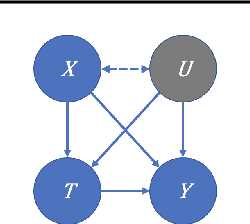

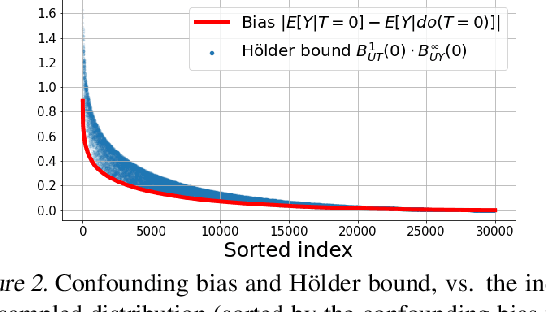
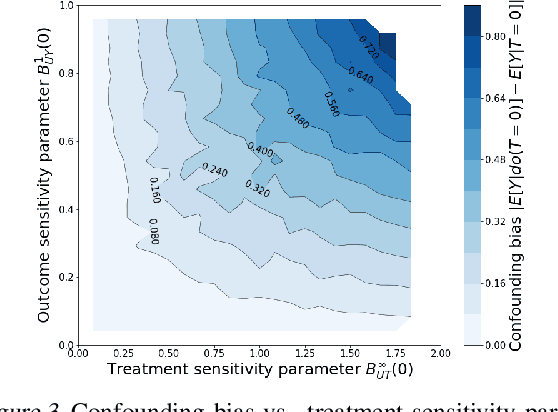
Abstract:We examine interval estimation of the effect of a treatment T on an outcome Y given the existence of an unobserved confounder U. Using H\"older's inequality, we derive a set of bounds on the confounding bias |E[Y|T=t]-E[Y|do(T=t)]| based on the degree of unmeasured confounding (i.e., the strength of the connection U->T, and the strength of U->Y). These bounds are tight either when U is independent of T or when U is independent of Y given T (when there is no unobserved confounding). We focus on a special case of this bound depending on the total variation distance between the distributions p(U) and p(U|T=t), as well as the maximum (over all possible values of U) deviation of the conditional expected outcome E[Y|U=u,T=t] from the average expected outcome E[Y|T=t]. We discuss possible calibration strategies for this bound to get interval estimates for treatment effects, and experimentally validate the bound using synthetic and semi-synthetic datasets.
Adversarial Defense of Image Classification Using a Variational Auto-Encoder
Dec 07, 2018
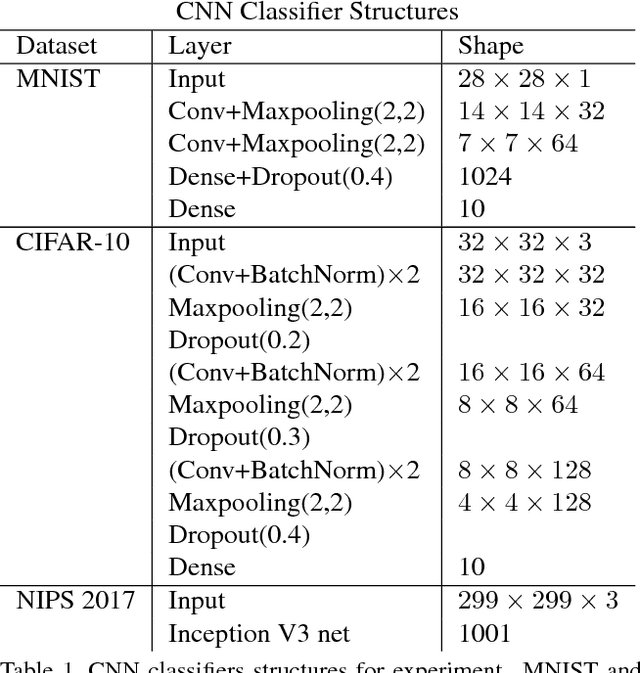
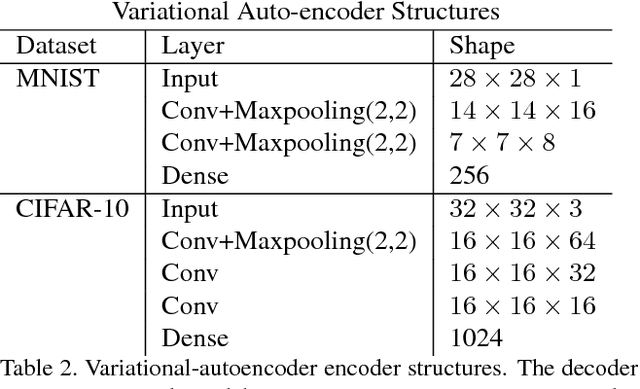
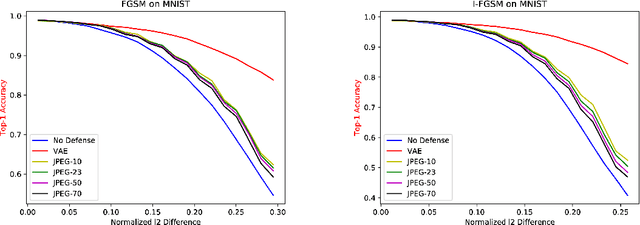
Abstract:Deep neural networks are known to be vulnerable to adversarial attacks. This exposes them to potential exploits in security-sensitive applications and highlights their lack of robustness. This paper uses a variational auto-encoder (VAE) to defend against adversarial attacks for image classification tasks. This VAE defense has a few nice properties: (1) it is quite flexible and its use of randomness makes it harder to attack; (2) it can learn disentangled representations that prevent blurry reconstruction; and (3) a patch-wise VAE defense strategy is used that does not require retraining for different size images. For moderate to severe attacks, this system outperforms or closely matches the performance of JPEG compression, with the best quality parameter. It also has more flexibility and potential for improvement via training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge