Neural Network Training with Asymmetric Crosspoint Elements

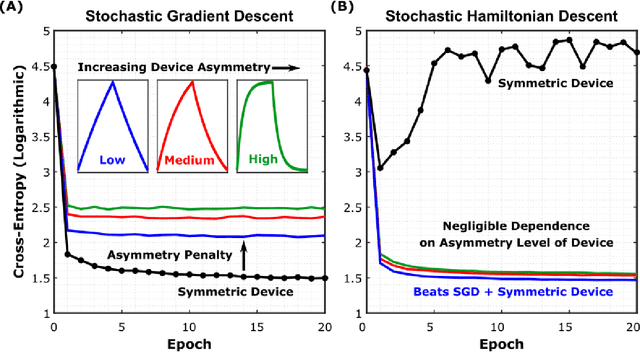
Analog crossbar arrays comprising programmable nonvolatile resistors are under intense investigation for acceleration of deep neural network training. However, the ubiquitous asymmetric conductance modulation of practical resistive devices critically degrades the classification performance of networks trained with conventional algorithms. Here, we describe and experimentally demonstrate an alternative fully-parallel training algorithm: Stochastic Hamiltonian Descent. Instead of conventionally tuning weights in the direction of the error function gradient, this method programs the network parameters to successfully minimize the total energy (Hamiltonian) of the system that incorporates the effects of device asymmetry. We provide critical intuition on why device asymmetry is fundamentally incompatible with conventional training algorithms and how the new approach exploits it as a useful feature instead. Our technique enables immediate realization of analog deep learning accelerators based on readily available device technologies.

EiGLasso for Scalable Sparse Kronecker-Sum Inverse Covariance Estimation

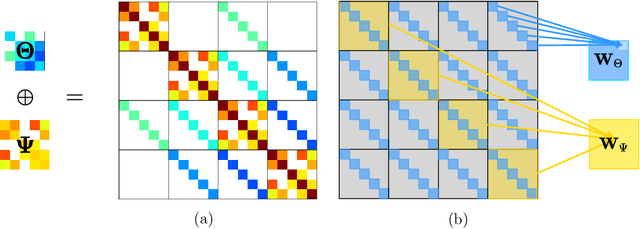
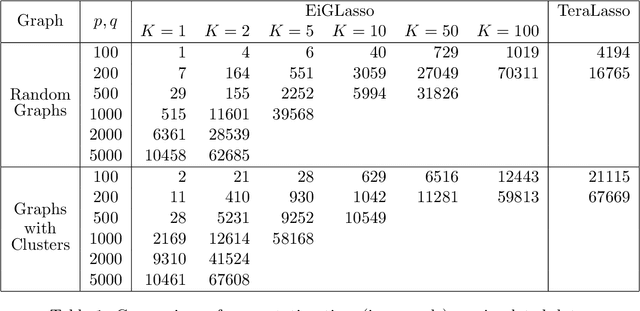
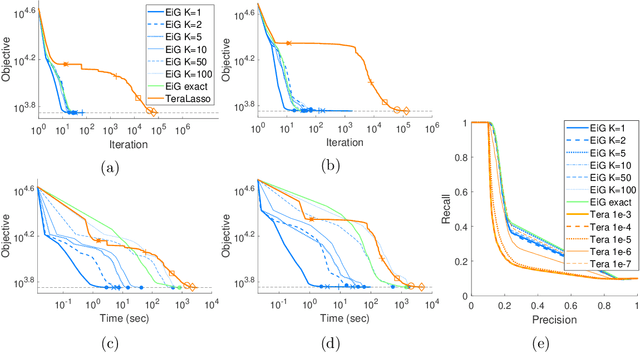
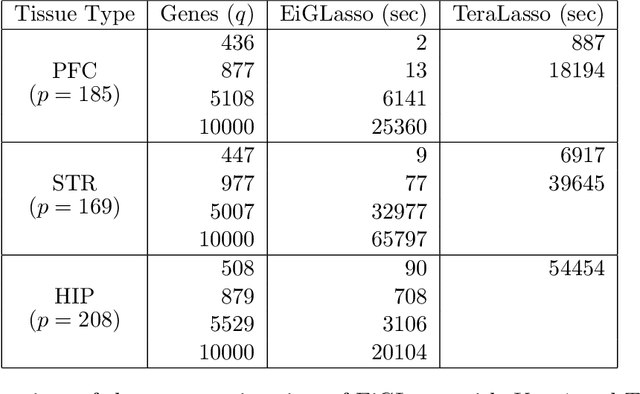
In many real-world problems, complex dependencies are present both among samples and among features. The Kronecker sum or the Cartesian product of two graphs, each modeling dependencies across features and across samples, has been used as an inverse covariance matrix for a matrix-variate Gaussian distribution, as an alternative to a Kronecker-product inverse covariance matrix, due to its more intuitive sparse structure. However, the existing methods for sparse Kronecker-sum inverse covariance estimation are limited in that they do not scale to more than a few hundred features and samples and that the unidentifiable parameters pose challenges in estimation. In this paper, we introduce EiGLasso, a highly scalable method for sparse Kronecker-sum inverse covariance estimation, based on Newton's method combined with eigendecomposition of the two graphs for exploiting the structure of Kronecker sum. EiGLasso further reduces computation time by approximating the Hessian based on the eigendecomposition of the sample and feature graphs. EiGLasso achieves quadratic convergence with the exact Hessian and linear convergence with the approximate Hessian. We describe a simple new approach to estimating the unidentifiable parameters that generalizes the existing methods. On simulated and real-world data, we demonstrate that EiGLasso achieves two to three orders-of-magnitude speed-up compared to the existing methods.

SEMULATOR: Emulating the Dynamics of Crossbar Array-based Analog Neural System with Regression Neural Networks

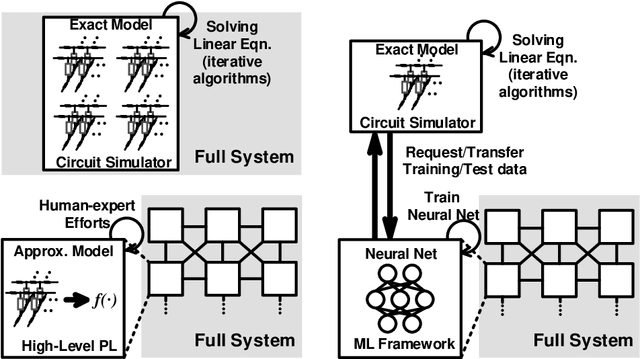
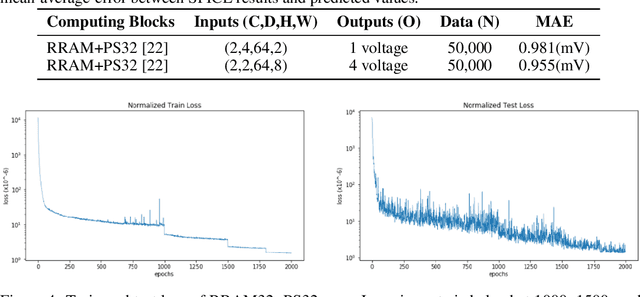
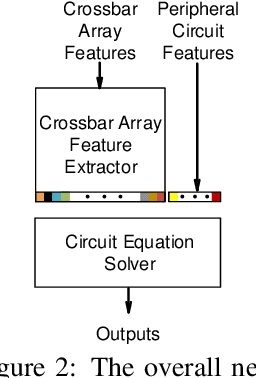
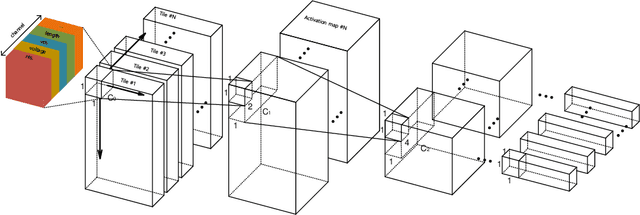
As deep neural networks require tremendous amount of computation and memory, analog computing with emerging memory devices is a promising alternative to digital computing for edge devices. However, because of the increasing simulation time for analog computing system, it has not been explored. To overcome this issue, analytically approximated simulators are developed, but these models are inaccurate and narrow down the options for peripheral circuits for multiply-accumulate operation (MAC). In this sense, we propose a methodology, SEMULATOR (SiMULATOR by Emulating the analog computing block) which uses a deep neural network to emulate the behavior of crossbar-based analog computing system. With the proposed neural architecture, we experimentally and theoretically shows that it emulates a MAC unit for neural computation. In addition, the simulation time is incomparably reduced when it compared to the circuit simulators such as SPICE.

Zero-shifting Technique for Deep Neural Network Training on Resistive Cross-point Arrays

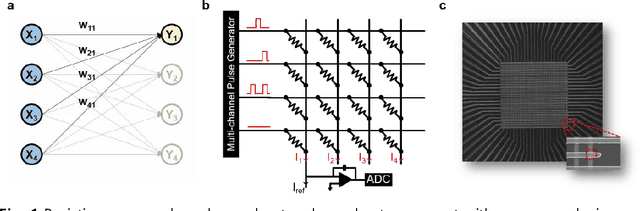
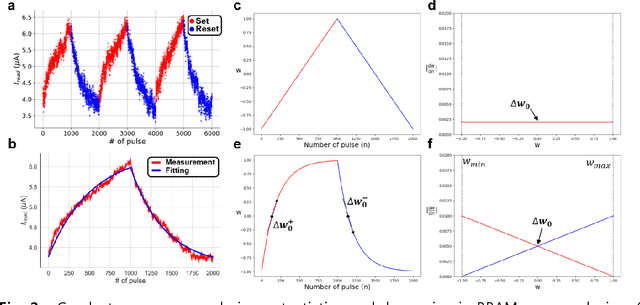
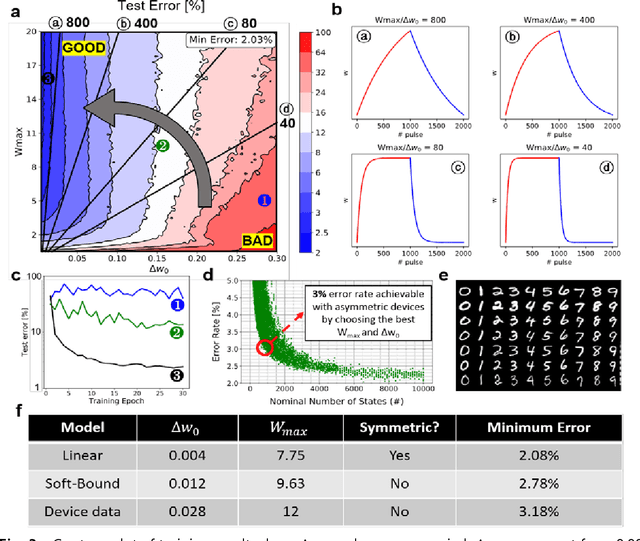
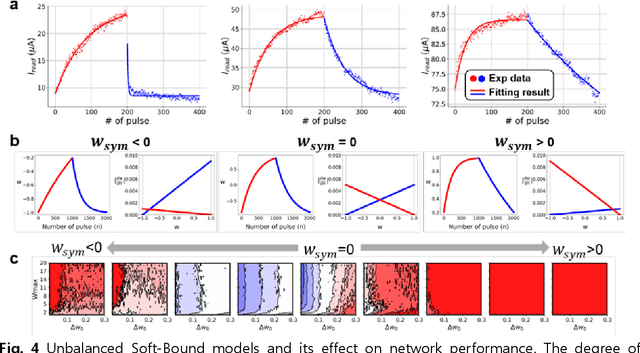
A resistive memory device-based computing architecture is one of the promising platforms for energy-efficient Deep Neural Network (DNN) training accelerators. The key technical challenge in realizing such accelerators is to accumulate the gradient information without a bias. Unlike the digital numbers in software which can be assigned and accessed with desired accuracy, numbers stored in resistive memory devices can only be manipulated following the physics of the device, which can significantly limit the training performance. Therefore, additional techniques and algorithm-level remedies are required to achieve the best possible performance in resistive memory device-based accelerators. In this paper, we analyze asymmetric conductance modulation characteristics in RRAM by Soft-bound synapse model and present an in-depth analysis on the relationship between device characteristics and DNN model accuracy using a 3-layer DNN trained on the MNIST dataset. We show that the imbalance between up and down update leads to a poor network performance. We introduce a concept of symmetry point and propose a zero-shifting technique which can compensate imbalance by programming the reference device and changing the zero value point of the weight. By using this zero-shifting method, we show that network performance dramatically improves for imbalanced synapse devices.

Analog CMOS-based Resistive Processing Unit for Deep Neural Network Training

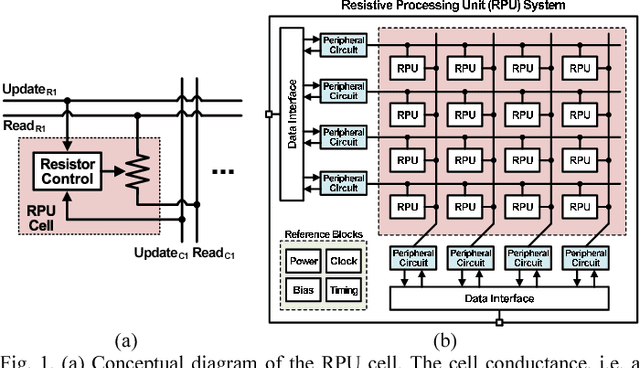
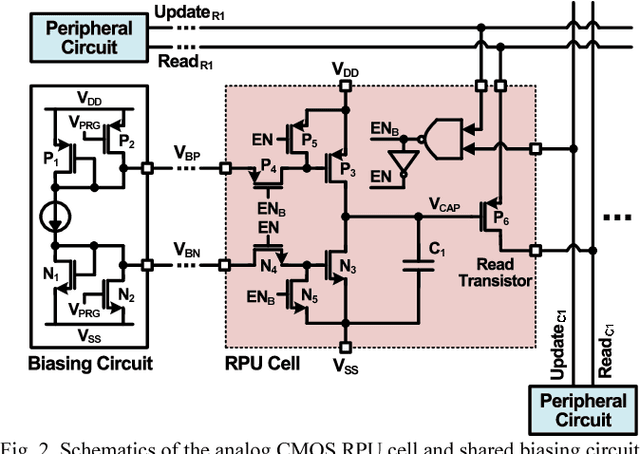
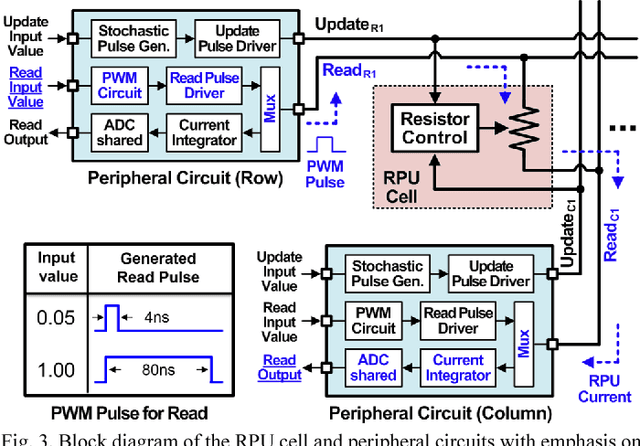
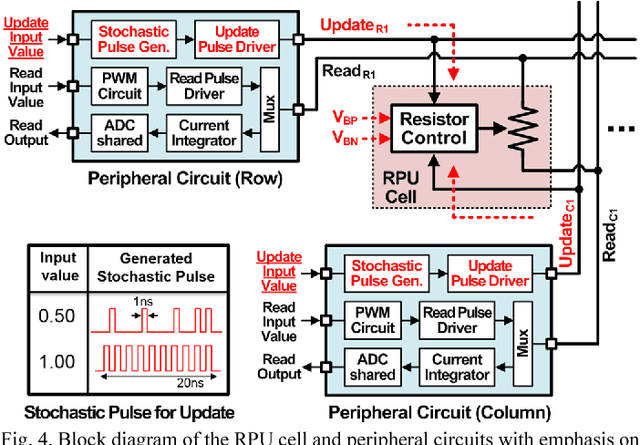
Recently we have shown that an architecture based on resistive processing unit (RPU) devices has potential to achieve significant acceleration in deep neural network (DNN) training compared to today's software-based DNN implementations running on CPU/GPU. However, currently available device candidates based on non-volatile memory technologies do not satisfy all the requirements to realize the RPU concept. Here, we propose an analog CMOS-based RPU design (CMOS RPU) which can store and process data locally and can be operated in a massively parallel manner. We analyze various properties of the CMOS RPU to evaluate the functionality and feasibility for acceleration of DNN training.

Large-Scale Optimization Algorithms for Sparse Conditional Gaussian Graphical Models

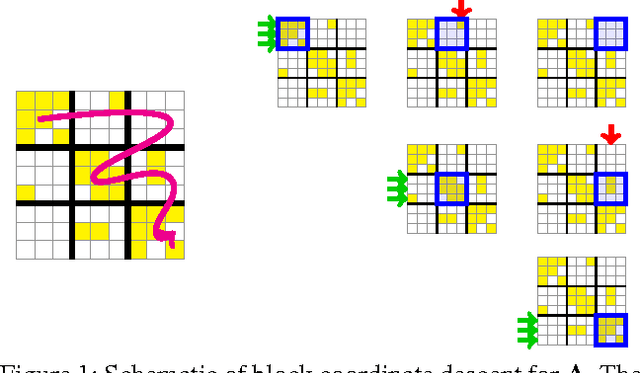
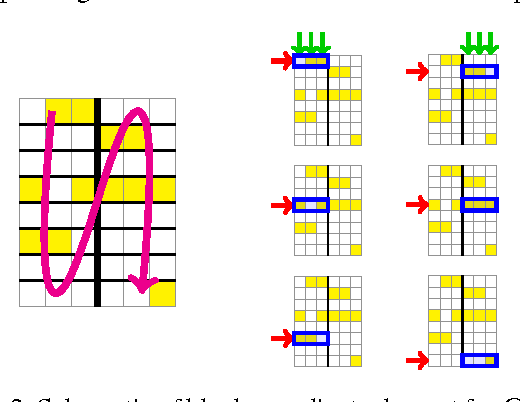
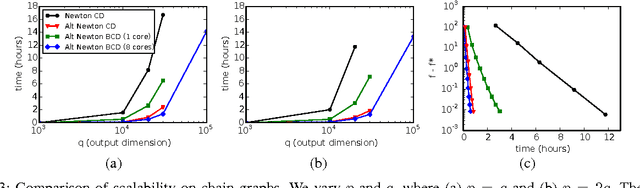
This paper addresses the problem of scalable optimization for L1-regularized conditional Gaussian graphical models. Conditional Gaussian graphical models generalize the well-known Gaussian graphical models to conditional distributions to model the output network influenced by conditioning input variables. While highly scalable optimization methods exist for sparse Gaussian graphical model estimation, state-of-the-art methods for conditional Gaussian graphical models are not efficient enough and more importantly, fail due to memory constraints for very large problems. In this paper, we propose a new optimization procedure based on a Newton method that efficiently iterates over two sub-problems, leading to drastic improvement in computation time compared to the previous methods. We then extend our method to scale to large problems under memory constraints, using block coordinate descent to limit memory usage while achieving fast convergence. Using synthetic and genomic data, we show that our methods can solve one million dimensional problems to high accuracy in a little over a day on a single machine.

Tree-guided group lasso for multi-response regression with structured sparsity, with an application to eQTL mapping

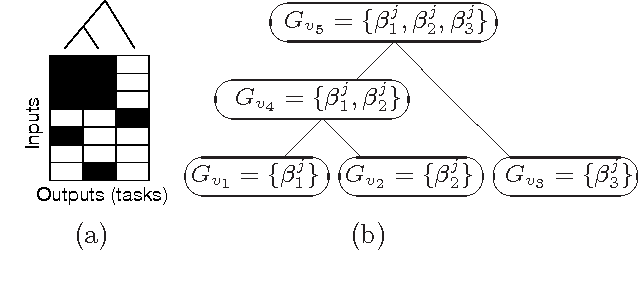
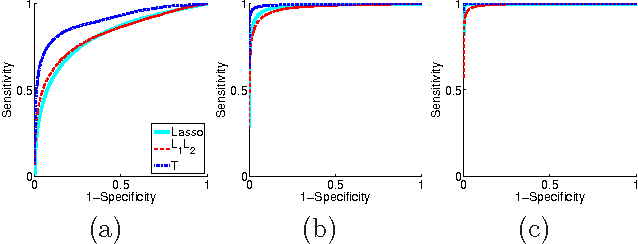
We consider the problem of estimating a sparse multi-response regression function, with an application to expression quantitative trait locus (eQTL) mapping, where the goal is to discover genetic variations that influence gene-expression levels. In particular, we investigate a shrinkage technique capable of capturing a given hierarchical structure over the responses, such as a hierarchical clustering tree with leaf nodes for responses and internal nodes for clusters of related responses at multiple granularity, and we seek to leverage this structure to recover covariates relevant to each hierarchically-defined cluster of responses. We propose a tree-guided group lasso, or tree lasso, for estimating such structured sparsity under multi-response regression by employing a novel penalty function constructed from the tree. We describe a systematic weighting scheme for the overlapping groups in the tree-penalty such that each regression coefficient is penalized in a balanced manner despite the inhomogeneous multiplicity of group memberships of the regression coefficients due to overlaps among groups. For efficient optimization, we employ a smoothing proximal gradient method that was originally developed for a general class of structured-sparsity-inducing penalties. Using simulated and yeast data sets, we demonstrate that our method shows a superior performance in terms of both prediction errors and recovery of true sparsity patterns, compared to other methods for learning a multivariate-response regression.

Smoothing proximal gradient method for general structured sparse regression

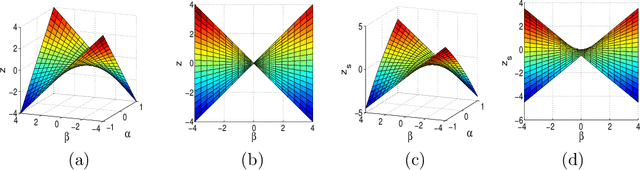
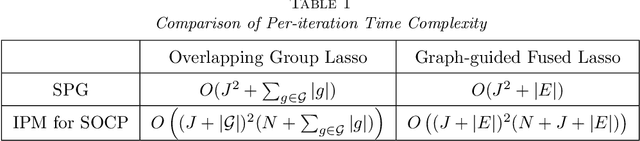
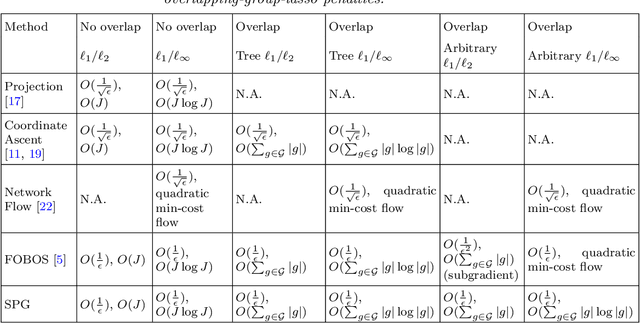
We study the problem of estimating high-dimensional regression models regularized by a structured sparsity-inducing penalty that encodes prior structural information on either the input or output variables. We consider two widely adopted types of penalties of this kind as motivating examples: (1) the general overlapping-group-lasso penalty, generalized from the group-lasso penalty; and (2) the graph-guided-fused-lasso penalty, generalized from the fused-lasso penalty. For both types of penalties, due to their nonseparability and nonsmoothness, developing an efficient optimization method remains a challenging problem. In this paper we propose a general optimization approach, the smoothing proximal gradient (SPG) method, which can solve structured sparse regression problems with any smooth convex loss under a wide spectrum of structured sparsity-inducing penalties. Our approach combines a smoothing technique with an effective proximal gradient method. It achieves a convergence rate significantly faster than the standard first-order methods, subgradient methods, and is much more scalable than the most widely used interior-point methods. The efficiency and scalability of our method are demonstrated on both simulation experiments and real genetic data sets.

Smoothing Proximal Gradient Method for General Structured Sparse Learning

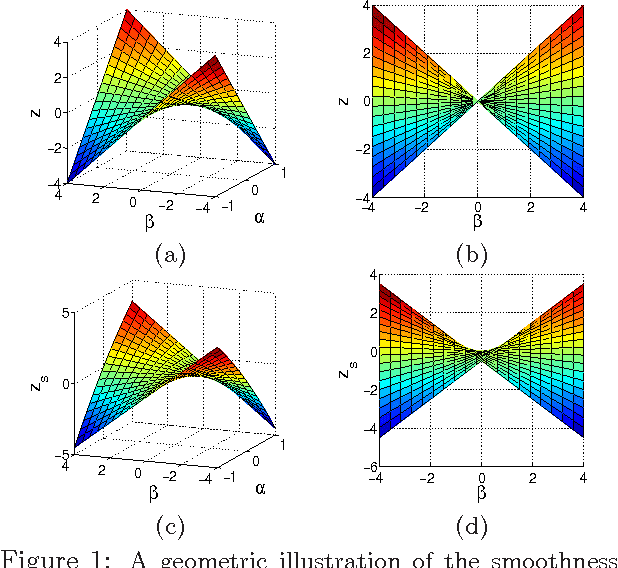
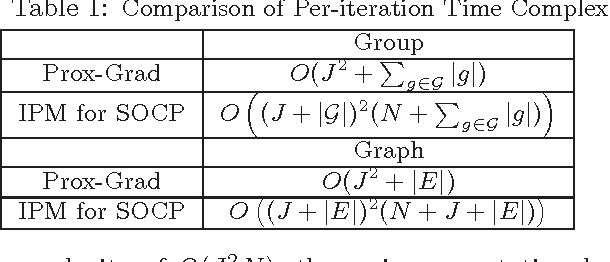
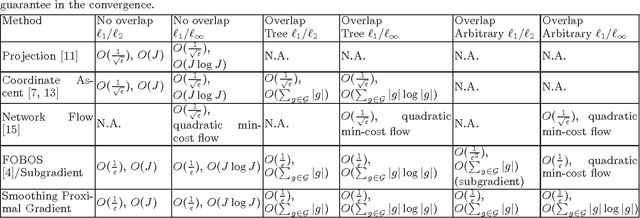
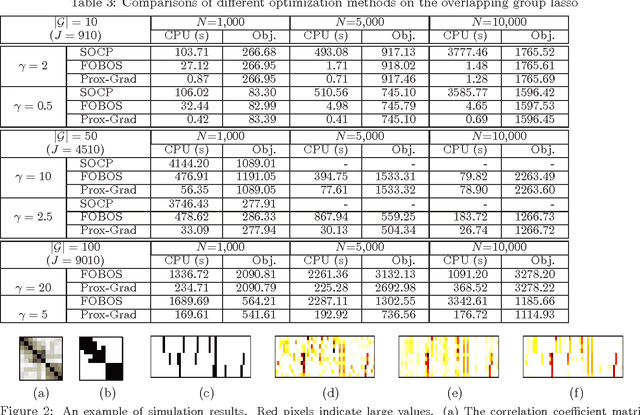
We study the problem of learning high dimensional regression models regularized by a structured-sparsity-inducing penalty that encodes prior structural information on either input or output sides. We consider two widely adopted types of such penalties as our motivating examples: 1) overlapping group lasso penalty, based on the l1/l2 mixed-norm penalty, and 2) graph-guided fusion penalty. For both types of penalties, due to their non-separability, developing an efficient optimization method has remained a challenging problem. In this paper, we propose a general optimization approach, called smoothing proximal gradient method, which can solve the structured sparse regression problems with a smooth convex loss and a wide spectrum of structured-sparsity-inducing penalties. Our approach is based on a general smoothing technique of Nesterov. It achieves a convergence rate faster than the standard first-order method, subgradient method, and is much more scalable than the most widely used interior-point method. Numerical results are reported to demonstrate the efficiency and scalability of the proposed method.

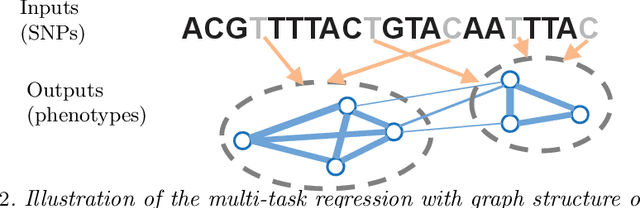
Graph-Structured Multi-task Regression and an Efficient Optimization Method for General Fused Lasso

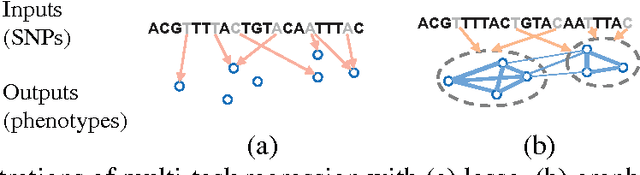
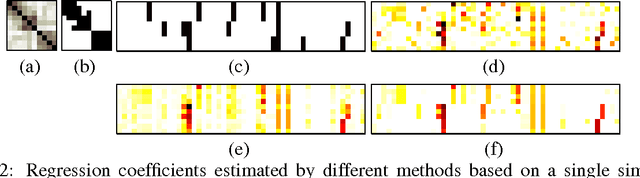
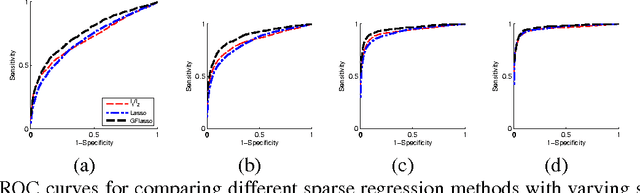
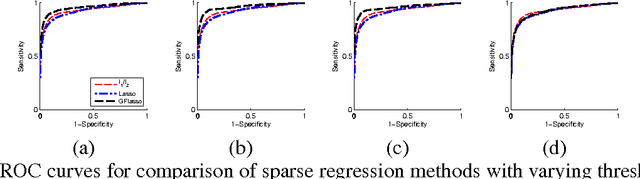
We consider the problem of learning a structured multi-task regression, where the output consists of multiple responses that are related by a graph and the correlated response variables are dependent on the common inputs in a sparse but synergistic manner. Previous methods such as l1/l2-regularized multi-task regression assume that all of the output variables are equally related to the inputs, although in many real-world problems, outputs are related in a complex manner. In this paper, we propose graph-guided fused lasso (GFlasso) for structured multi-task regression that exploits the graph structure over the output variables. We introduce a novel penalty function based on fusion penalty to encourage highly correlated outputs to share a common set of relevant inputs. In addition, we propose a simple yet efficient proximal-gradient method for optimizing GFlasso that can also be applied to any optimization problems with a convex smooth loss and the general class of fusion penalty defined on arbitrary graph structures. By exploiting the structure of the non-smooth ''fusion penalty'', our method achieves a faster convergence rate than the standard first-order method, sub-gradient method, and is significantly more scalable than the widely adopted second-order cone-programming and quadratic-programming formulations. In addition, we provide an analysis of the consistency property of the GFlasso model. Experimental results not only demonstrate the superiority of GFlasso over the standard lasso but also show the efficiency and scalability of our proximal-gradient method.