On Convergence of the Alternating Directions SGHMC Algorithm

We study convergence rates of Hamiltonian Monte Carlo (HMC) algorithms with leapfrog integration under mild conditions on stochastic gradient oracle for the target distribution (SGHMC). Our method extends standard HMC by allowing the use of general auxiliary distributions, which is achieved by a novel procedure of Alternating Directions. The convergence analysis is based on the investigations of the Dirichlet forms associated with the underlying Markov chain driving the algorithms. For this purpose, we provide a detailed analysis on the error of the leapfrog integrator for Hamiltonian motions with both the kinetic and potential energy functions in general form. We characterize the explicit dependence of the convergence rates on key parameters such as the problem dimension, functional properties of both the target and auxiliary distributions, and the quality of the oracle.

On Representations of Mean-Field Variational Inference

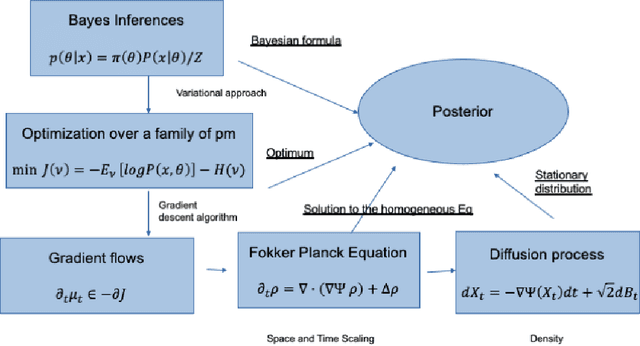
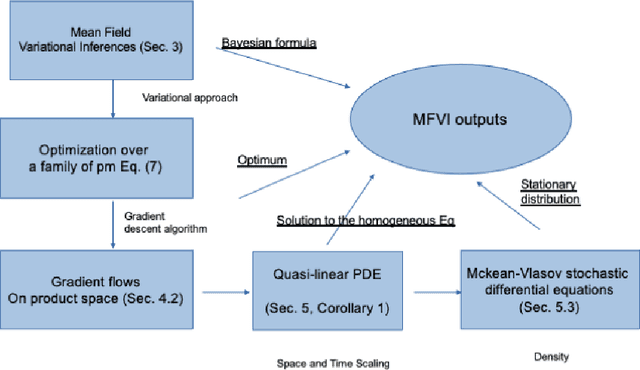
The mean field variational inference (MFVI) formulation restricts the general Bayesian inference problem to the subspace of product measures. We present a framework to analyze MFVI algorithms, which is inspired by a similar development for general variational Bayesian formulations. Our approach enables the MFVI problem to be represented in three different manners: a gradient flow on Wasserstein space, a system of Fokker-Planck-like equations and a diffusion process. Rigorous guarantees are established to show that a time-discretized implementation of the coordinate ascent variational inference algorithm in the product Wasserstein space of measures yields a gradient flow in the limit. A similar result is obtained for their associated densities, with the limit being given by a quasi-linear partial differential equation. A popular class of practical algorithms falls in this framework, which provides tools to establish convergence. We hope this framework could be used to guarantee convergence of algorithms in a variety of approaches, old and new, to solve variational inference problems.

Neural Network Training with Asymmetric Crosspoint Elements

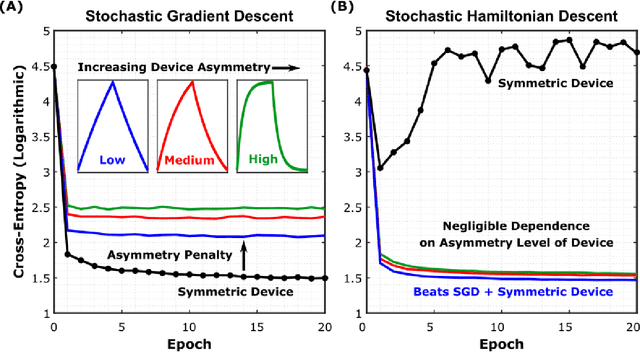
Analog crossbar arrays comprising programmable nonvolatile resistors are under intense investigation for acceleration of deep neural network training. However, the ubiquitous asymmetric conductance modulation of practical resistive devices critically degrades the classification performance of networks trained with conventional algorithms. Here, we describe and experimentally demonstrate an alternative fully-parallel training algorithm: Stochastic Hamiltonian Descent. Instead of conventionally tuning weights in the direction of the error function gradient, this method programs the network parameters to successfully minimize the total energy (Hamiltonian) of the system that incorporates the effects of device asymmetry. We provide critical intuition on why device asymmetry is fundamentally incompatible with conventional training algorithms and how the new approach exploits it as a useful feature instead. Our technique enables immediate realization of analog deep learning accelerators based on readily available device technologies.

Hamiltonian Monte Carlo with Asymmetrical Momentum Distributions

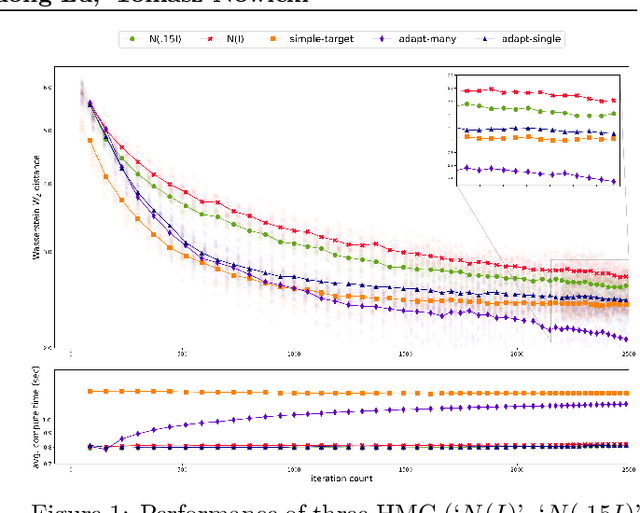
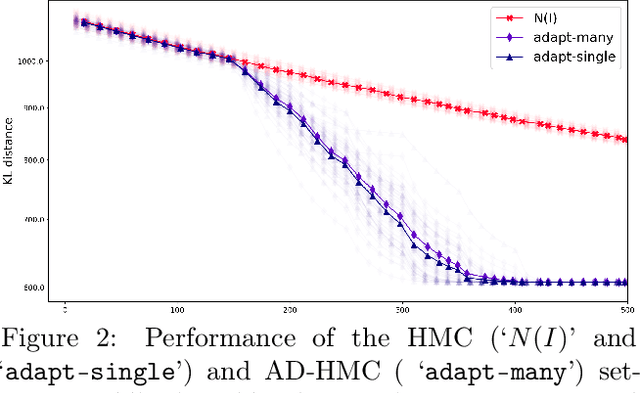
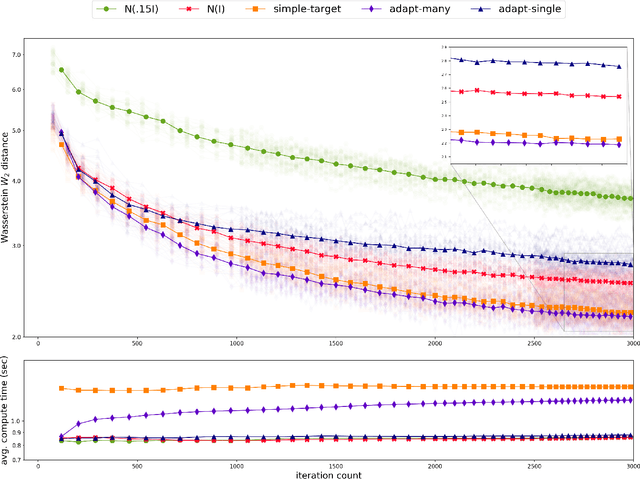
Existing rigorous convergence guarantees for the Hamiltonian Monte Carlo (HMC) algorithm use Gaussian auxiliary momentum variables, which are crucially symmetrically distributed. We present a novel convergence analysis for HMC utilizing new analytic and probabilistic arguments. The convergence is rigorously established under significantly weaker conditions, which among others allow for general auxiliary distributions. In our framework, we show that plain HMC with asymmetrical momentum distributions breaks a key self-adjointness requirement. We propose a modified version that we call the Alternating Direction HMC (AD-HMC). Sufficient conditions are established under which AD-HMC exhibits geometric convergence in Wasserstein distance. Numerical experiments suggest that AD-HMC can show improved performance over HMC with Gaussian auxiliaries.

HMC, an Algorithms in Data Mining, the Functional Analysis approach

The main purpose of this paper is to facilitate the communication between the Analytic, Probabilistic and Algorithmic communities. We present a proof of convergence of the Hamiltonian (Hybrid) Monte Carlo algorithm from the point of view of the Dynamical Systems, where the evolving objects are densities of probability distributions and the tool are derived from the Functional Analysis.

HMC, an example of Functional Analysis applied to Algorithms in Data Mining. The convergence in $L^p$

We present a proof of convergence of the Hamiltonian Monte Carlo algorithm in terms of Functional Analysis. We represent the algorithm as an operator on the density functions, and prove the convergence of iterations of this operator in $L^p$, for $1<p<\infty$, and strong convergence for $2\le p<\infty$.