DIVIDE: A Framework for Learning from Independent Multi-Mechanism Data Using Deep Encoders and Gaussian Processes

Scientific datasets often arise from multiple independent mechanisms such as spatial, categorical or structural effects, whose combined influence obscures their individual contributions. We introduce DIVIDE, a framework that disentangles these influences by integrating mechanism-specific deep encoders with a structured Gaussian Process in a joint latent space. Disentanglement here refers to separating independently acting generative factors. The encoders isolate distinct mechanisms while the Gaussian Process captures their combined effect with calibrated uncertainty. The architecture supports structured priors, enabling interpretable and mechanism-aware prediction as well as efficient active learning. DIVIDE is demonstrated on synthetic datasets combining categorical image patches with nonlinear spatial fields, on FerroSIM spin lattice simulations of ferroelectric patterns, and on experimental PFM hysteresis loops from PbTiO3 films. Across benchmarks, DIVIDE separates mechanisms, reproduces additive and scaled interactions, and remains robust under noise. The framework extends naturally to multifunctional datasets where mechanical, electromagnetic or optical responses coexist.

Invariant Discovery of Features Across Multiple Length Scales: Applications in Microscopy and Autonomous Materials Characterization

Physical imaging is a foundational characterization method in areas from condensed matter physics and chemistry to astronomy and spans length scales from atomic to universe. Images encapsulate crucial data regarding atomic bonding, materials microstructures, and dynamic phenomena such as microstructural evolution and turbulence, among other phenomena. The challenge lies in effectively extracting and interpreting this information. Variational Autoencoders (VAEs) have emerged as powerful tools for identifying underlying factors of variation in image data, providing a systematic approach to distilling meaningful patterns from complex datasets. However, a significant hurdle in their application is the definition and selection of appropriate descriptors reflecting local structure. Here we introduce the scale-invariant VAE approach (SI-VAE) based on the progressive training of the VAE with the descriptors sampled at different length scales. The SI-VAE allows the discovery of the length scale dependent factors of variation in the system. Here, we illustrate this approach using the ferroelectric domain images and generalize it to the movies of the electron-beam induced phenomena in graphene and topography evolution across combinatorial libraries. This approach can further be used to initialize the decision making in automated experiments including structure-property discovery and can be applied across a broad range of imaging methods. This approach is universal and can be applied to any spatially resolved data including both experimental imaging studies and simulations, and can be particularly useful for exploration of phenomena such as turbulence, scale-invariant transformation fronts, etc.

Learning and Controlling Silicon Dopant Transitions in Graphene using Scanning Transmission Electron Microscopy

We introduce a machine learning approach to determine the transition dynamics of silicon atoms on a single layer of carbon atoms, when stimulated by the electron beam of a scanning transmission electron microscope (STEM). Our method is data-centric, leveraging data collected on a STEM. The data samples are processed and filtered to produce symbolic representations, which we use to train a neural network to predict transition probabilities. These learned transition dynamics are then leveraged to guide a single silicon atom throughout the lattice to pre-determined target destinations. We present empirical analyses that demonstrate the efficacy and generality of our approach.

Physics and Chemistry from Parsimonious Representations: Image Analysis via Invariant Variational Autoencoders

Electron, optical, and scanning probe microscopy methods are generating ever increasing volume of image data containing information on atomic and mesoscale structures and functionalities. This necessitates the development of the machine learning methods for discovery of physical and chemical phenomena from the data, such as manifestations of symmetry breaking in electron and scanning tunneling microscopy images, variability of the nanoparticles. Variational autoencoders (VAEs) are emerging as a powerful paradigm for the unsupervised data analysis, allowing to disentangle the factors of variability and discover optimal parsimonious representation. Here, we summarize recent developments in VAEs, covering the basic principles and intuition behind the VAEs. The invariant VAEs are introduced as an approach to accommodate scale and translation invariances present in imaging data and separate known factors of variations from the ones to be discovered. We further describe the opportunities enabled by the control over VAE architecture, including conditional, semi-supervised, and joint VAEs. Several case studies of VAE applications for toy models and experimental data sets in Scanning Transmission Electron Microscopy are discussed, emphasizing the deep connection between VAE and basic physical principles. All the codes used here are available at https://github.com/saimani5/VAE-tutorials and this article can be used as an application guide when applying these to own data sets.

Robust Feature Disentanglement in Imaging Data via Joint Invariant Variational Autoencoders: from Cards to Atoms

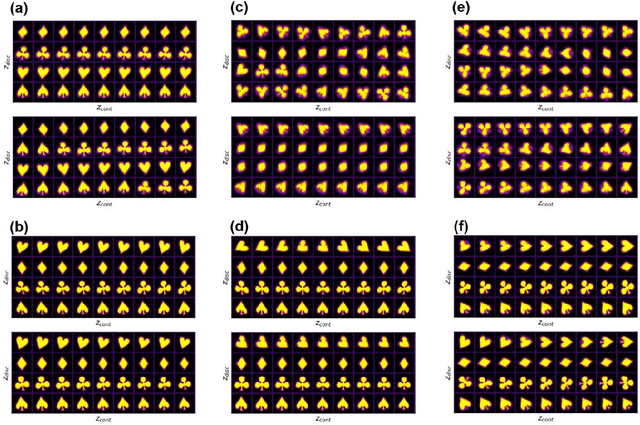
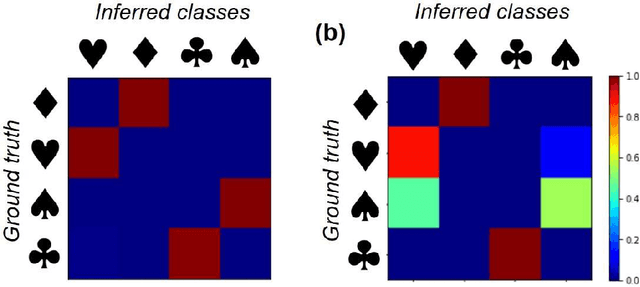
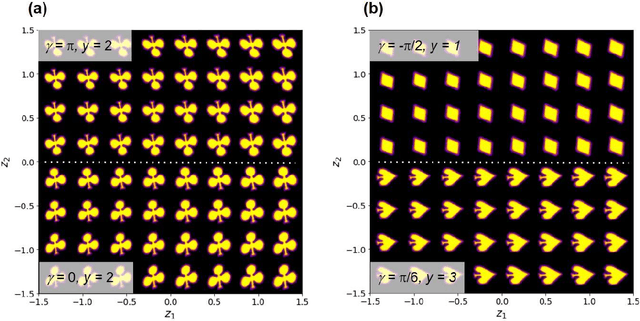
Recent advances in imaging from celestial objects in astronomy visualized via optical and radio telescopes to atoms and molecules resolved via electron and probe microscopes are generating immense volumes of imaging data, containing information about the structure of the universe from atomic to astronomic levels. The classical deep convolutional neural network architectures traditionally perform poorly on the data sets having a significant orientational disorder, that is, having multiple copies of the same or similar object in arbitrary orientation in the image plane. Similarly, while clustering methods are well suited for classification into discrete classes and manifold learning and variational autoencoders methods can disentangle representations of the data, the combined problem is ill-suited to a classical non-supervised learning paradigm. Here we introduce a joint rotationally (and translationally) invariant variational autoencoder (j-trVAE) that is ideally suited to the solution of such a problem. The performance of this method is validated on several synthetic data sets and extended to high-resolution imaging data of electron and scanning probe microscopy. We show that latent space behaviors directly comport to the known physics of ferroelectric materials and quantum systems. We further note that the engineering of the latent space structure via imposed topological structure or directed graph relationship allows for applications in topological discovery and causal physical learning.