Weakly Supervised Semantic Parsing with Execution-based Spurious Program Filtering

The problem of spurious programs is a longstanding challenge when training a semantic parser from weak supervision. To eliminate such programs that have wrong semantics but correct denotation, existing methods focus on exploiting similarities between examples based on domain-specific knowledge. In this paper, we propose a domain-agnostic filtering mechanism based on program execution results. Specifically, for each program obtained through the search process, we first construct a representation that captures the program's semantics as execution results under various inputs. Then, we run a majority vote on these representations to identify and filter out programs with significantly different semantics from the other programs. In particular, our method is orthogonal to the program search process so that it can easily augment any of the existing weakly supervised semantic parsing frameworks. Empirical evaluations on the Natural Language Visual Reasoning and WikiTableQuestions demonstrate that applying our method to the existing semantic parsers induces significantly improved performances.

Asking Clarification Questions to Handle Ambiguity in Open-Domain QA

Ambiguous questions persist in open-domain question answering, because formulating a precise question with a unique answer is often challenging. Previously, Min et al. (2020) have tackled this issue by generating disambiguated questions for all possible interpretations of the ambiguous question. This can be effective, but not ideal for providing an answer to the user. Instead, we propose to ask a clarification question, where the user's response will help identify the interpretation that best aligns with the user's intention. We first present CAMBIGNQ, a dataset consisting of 5,654 ambiguous questions, each with relevant passages, possible answers, and a clarification question. The clarification questions were efficiently created by generating them using InstructGPT and manually revising them as necessary. We then define a pipeline of tasks and design appropriate evaluation metrics. Lastly, we achieve 61.3 F1 on ambiguity detection and 40.5 F1 on clarification-based QA, providing strong baselines for future work.

Neural Sequence-to-grid Module for Learning Symbolic Rules

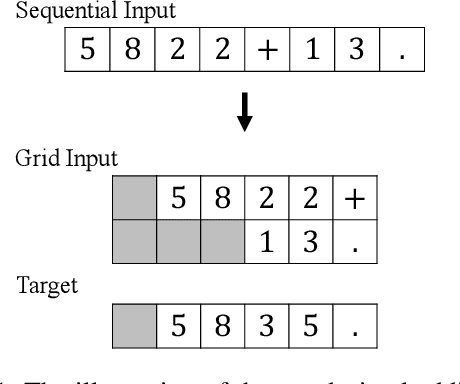
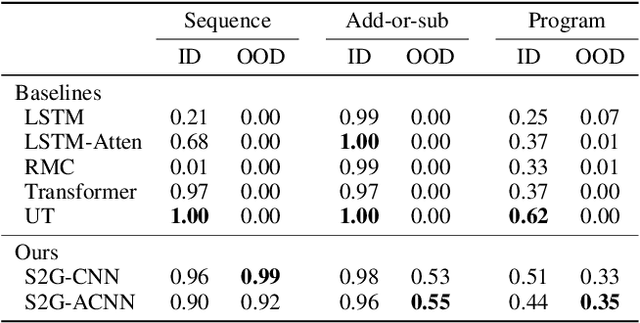
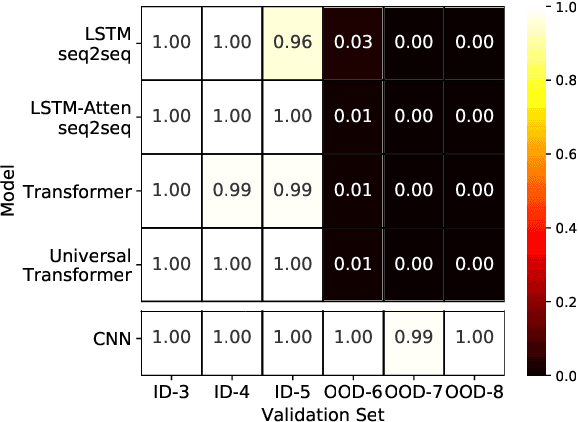
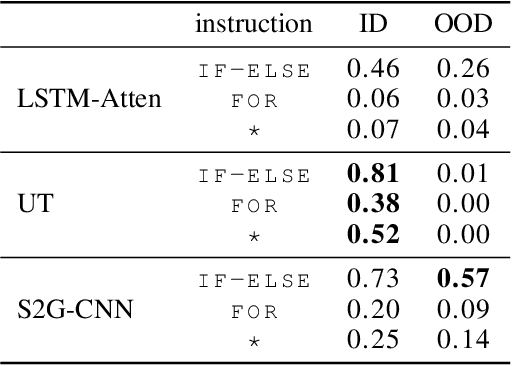
Logical reasoning tasks over symbols, such as learning arithmetic operations and computer program evaluations, have become challenges to deep learning. In particular, even state-of-the-art neural networks fail to achieve \textit{out-of-distribution} (OOD) generalization of symbolic reasoning tasks, whereas humans can easily extend learned symbolic rules. To resolve this difficulty, we propose a neural sequence-to-grid (seq2grid) module, an input preprocessor that automatically segments and aligns an input sequence into a grid. As our module outputs a grid via a novel differentiable mapping, any neural network structure taking a grid input, such as ResNet or TextCNN, can be jointly trained with our module in an end-to-end fashion. Extensive experiments show that neural networks having our module as an input preprocessor achieve OOD generalization on various arithmetic and algorithmic problems including number sequence prediction problems, algebraic word problems, and computer program evaluation problems while other state-of-the-art sequence transduction models cannot. Moreover, we verify that our module enhances TextCNN to solve the bAbI QA tasks without external memory.

Number Sequence Prediction Problems and Computational Powers of Neural Network Models

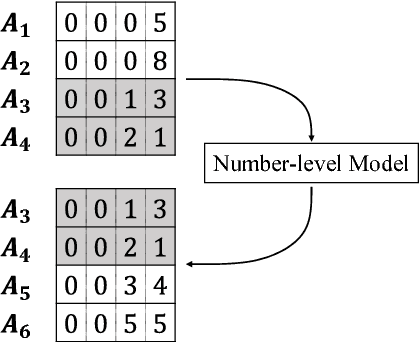
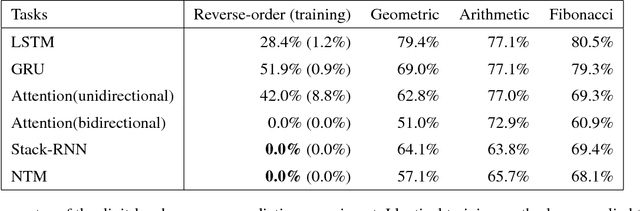
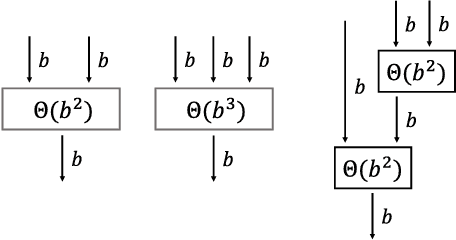
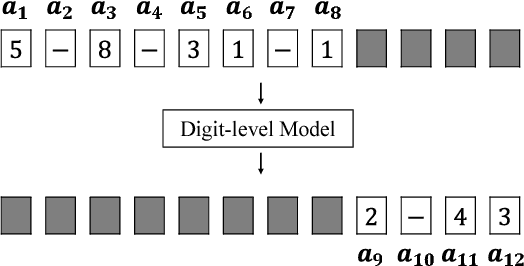
Inspired by number series tests to measure human intelligence, we suggest number sequence prediction tasks to assess neural network models' computational powers for solving algorithmic problems. We define complexity and difficulty of a number sequence prediction task with the structure of the smallest automation that can generate the sequence. We suggest two types of number sequence prediction problems: the number-level and the digit-level problems. The number-level problems format sequences as 2-dimensional grids of digits, and the digit-level problem provides a single digit input per a time step, hence solving this problem is equivalent to modeling a sequential state automation. The complexity of a number-level sequence problem can be defined with the depth of an equivalent combinatorial logic. Experimental results with CNN models suggest that they are capable of learning the compound operations of the number-level sequence generation rules but the depths of the compound operations are limited. For the digit-level problems, GRU and LSTM models can solve the problems with complexity of finite state automations, but they cannot solve the problems with complexity of pushdown automations or Turing machines. The results show that our number sequence prediction problems effectively evaluate machine learning models' computational capabilities.