Neural Attention Memory

We propose a novel perspective of the attention mechanism by reinventing it as a memory architecture for neural networks, namely Neural Attention Memory (NAM). NAM is a memory structure that is both readable and writable via differentiable linear algebra operations. We explore three use cases of NAM: memory-augmented neural network (MANN), few-shot learning, and efficient long-range attention. First, we design two NAM-based MANNs of Long Short-term Memory (LSAM) and NAM Turing Machine (NAM-TM) that show better computational powers in algorithmic zero-shot generalization tasks compared to other baselines such as differentiable neural computer (DNC). Next, we apply NAM to the N-way K-shot learning task and show that it is more effective at reducing false positives compared to the baseline cosine classifier. Finally, we implement an efficient Transformer with NAM and evaluate it with long-range arena tasks to show that NAM can be an efficient and effective alternative for scaled dot-product attention.

Defensive ML: Defending Architectural Side-channels with Adversarial Obfuscation

Side-channel attacks that use machine learning (ML) for signal analysis have become prominent threats to computer security, as ML models easily find patterns in signals. To address this problem, this paper explores using Adversarial Machine Learning (AML) methods as a defense at the computer architecture layer to obfuscate side channels. We call this approach Defensive ML, and the generator to obfuscate signals, defender. Defensive ML is a workflow to design, implement, train, and deploy defenders for different environments. First, we design a defender architecture given the physical characteristics and hardware constraints of the side-channel. Next, we use our DefenderGAN structure to train the defender. Finally, we apply defensive ML to thwart two side-channel attacks: one based on memory contention and the other on application power. The former uses a hardware defender with ns-level response time that attains a high level of security with half the performance impact of a traditional scheme; the latter uses a software defender with ms-level response time that provides better security than a traditional scheme with only 70% of its power overhead.

Neural Sequence-to-grid Module for Learning Symbolic Rules

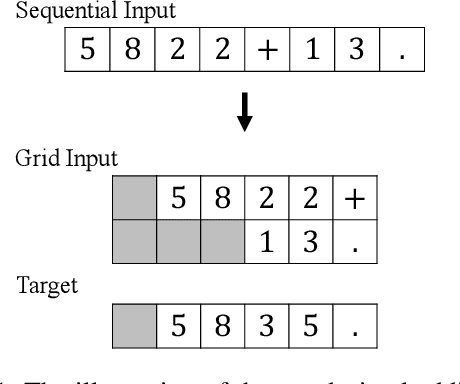
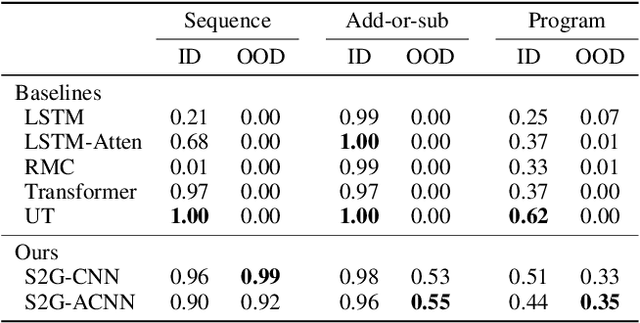
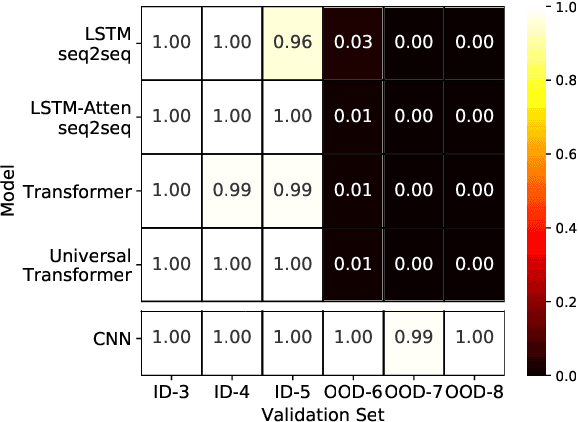
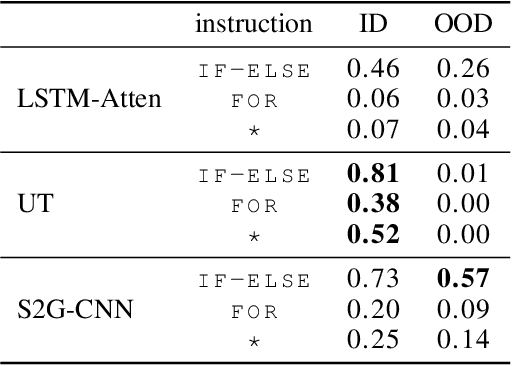
Logical reasoning tasks over symbols, such as learning arithmetic operations and computer program evaluations, have become challenges to deep learning. In particular, even state-of-the-art neural networks fail to achieve \textit{out-of-distribution} (OOD) generalization of symbolic reasoning tasks, whereas humans can easily extend learned symbolic rules. To resolve this difficulty, we propose a neural sequence-to-grid (seq2grid) module, an input preprocessor that automatically segments and aligns an input sequence into a grid. As our module outputs a grid via a novel differentiable mapping, any neural network structure taking a grid input, such as ResNet or TextCNN, can be jointly trained with our module in an end-to-end fashion. Extensive experiments show that neural networks having our module as an input preprocessor achieve OOD generalization on various arithmetic and algorithmic problems including number sequence prediction problems, algebraic word problems, and computer program evaluation problems while other state-of-the-art sequence transduction models cannot. Moreover, we verify that our module enhances TextCNN to solve the bAbI QA tasks without external memory.

I-BERT: Inductive Generalization of Transformer to Arbitrary Context Lengths

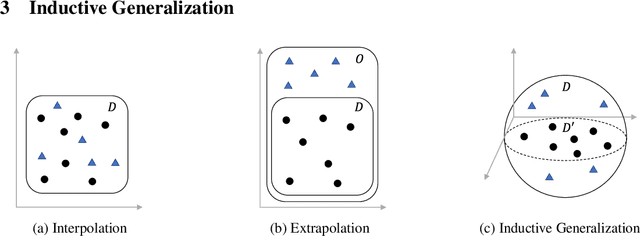
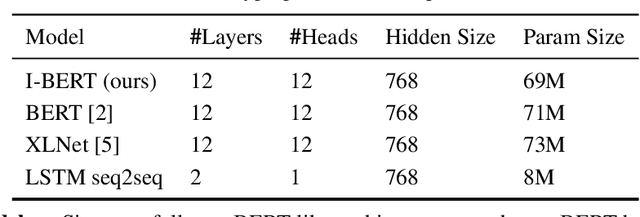
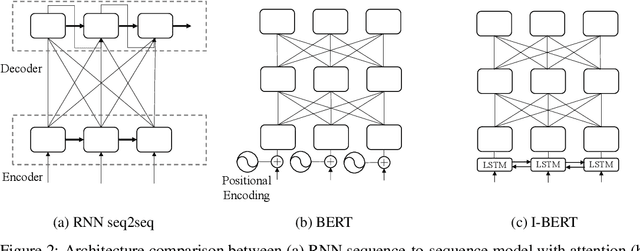
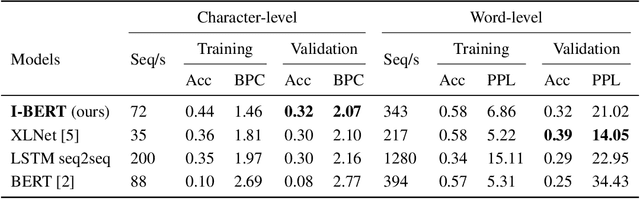
Self-attention has emerged as a vital component of state-of-the-art sequence-to-sequence models for natural language processing in recent years, brought to the forefront by pre-trained bi-directional Transformer models. Its effectiveness is partly due to its non-sequential architecture, which promotes scalability and parallelism but limits the model to inputs of a bounded length. In particular, such architectures perform poorly on algorithmic tasks, where the model must learn a procedure which generalizes to input lengths unseen in training, a capability we refer to as inductive generalization. Identifying the computational limits of existing self-attention mechanisms, we propose I-BERT, a bi-directional Transformer that replaces positional encodings with a recurrent layer. The model inductively generalizes on a variety of algorithmic tasks where state-of-the-art Transformer models fail to do so. We also test our method on masked language modeling tasks where training and validation sets are partitioned to verify inductive generalization. Out of three algorithmic and two natural language inductive generalization tasks, I-BERT achieves state-of-the-art results on four tasks.

Number Sequence Prediction Problems and Computational Powers of Neural Network Models

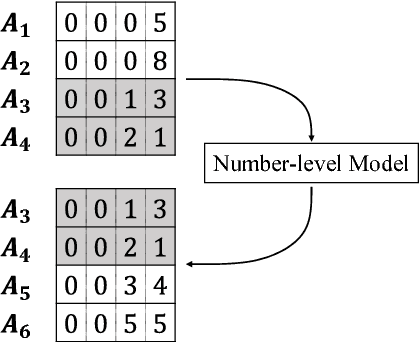
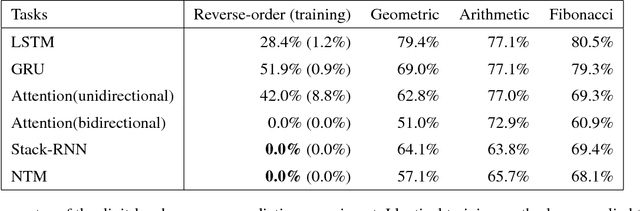
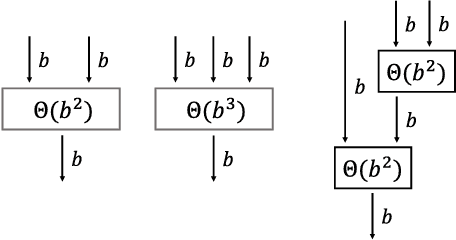
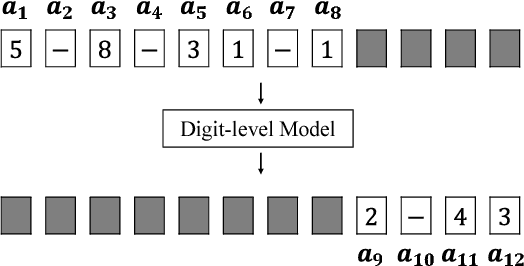
Inspired by number series tests to measure human intelligence, we suggest number sequence prediction tasks to assess neural network models' computational powers for solving algorithmic problems. We define complexity and difficulty of a number sequence prediction task with the structure of the smallest automation that can generate the sequence. We suggest two types of number sequence prediction problems: the number-level and the digit-level problems. The number-level problems format sequences as 2-dimensional grids of digits, and the digit-level problem provides a single digit input per a time step, hence solving this problem is equivalent to modeling a sequential state automation. The complexity of a number-level sequence problem can be defined with the depth of an equivalent combinatorial logic. Experimental results with CNN models suggest that they are capable of learning the compound operations of the number-level sequence generation rules but the depths of the compound operations are limited. For the digit-level problems, GRU and LSTM models can solve the problems with complexity of finite state automations, but they cannot solve the problems with complexity of pushdown automations or Turing machines. The results show that our number sequence prediction problems effectively evaluate machine learning models' computational capabilities.