Proper vs Improper Quantum PAC learning

A basic question in the PAC model of learning is whether proper learning is harder than improper learning. In the classical case, there are examples of concept classes with VC dimension $d$ that have sample complexity $\Omega\left(\frac d\epsilon\log\frac1\epsilon\right)$ for proper learning with error $\epsilon$, while the complexity for improper learning is O$\!\left(\frac d\epsilon\right)$. One such example arises from the Coupon Collector problem. Motivated by the efficiency of proper versus improper learning with quantum samples, Arunachalam, Belovs, Childs, Kothari, Rosmanis, and de Wolf (TQC 2020) studied an analogue, the Quantum Coupon Collector problem. Curiously, they discovered that for learning size $k$ subsets of $[n]$ the problem has sample complexity $\Theta(k\log\min\{k,n-k+1\})$, in contrast with the complexity of $\Theta(k\log k)$ for Coupon Collector. This effectively negates the possibility of a separation between the two modes of learning via the quantum problem, and Arunachalam et al.\ posed the possibility of such a separation as an open question. In this work, we first present an algorithm for the Quantum Coupon Collector problem with sample complexity that matches the sharper lower bound of $(1-o_k(1))k\ln\min\{k,n-k+1\}$ shown recently by Bab Hadiashar, Nayak, and Sinha (IEEE TIT 2024), for the entire range of the parameter $k$. Next, we devise a variant of the problem, the Quantum Padded Coupon Collector. We prove that its sample complexity matches that of the classical Coupon Collector problem for both modes of learning, thereby exhibiting the same asymptotic separation between proper and improper quantum learning as mentioned above. The techniques we develop in the process can be directly applied to any form of padded quantum data. We hope that padding can more generally lift other forms of classical learning behaviour to the quantum setting.

Methods to Estimate Large Language Model Confidence

Large Language Models have difficulty communicating uncertainty, which is a significant obstacle to applying LLMs to complex medical tasks. This study evaluates methods to measure LLM confidence when suggesting a diagnosis for challenging clinical vignettes. GPT4 was asked a series of challenging case questions using Chain of Thought and Self Consistency prompting. Multiple methods were investigated to assess model confidence and evaluated on their ability to predict the models observed accuracy. The methods evaluated were Intrinsic Confidence, SC Agreement Frequency and CoT Response Length. SC Agreement Frequency correlated with observed accuracy, yielding a higher Area under the Receiver Operating Characteristic Curve compared to Intrinsic Confidence and CoT Length analysis. SC agreement is the most useful proxy for model confidence, especially for medical diagnosis. Model Intrinsic Confidence and CoT Response Length exhibit a weaker ability to differentiate between correct and incorrect answers, preventing them from being reliable and interpretable markers for model confidence. We conclude GPT4 has a limited ability to assess its own diagnostic accuracy. SC Agreement Frequency is the most useful method to measure GPT4 confidence.

MedAlign: A Clinician-Generated Dataset for Instruction Following with Electronic Medical Records

The ability of large language models (LLMs) to follow natural language instructions with human-level fluency suggests many opportunities in healthcare to reduce administrative burden and improve quality of care. However, evaluating LLMs on realistic text generation tasks for healthcare remains challenging. Existing question answering datasets for electronic health record (EHR) data fail to capture the complexity of information needs and documentation burdens experienced by clinicians. To address these challenges, we introduce MedAlign, a benchmark dataset of 983 natural language instructions for EHR data. MedAlign is curated by 15 clinicians (7 specialities), includes clinician-written reference responses for 303 instructions, and provides 276 longitudinal EHRs for grounding instruction-response pairs. We used MedAlign to evaluate 6 general domain LLMs, having clinicians rank the accuracy and quality of each LLM response. We found high error rates, ranging from 35% (GPT-4) to 68% (MPT-7B-Instruct), and an 8.3% drop in accuracy moving from 32k to 2k context lengths for GPT-4. Finally, we report correlations between clinician rankings and automated natural language generation metrics as a way to rank LLMs without human review. We make MedAlign available under a research data use agreement to enable LLM evaluations on tasks aligned with clinician needs and preferences.

Diagnostic Reasoning Prompts Reveal the Potential for Large Language Model Interpretability in Medicine

One of the major barriers to using large language models (LLMs) in medicine is the perception they use uninterpretable methods to make clinical decisions that are inherently different from the cognitive processes of clinicians. In this manuscript we develop novel diagnostic reasoning prompts to study whether LLMs can perform clinical reasoning to accurately form a diagnosis. We find that GPT4 can be prompted to mimic the common clinical reasoning processes of clinicians without sacrificing diagnostic accuracy. This is significant because an LLM that can use clinical reasoning to provide an interpretable rationale offers physicians a means to evaluate whether LLMs can be trusted for patient care. Novel prompting methods have the potential to expose the black box of LLMs, bringing them one step closer to safe and effective use in medicine.

Optimal lower bounds for Quantum Learning via Information Theory

Although a concept class may be learnt more efficiently using quantum samples as compared with classical samples in certain scenarios, Arunachalam and de Wolf (JMLR, 2018) proved that quantum learners are asymptotically no more efficient than classical ones in the quantum PAC and Agnostic learning models. They established lower bounds on sample complexity via quantum state identification and Fourier analysis. In this paper, we derive optimal lower bounds for quantum sample complexity in both the PAC and agnostic models via an information-theoretic approach. The proofs are arguably simpler, and the same ideas can potentially be used to derive optimal bounds for other problems in quantum learning theory. We then turn to a quantum analogue of the Coupon Collector problem, a classic problem from probability theory also of importance in the study of PAC learning. Arunachalam, Belovs, Childs, Kothari, Rosmanis, and de Wolf (TQC, 2020) characterized the quantum sample complexity of this problem up to constant factors. First, we show that the information-theoretic approach mentioned above provably does not yield the optimal lower bound. As a by-product, we get a natural ensemble of pure states in arbitrarily high dimensions which are not easily (simultaneously) distinguishable, while the ensemble has close to maximal Holevo information. Second, we discover that the information-theoretic approach yields an asymptotically optimal bound for an approximation variant of the problem. Finally, we derive a sharp lower bound for the Quantum Coupon Collector problem, with the exact leading order term, via the Holevo-Curlander bounds on the distinguishability of an ensemble. All the aspects of the Quantum Coupon Collector problem we study rest on properties of the spectrum of the associated Gram matrix, which may be of independent interest.

Lower bounds for learning quantum states with single-copy measurements

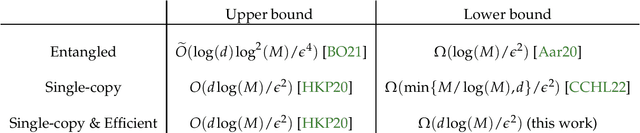
We study the problems of quantum tomography and shadow tomography using measurements performed on individual, identical copies of an unknown $d$-dimensional state. We first revisit a known lower bound due to Haah et al. (2017) on quantum tomography with accuracy $\epsilon$ in trace distance, when the measurements choices are independent of previously observed outcomes (i.e., they are nonadaptive). We give a succinct proof of this result. This leads to stronger lower bounds when the learner uses measurements with a constant number of outcomes. In particular, this rigorously establishes the optimality of the folklore ``Pauli tomography" algorithm in terms of its sample complexity. We also derive novel bounds of $\Omega(r^2 d/\epsilon^2)$ and $\Omega(r^2 d^2/\epsilon^2)$ for learning rank $r$ states using arbitrary and constant-outcome measurements, respectively, in the nonadaptive case. In addition to the sample complexity, a resource of practical significance for learning quantum states is the number of different measurements used by an algorithm. We extend our lower bounds to the case where the learner performs possibly adaptive measurements from a fixed set of $\exp(O(d))$ measurements. This implies in particular that adaptivity does not give us any advantage using single-copy measurements that are efficiently implementable. We also obtain a similar bound in the case where the goal is to predict the expectation values of a given sequence of observables, a task known as shadow tomography. Finally, in the case of adaptive, single-copy measurements implementable with polynomial-size circuits, we prove that a straightforward strategy based on computing sample means of the given observables is optimal.

Online Learning of Quantum States

Suppose we have many copies of an unknown $n$-qubit state $\rho$. We measure some copies of $\rho$ using a known two-outcome measurement $E_{1}$, then other copies using a measurement $E_{2}$, and so on. At each stage $t$, we generate a current hypothesis $\sigma_{t}$ about the state $\rho$, using the outcomes of the previous measurements. We show that it is possible to do this in a way that guarantees that $|\operatorname{Tr}(E_{i} \sigma_{t}) - \operatorname{Tr}(E_{i}\rho) |$, the error in our prediction for the next measurement, is at least $\varepsilon$ at most $\operatorname{O}\!\left(n / \varepsilon^2 \right) $ times. Even in the "non-realizable" setting---where there could be arbitrary noise in the measurement outcomes---we show how to output hypothesis states that do significantly worse than the best possible states at most $\operatorname{O}\!\left(\sqrt {Tn}\right) $ times on the first $T$ measurements. These results generalize a 2007 theorem by Aaronson on the PAC-learnability of quantum states, to the online and regret-minimization settings. We give three different ways to prove our results---using convex optimization, quantum postselection, and sequential fat-shattering dimension---which have different advantages in terms of parameters and portability.