Joint graph learning from Gaussian observations in the presence of hidden nodes

Graph learning problems are typically approached by focusing on learning the topology of a single graph when signals from all nodes are available. However, many contemporary setups involve multiple related networks and, moreover, it is often the case that only a subset of nodes is observed while the rest remain hidden. Motivated by this, we propose a joint graph learning method that takes into account the presence of hidden (latent) variables. Intuitively, the presence of the hidden nodes renders the inference task ill-posed and challenging to solve, so we overcome this detrimental influence by harnessing the similarity of the estimated graphs. To that end, we assume that the observed signals are drawn from a Gaussian Markov random field with latent variables and we carefully model the graph similarity among hidden (latent) nodes. Then, we exploit the structure resulting from the previous considerations to propose a convex optimization problem that solves the joint graph learning task by providing a regularized maximum likelihood estimator. Finally, we compare the proposed algorithm with different baselines and evaluate its performance over synthetic and real-world graphs.

Delay-aware Backpressure Routing Using Graph Neural Networks

We propose a throughput-optimal biased backpressure (BP) algorithm for routing, where the bias is learned through a graph neural network that seeks to minimize end-to-end delay. Classical BP routing provides a simple yet powerful distributed solution for resource allocation in wireless multi-hop networks but has poor delay performance. A low-cost approach to improve this delay performance is to favor shorter paths by incorporating pre-defined biases in the BP computation, such as a bias based on the shortest path (hop) distance to the destination. In this work, we improve upon the widely-used metric of hop distance (and its variants) for the shortest path bias by introducing a bias based on the link duty cycle, which we predict using a graph convolutional neural network. Numerical results show that our approach can improve the delay performance compared to classical BP and existing BP alternatives based on pre-defined bias while being adaptive to interference density. In terms of complexity, our distributed implementation only introduces a one-time overhead (linear in the number of devices in the network) compared to classical BP, and a constant overhead compared to the lowest-complexity existing bias-based BP algorithms.

Graph Filters for Signal Processing and Machine Learning on Graphs

Filters are fundamental in extracting information from data. For time series and image data that reside on Euclidean domains, filters are the crux of many signal processing and machine learning techniques, including convolutional neural networks. Increasingly, modern data also reside on networks and other irregular domains whose structure is better captured by a graph. To process and learn from such data, graph filters account for the structure of the underlying data domain. In this article, we provide a comprehensive overview of graph filters, including the different filtering categories, design strategies for each type, and trade-offs between different types of graph filters. We discuss how to extend graph filters into filter banks and graph neural networks to enhance the representational power; that is, to model a broader variety of signal classes, data patterns, and relationships. We also showcase the fundamental role of graph filters in signal processing and machine learning applications. Our aim is that this article serves the dual purpose of providing a unifying framework for both beginner and experienced researchers, as well as a common understanding that promotes collaborations between signal processing, machine learning, and application domains.

Neural multi-event forecasting on spatio-temporal point processes using probabilistically enriched transformers

Predicting discrete events in time and space has many scientific applications, such as predicting hazardous earthquakes and outbreaks of infectious diseases. History-dependent spatio-temporal Hawkes processes are often used to mathematically model these point events. However, previous approaches have faced numerous challenges, particularly when attempting to forecast one or multiple future events. In this work, we propose a new neural architecture for multi-event forecasting of spatio-temporal point processes, utilizing transformers, augmented with normalizing flows and probabilistic layers. Our network makes batched predictions of complex history-dependent spatio-temporal distributions of future discrete events, achieving state-of-the-art performance on a variety of benchmark datasets including the South California Earthquakes, Citibike, Covid-19, and Hawkes synthetic pinwheel datasets. More generally, we illustrate how our network can be applied to any dataset of discrete events with associated markers, even when no underlying physics is known.

GraphMAD: Graph Mixup for Data Augmentation using Data-Driven Convex Clustering

We develop a novel data-driven nonlinear mixup mechanism for graph data augmentation and present different mixup functions for sample pairs and their labels. Mixup is a data augmentation method to create new training data by linearly interpolating between pairs of data samples and their labels. Mixup of graph data is challenging since the interpolation between graphs of potentially different sizes is an ill-posed operation. Hence, a promising approach for graph mixup is to first project the graphs onto a common latent feature space and then explore linear and nonlinear mixup strategies in this latent space. In this context, we propose to (i) project graphs onto the latent space of continuous random graph models known as graphons, (ii) leverage convex clustering in this latent space to generate nonlinear data-driven mixup functions, and (iii) investigate the use of different mixup functions for labels and data samples. We evaluate our graph data augmentation performance on benchmark datasets and demonstrate that nonlinear data-driven mixup functions can significantly improve graph classification.

Accelerated massive MIMO detector based on annealed underdamped Langevin dynamics

We propose a multiple-input multiple-output (MIMO) detector based on an annealed version of the \emph{underdamped} Langevin (stochastic) dynamic. Our detector achieves state-of-the-art performance in terms of symbol error rate (SER) while keeping the computational complexity in check. Indeed, our method can be easily tuned to strike the right balance between computational complexity and performance as required by the application at hand. This balance is achieved by tuning hyperparameters that control the length of the simulated Langevin dynamic. Through numerical experiments, we demonstrate that our detector yields lower SER than competing approaches (including learning-based ones) with a lower running time compared to a previously proposed \emph{overdamped} Langevin-based MIMO detector.

Joint Network Topology Inference via a Shared Graphon Model

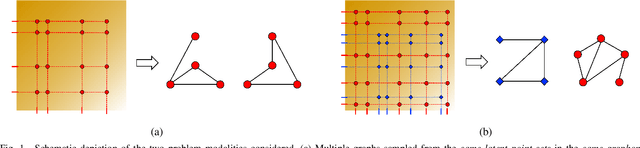
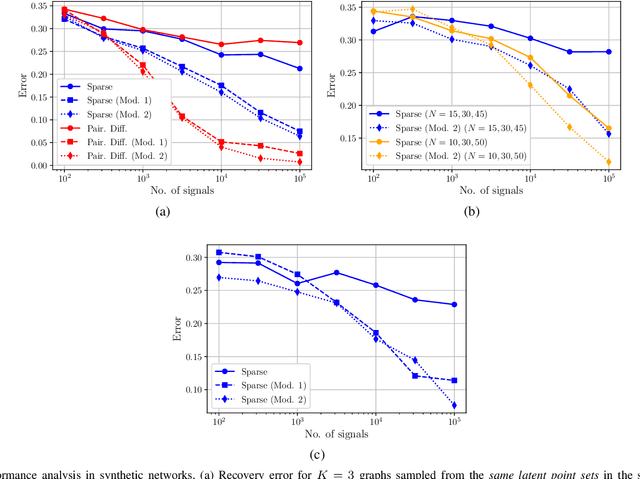
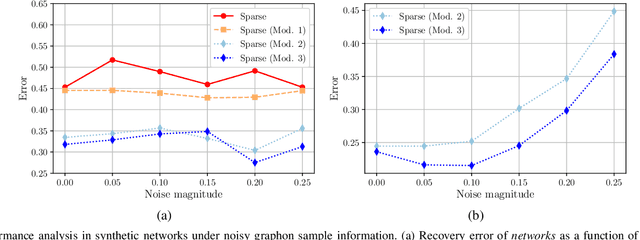
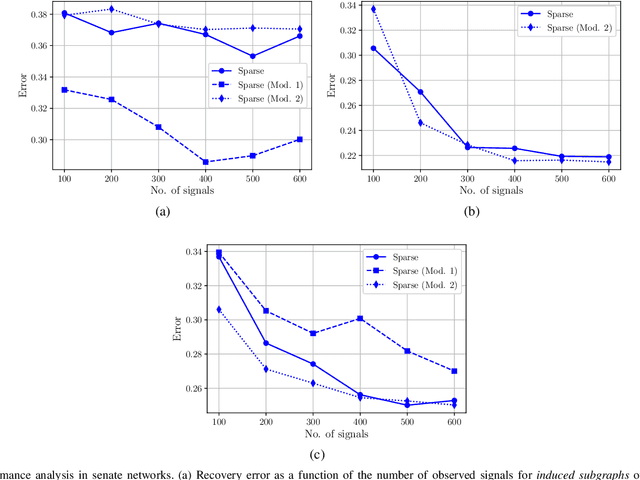
We consider the problem of estimating the topology of multiple networks from nodal observations, where these networks are assumed to be drawn from the same (unknown) random graph model. We adopt a graphon as our random graph model, which is a nonparametric model from which graphs of potentially different sizes can be drawn. The versatility of graphons allows us to tackle the joint inference problem even for the cases where the graphs to be recovered contain different number of nodes and lack precise alignment across the graphs. Our solution is based on combining a maximum likelihood penalty with graphon estimation schemes and can be used to augment existing network inference methods. The proposed joint network and graphon estimation is further enhanced with the introduction of a robust method for noisy graph sampling information. We validate our proposed approach by comparing its performance against competing methods in synthetic and real-world datasets.

Hypergraphs with Edge-Dependent Vertex Weights: p-Laplacians and Spectral Clustering

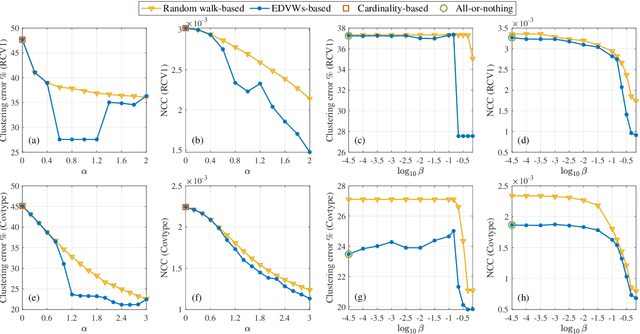
We study p-Laplacians and spectral clustering for a recently proposed hypergraph model that incorporates edge-dependent vertex weights (EDVWs). These weights can reflect different importance of vertices within a hyperedge, thus conferring the hypergraph model higher expressivity and flexibility. By constructing submodular EDVWs-based splitting functions, we convert hypergraphs with EDVWs into submodular hypergraphs for which the spectral theory is better developed. In this way, existing concepts and theorems such as p-Laplacians and Cheeger inequalities proposed under the submodular hypergraph setting can be directly extended to hypergraphs with EDVWs. For submodular hypergraphs with EDVWs-based splitting functions, we propose an efficient algorithm to compute the eigenvector associated with the second smallest eigenvalue of the hypergraph 1-Laplacian. We then utilize this eigenvector to cluster the vertices, achieving higher clustering accuracy than traditional spectral clustering based on the 2-Laplacian. More broadly, the proposed algorithm works for all submodular hypergraphs that are graph reducible. Numerical experiments using real-world data demonstrate the effectiveness of combining spectral clustering based on the 1-Laplacian and EDVWs.

Enhanced graph-learning schemes driven by similar distributions of motifs

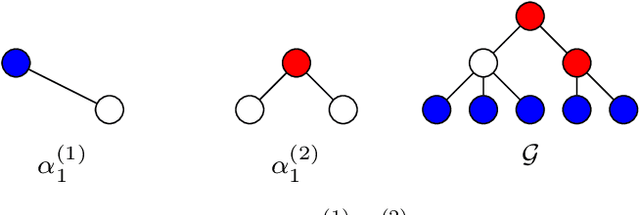
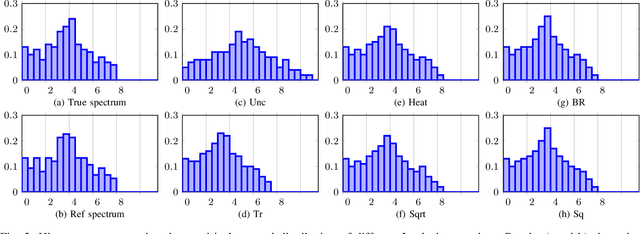
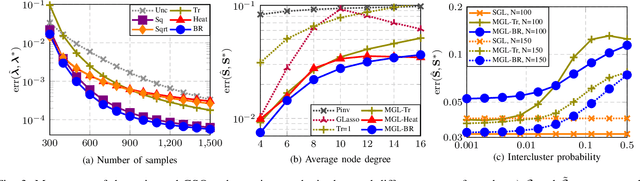
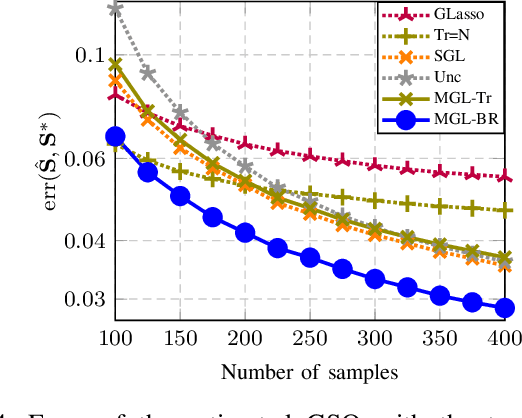
This paper looks at the task of network topology inference, where the goal is to learn an unknown graph from nodal observations. One of the novelties of the approach put forth is the consideration of prior information about the density of motifs of the unknown graph to enhance the inference of classical Gaussian graphical models. Dealing with the density of motifs directly constitutes a challenging combinatorial task. However, we note that if two graphs have similar motif densities, one can show that the expected value of a polynomial applied to their empirical spectral distributions will be similar. Guided by this, we first assume that we have a reference graph that is related to the sought graph (in the sense of having similar motif densities) and then, we exploit this relation by incorporating a similarity constraint and a regularization term in the network topology inference optimization problem. The (non-)convexity of the optimization problem is discussed and a computational efficient alternating majorization-minimization algorithm is designed. We assess the performance of the proposed method through exhaustive numerical experiments where different constraints are considered and compared against popular baselines algorithms on both synthetic and real-world datasets.

Annealed Langevin Dynamics for Massive MIMO Detection

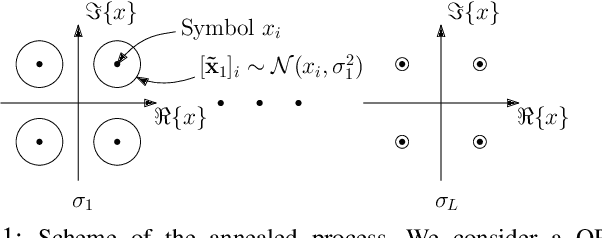
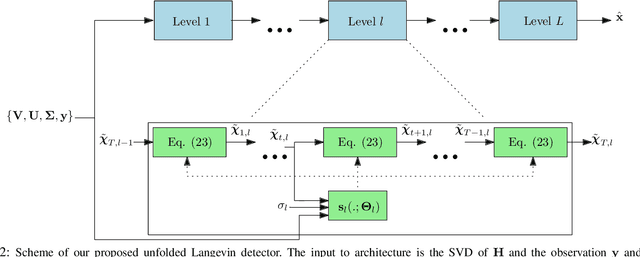
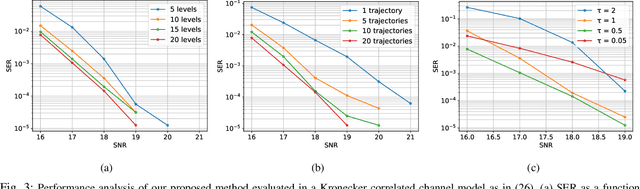
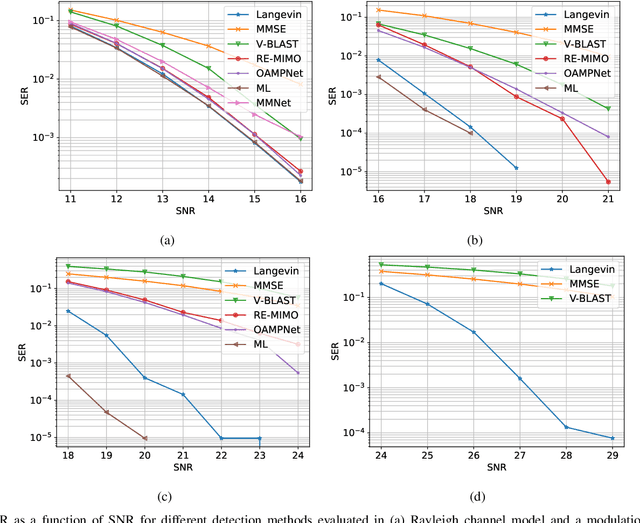
Solving the optimal symbol detection problem in multiple-input multiple-output (MIMO) systems is known to be NP-hard. Hence, the objective of any detector of practical relevance is to get reasonably close to the optimal solution while keeping the computational complexity in check. In this work, we propose a MIMO detector based on an annealed version of Langevin (stochastic) dynamics. More precisely, we define a stochastic dynamical process whose stationary distribution coincides with the posterior distribution of the symbols given our observations. In essence, this allows us to approximate the maximum a posteriori estimator of the transmitted symbols by sampling from the proposed Langevin dynamic. Furthermore, we carefully craft this stochastic dynamic by gradually adding a sequence of noise with decreasing variance to the trajectories, which ensures that the estimated symbols belong to a pre-specified discrete constellation. Based on the proposed MIMO detector, we also design a robust version of the method by unfolding and parameterizing one term -- the score of the likelihood -- by a neural network. Through numerical experiments in both synthetic and real-world data, we show that our proposed detector yields state-of-the-art symbol error rate performance and the robust version becomes noise-variance agnostic.