Unlocking Tokens as Data Points for Generalization Bounds on Larger Language Models

Large language models (LLMs) with billions of parameters excel at predicting the next token in a sequence. Recent work computes non-vacuous compression-based generalization bounds for LLMs, but these bounds are vacuous for large models at the billion-parameter scale. Moreover, these bounds are obtained through restrictive compression techniques, bounding compressed models that generate low-quality text. Additionally, the tightness of these existing bounds depends on the number of IID documents in a training set rather than the much larger number of non-IID constituent tokens, leaving untapped potential for tighter bounds. In this work, we instead use properties of martingales to derive generalization bounds that benefit from the vast number of tokens in LLM training sets. Since a dataset contains far more tokens than documents, our generalization bounds not only tolerate but actually benefit from far less restrictive compression schemes. With Monarch matrices, Kronecker factorizations, and post-training quantization, we achieve non-vacuous generalization bounds for LLMs as large as LLaMA2-70B. Unlike previous approaches, our work achieves the first non-vacuous bounds for models that are deployed in practice and generate high-quality text.

Non-Vacuous Generalization Bounds for Large Language Models

Modern language models can contain billions of parameters, raising the question of whether they can generalize beyond the training data or simply regurgitate their training corpora. We provide the first non-vacuous generalization bounds for pretrained large language models (LLMs), indicating that language models are capable of discovering regularities that generalize to unseen data. In particular, we derive a compression bound that is valid for the unbounded log-likelihood loss using prediction smoothing, and we extend the bound to handle subsampling, accelerating bound computation on massive datasets. To achieve the extreme level of compression required for non-vacuous generalization bounds, we devise SubLoRA, a low-dimensional non-linear parameterization. Using this approach, we find that larger models have better generalization bounds and are more compressible than smaller models.

PAC-Bayes Compression Bounds So Tight That They Can Explain Generalization

While there has been progress in developing non-vacuous generalization bounds for deep neural networks, these bounds tend to be uninformative about why deep learning works. In this paper, we develop a compression approach based on quantizing neural network parameters in a linear subspace, profoundly improving on previous results to provide state-of-the-art generalization bounds on a variety of tasks, including transfer learning. We use these tight bounds to better understand the role of model size, equivariance, and the implicit biases of optimization, for generalization in deep learning. Notably, we find large models can be compressed to a much greater extent than previously known, encapsulating Occam's razor. We also argue for data-independent bounds in explaining generalization.

Bayesian Model Selection, the Marginal Likelihood, and Generalization

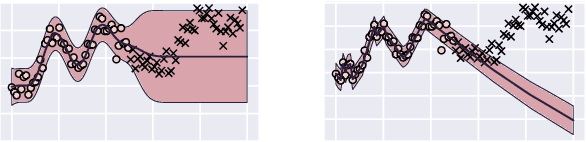
How do we compare between hypotheses that are entirely consistent with observations? The marginal likelihood (aka Bayesian evidence), which represents the probability of generating our observations from a prior, provides a distinctive approach to this foundational question, automatically encoding Occam's razor. Although it has been observed that the marginal likelihood can overfit and is sensitive to prior assumptions, its limitations for hyperparameter learning and discrete model comparison have not been thoroughly investigated. We first revisit the appealing properties of the marginal likelihood for learning constraints and hypothesis testing. We then highlight the conceptual and practical issues in using the marginal likelihood as a proxy for generalization. Namely, we show how marginal likelihood can be negatively correlated with generalization, with implications for neural architecture search, and can lead to both underfitting and overfitting in hyperparameter learning. We provide a partial remedy through a conditional marginal likelihood, which we show is more aligned with generalization, and practically valuable for large-scale hyperparameter learning, such as in deep kernel learning.

Adaptive First- and Second-Order Algorithms for Large-Scale Machine Learning

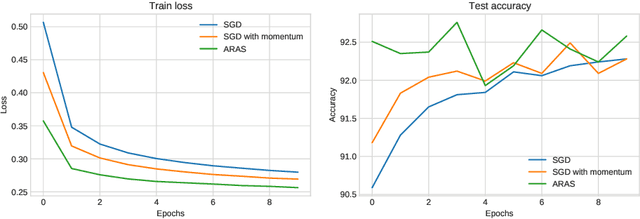
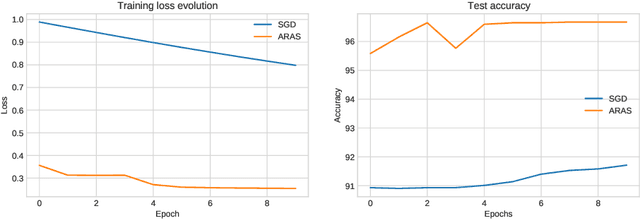
In this paper, we consider both first- and second-order techniques to address continuous optimization problems arising in machine learning. In the first-order case, we propose a framework of transition from deterministic or semi-deterministic to stochastic quadratic regularization methods. We leverage the two-phase nature of stochastic optimization to propose a novel first-order algorithm with adaptive sampling and adaptive step size. In the second-order case, we propose a novel stochastic damped L-BFGS method that improves on previous algorithms in the highly nonconvex context of deep learning. Both algorithms are evaluated on well-known deep learning datasets and exhibit promising performance.

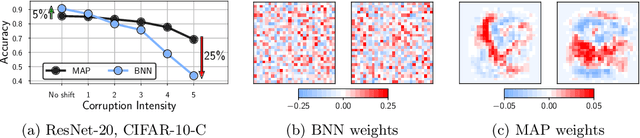
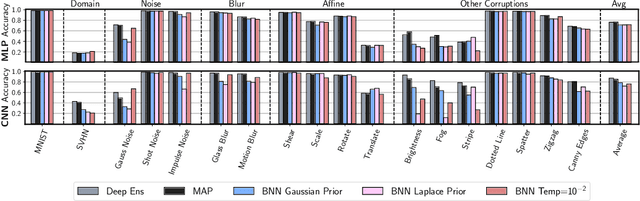
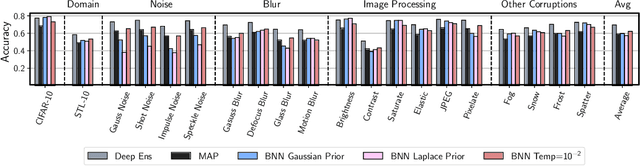
Dangers of Bayesian Model Averaging under Covariate Shift

Approximate Bayesian inference for neural networks is considered a robust alternative to standard training, often providing good performance on out-of-distribution data. However, Bayesian neural networks (BNNs) with high-fidelity approximate inference via full-batch Hamiltonian Monte Carlo achieve poor generalization under covariate shift, even underperforming classical estimation. We explain this surprising result, showing how a Bayesian model average can in fact be problematic under covariate shift, particularly in cases where linear dependencies in the input features cause a lack of posterior contraction. We additionally show why the same issue does not affect many approximate inference procedures, or classical maximum a-posteriori (MAP) training. Finally, we propose novel priors that improve the robustness of BNNs to many sources of covariate shift.

Loss Surface Simplexes for Mode Connecting Volumes and Fast Ensembling

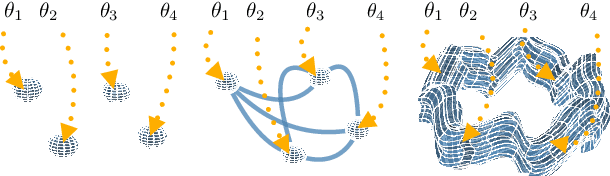
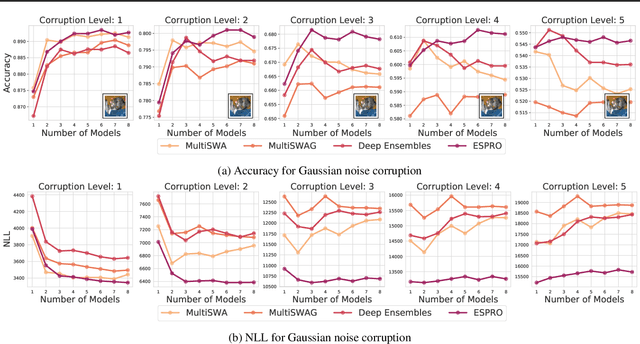
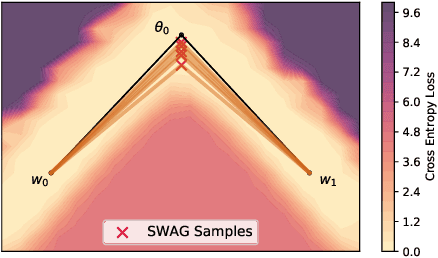
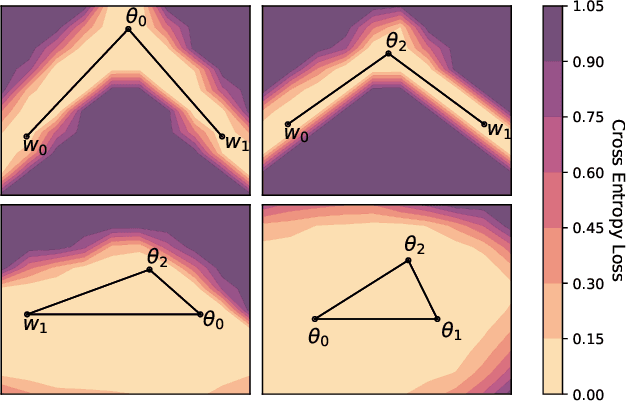
With a better understanding of the loss surfaces for multilayer networks, we can build more robust and accurate training procedures. Recently it was discovered that independently trained SGD solutions can be connected along one-dimensional paths of near-constant training loss. In this paper, we show that there are mode-connecting simplicial complexes that form multi-dimensional manifolds of low loss, connecting many independently trained models. Inspired by this discovery, we show how to efficiently build simplicial complexes for fast ensembling, outperforming independently trained deep ensembles in accuracy, calibration, and robustness to dataset shift. Notably, our approach only requires a few training epochs to discover a low-loss simplex, starting from a pre-trained solution. Code is available at https://github.com/g-benton/loss-surface-simplexes.

Stochastic Damped L-BFGS with Controlled Norm of the Hessian Approximation

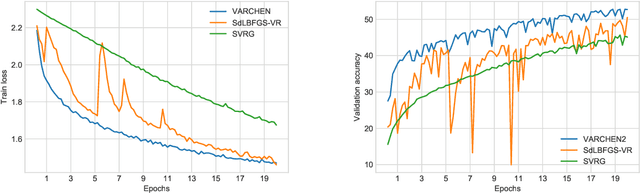
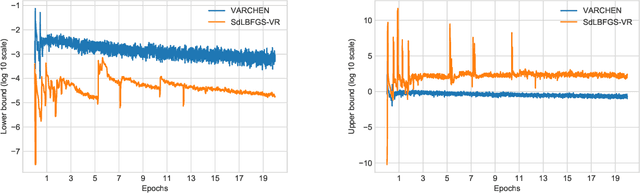
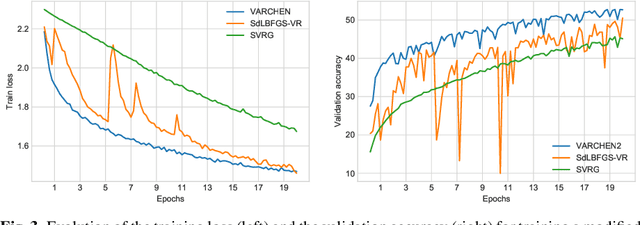
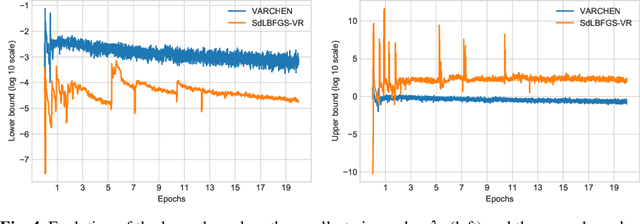
We propose a new stochastic variance-reduced damped L-BFGS algorithm, where we leverage estimates of bounds on the largest and smallest eigenvalues of the Hessian approximation to balance its quality and conditioning. Our algorithm, VARCHEN, draws from previous work that proposed a novel stochastic damped L-BFGS algorithm called SdLBFGS. We establish almost sure convergence to a stationary point and a complexity bound. We empirically demonstrate that VARCHEN is more robust than SdLBFGS-VR and SVRG on a modified DavidNet problem -- a highly nonconvex and ill-conditioned problem that arises in the context of deep learning, and their performance is comparable on a logistic regression problem and a nonconvex support-vector machine problem.