A Proximal Modified Quasi-Newton Method for Nonsmooth Regularized Optimization

We develop R2N, a modified quasi-Newton method for minimizing the sum of a $\mathcal{C}^1$ function $f$ and a lower semi-continuous prox-bounded $h$. Both $f$ and $h$ may be nonconvex. At each iteration, our method computes a step by minimizing the sum of a quadratic model of $f$, a model of $h$, and an adaptive quadratic regularization term. A step may be computed by a variant of the proximal-gradient method. An advantage of R2N over trust-region (TR) methods is that proximal operators do not involve an extra TR indicator. We also develop the variant R2DH, in which the model Hessian is diagonal, which allows us to compute a step without relying on a subproblem solver when $h$ is separable. R2DH can be used as standalone solver, but also as subproblem solver inside R2N. We describe non-monotone variants of both R2N and R2DH. Global convergence of a first-order stationarity measure to zero holds without relying on local Lipschitz continuity of $\nabla f$, while allowing model Hessians to grow unbounded, an assumption particularly relevant to quasi-Newton models. Under Lipschitz-continuity of $\nabla f$, we establish a tight worst-case complexity bound of $O(1 / \epsilon^{2/(1 - p)})$ to bring said measure below $\epsilon > 0$, where $0 \leq p < 1$ controls the growth of model Hessians. The latter must not diverge faster than $|\mathcal{S}_k|^p$, where $\mathcal{S}_k$ is the set of successful iterations up to iteration $k$. When $p = 1$, we establish the tight exponential complexity bound $O(\exp(c \epsilon^{-2}))$ where $c > 0$ is a constant. We describe our Julia implementation and report numerical experience on a basis-pursuit problem, image denoising, minimum-rank matrix completion, and a nonlinear support vector machine. In particular, the minimum-rank problem cannot be solved directly at this time by a TR approach as corresponding proximal operators are not known analytically.

An efficient algorithm for solving linear equality-constrained LQR problems

We present a new algorithm for solving linear-quadratic regulator (LQR) problems with linear equality constraints. This is the first such exact algorithm that is guaranteed to have a runtime that is linear in the number of stages, as well as linear in the number of both state-only constraints as well as mixed state-and-control constraints, without imposing any restrictions on the problem instances. We also show how to easily parallelize this algorithm to run in parallel runtime logarithmic in the number of stages of the problem.

Primal-Dual iLQR

We introduce a new algorithm for solving unconstrained discrete-time optimal control problems. Our method follows a direct multiple shooting approach, and consists of applying the SQP method together with an $\ell_2$ augmented Lagrangian primal-dual merit function. We use the LQR algorithm to efficiently solve the primal component of the Newton-KKT system, and use a dual LQR backward pass to solve its dual component. We also present a new parallel algorithm for solving the dual component of the Newton-KKT system in $O(\log(N))$ parallel time, where $N$ is the number of stages. Combining it with (S\"{a}rkk\"{a} and Garc\'{i}a-Fern\'{a}ndez, 2023), we are able to solve the full Newton-KKT system in $O(\log(N))$ parallel time. The remaining parts of our method have constant parallel time complexity per iteration. Therefore, this paper provides, for the first time, a practical, highly parallelizable (for example, with a GPU) method for solving nonlinear discrete-time optimal control problems. As our algorithm is a specialization of NPSQP (Gill et al. 1992), it inherits its generic properties, including global convergence, fast local convergence, and the lack of need for second order corrections or dimension expansions, improving on existing direct multiple shooting approaches such as acados (Verschueren et al. 2022), ALTRO (Howell et al. 2019), GNMS (Giftthaler et al. 2018), FATROP (Vanroye et al. 2023), and FDDP (Mastalli et al. 2020).

A Stochastic Proximal Method for Nonsmooth Regularized Finite Sum Optimization

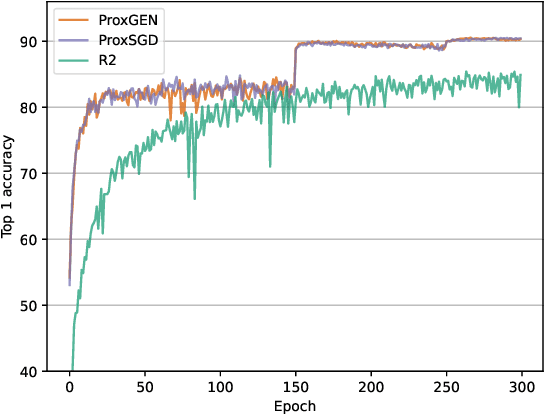
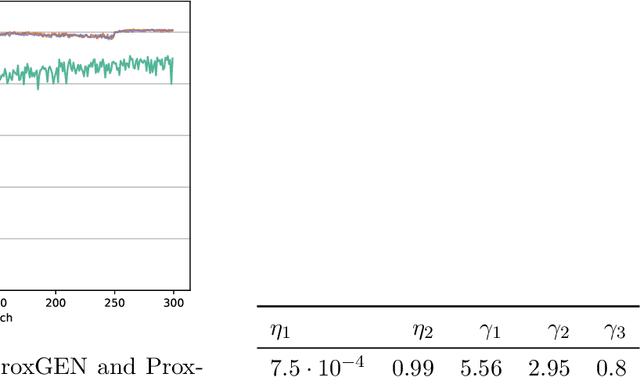
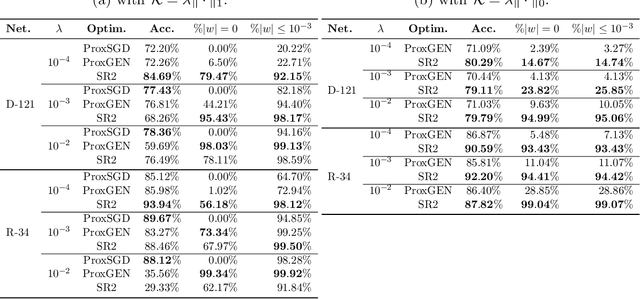
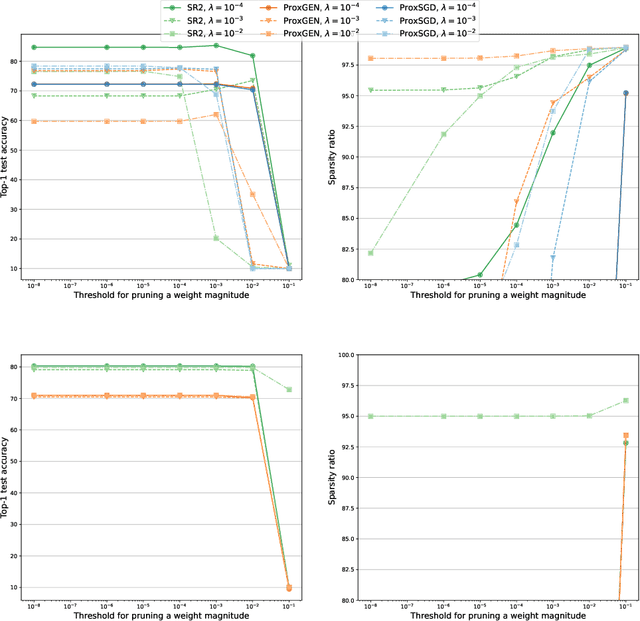
We consider the problem of training a deep neural network with nonsmooth regularization to retrieve a sparse and efficient sub-structure. Our regularizer is only assumed to be lower semi-continuous and prox-bounded. We combine an adaptive quadratic regularization approach with proximal stochastic gradient principles to derive a new solver, called SR2, whose convergence and worst-case complexity are established without knowledge or approximation of the gradient's Lipschitz constant. We formulate a stopping criteria that ensures an appropriate first-order stationarity measure converges to zero under certain conditions. We establish a worst-case iteration complexity of $\mathcal{O}(\epsilon^{-2})$ that matches those of related methods like ProxGEN, where the learning rate is assumed to be related to the Lipschitz constant. Our experiments on network instances trained on CIFAR-10 and CIFAR-100 with $\ell_1$ and $\ell_0$ regularizations show that SR2 consistently achieves higher sparsity and accuracy than related methods such as ProxGEN and ProxSGD.

Adaptive First- and Second-Order Algorithms for Large-Scale Machine Learning

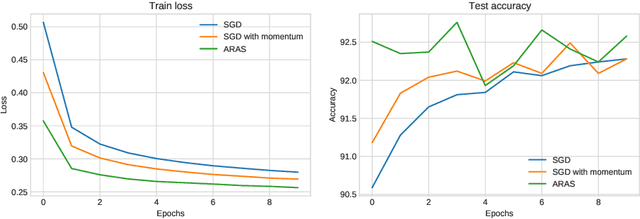
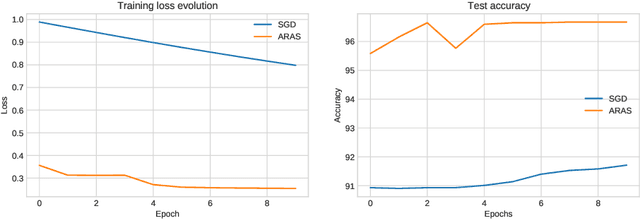
In this paper, we consider both first- and second-order techniques to address continuous optimization problems arising in machine learning. In the first-order case, we propose a framework of transition from deterministic or semi-deterministic to stochastic quadratic regularization methods. We leverage the two-phase nature of stochastic optimization to propose a novel first-order algorithm with adaptive sampling and adaptive step size. In the second-order case, we propose a novel stochastic damped L-BFGS method that improves on previous algorithms in the highly nonconvex context of deep learning. Both algorithms are evaluated on well-known deep learning datasets and exhibit promising performance.

Stochastic Damped L-BFGS with Controlled Norm of the Hessian Approximation

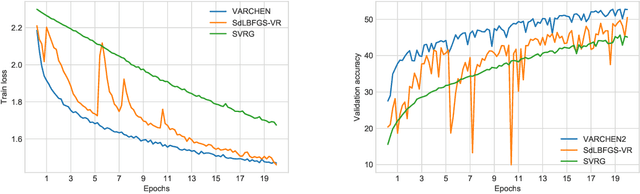
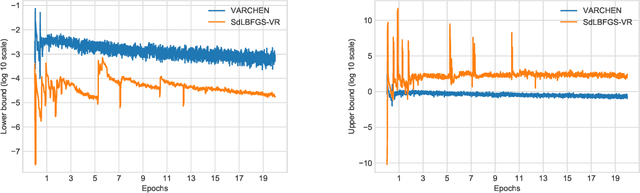
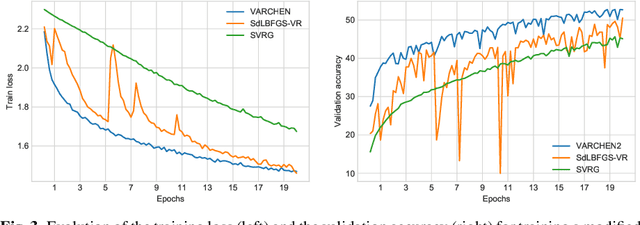
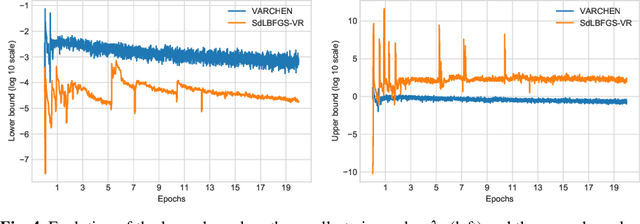
We propose a new stochastic variance-reduced damped L-BFGS algorithm, where we leverage estimates of bounds on the largest and smallest eigenvalues of the Hessian approximation to balance its quality and conditioning. Our algorithm, VARCHEN, draws from previous work that proposed a novel stochastic damped L-BFGS algorithm called SdLBFGS. We establish almost sure convergence to a stationary point and a complexity bound. We empirically demonstrate that VARCHEN is more robust than SdLBFGS-VR and SVRG on a modified DavidNet problem -- a highly nonconvex and ill-conditioned problem that arises in the context of deep learning, and their performance is comparable on a logistic regression problem and a nonconvex support-vector machine problem.