Volatility Based Kernels and Moving Average Means for Accurate Forecasting with Gaussian Processes

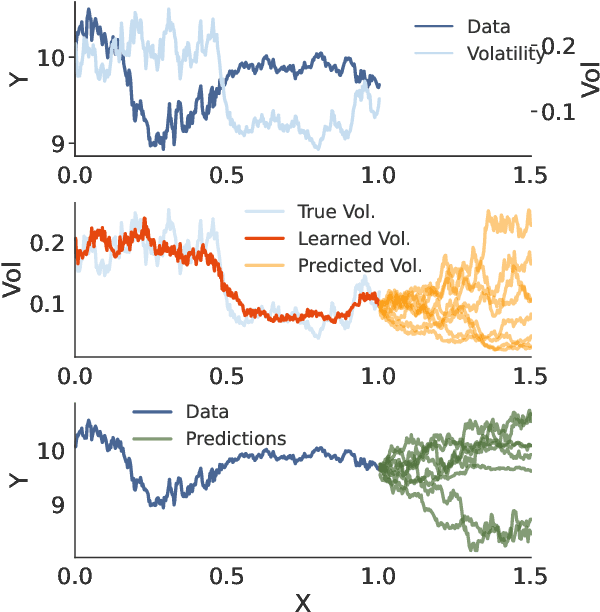
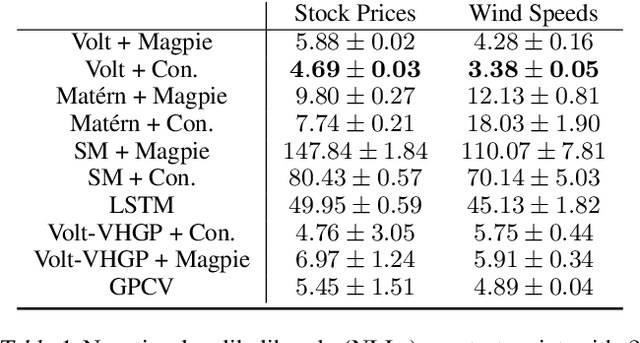
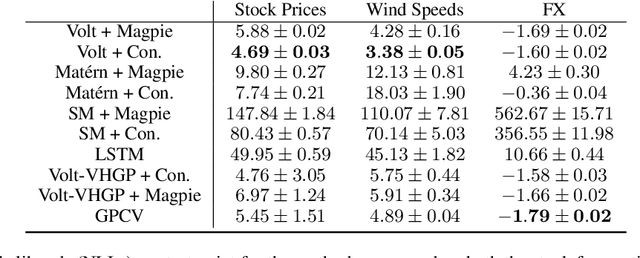
A broad class of stochastic volatility models are defined by systems of stochastic differential equations. While these models have seen widespread success in domains such as finance and statistical climatology, they typically lack an ability to condition on historical data to produce a true posterior distribution. To address this fundamental limitation, we show how to re-cast a class of stochastic volatility models as a hierarchical Gaussian process (GP) model with specialized covariance functions. This GP model retains the inductive biases of the stochastic volatility model while providing the posterior predictive distribution given by GP inference. Within this framework, we take inspiration from well studied domains to introduce a new class of models, Volt and Magpie, that significantly outperform baselines in stock and wind speed forecasting, and naturally extend to the multitask setting.

Bayesian Model Selection, the Marginal Likelihood, and Generalization

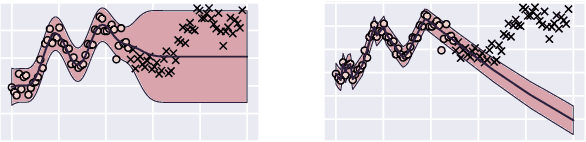
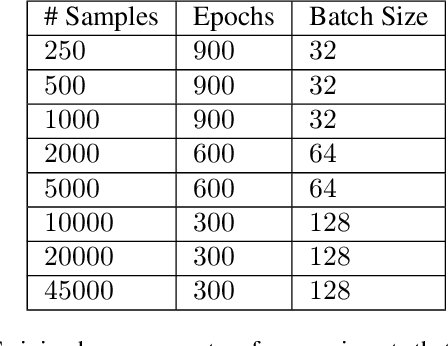
How do we compare between hypotheses that are entirely consistent with observations? The marginal likelihood (aka Bayesian evidence), which represents the probability of generating our observations from a prior, provides a distinctive approach to this foundational question, automatically encoding Occam's razor. Although it has been observed that the marginal likelihood can overfit and is sensitive to prior assumptions, its limitations for hyperparameter learning and discrete model comparison have not been thoroughly investigated. We first revisit the appealing properties of the marginal likelihood for learning constraints and hypothesis testing. We then highlight the conceptual and practical issues in using the marginal likelihood as a proxy for generalization. Namely, we show how marginal likelihood can be negatively correlated with generalization, with implications for neural architecture search, and can lead to both underfitting and overfitting in hyperparameter learning. We provide a partial remedy through a conditional marginal likelihood, which we show is more aligned with generalization, and practically valuable for large-scale hyperparameter learning, such as in deep kernel learning.

Residual Pathway Priors for Soft Equivariance Constraints

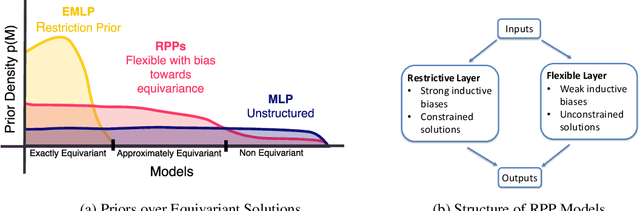
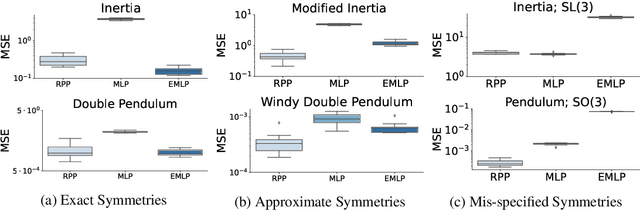
There is often a trade-off between building deep learning systems that are expressive enough to capture the nuances of the reality, and having the right inductive biases for efficient learning. We introduce Residual Pathway Priors (RPPs) as a method for converting hard architectural constraints into soft priors, guiding models towards structured solutions, while retaining the ability to capture additional complexity. Using RPPs, we construct neural network priors with inductive biases for equivariances, but without limiting flexibility. We show that RPPs are resilient to approximate or misspecified symmetries, and are as effective as fully constrained models even when symmetries are exact. We showcase the broad applicability of RPPs with dynamical systems, tabular data, and reinforcement learning. In Mujoco locomotion tasks, where contact forces and directional rewards violate strict equivariance assumptions, the RPP outperforms baseline model-free RL agents, and also improves the learned transition models for model-based RL.

Learning Invariances in Neural Networks

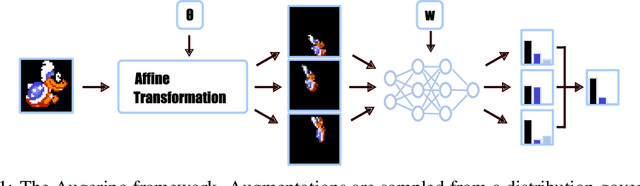
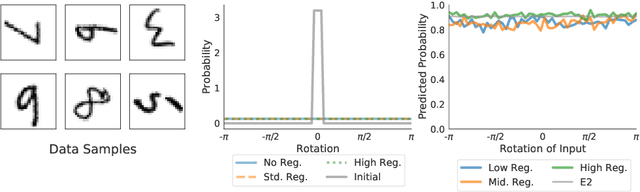
Invariances to translations have imbued convolutional neural networks with powerful generalization properties. However, we often do not know a priori what invariances are present in the data, or to what extent a model should be invariant to a given symmetry group. We show how to \emph{learn} invariances and equivariances by parameterizing a distribution over augmentations and optimizing the training loss simultaneously with respect to the network parameters and augmentation parameters. With this simple procedure we can recover the correct set and extent of invariances on image classification, regression, segmentation, and molecular property prediction from a large space of augmentations, on training data alone.

Rethinking Parameter Counting in Deep Models: Effective Dimensionality Revisited

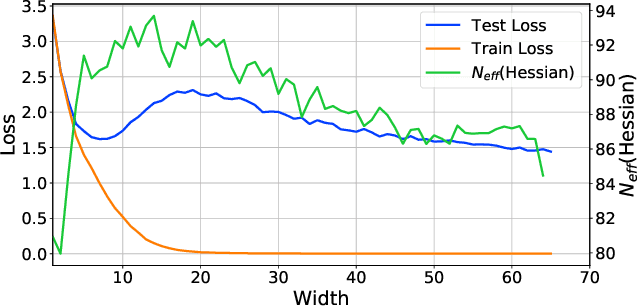
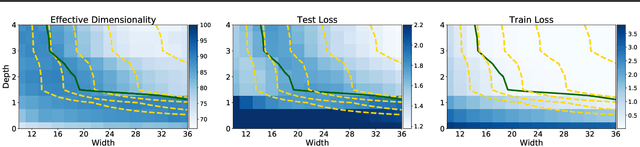
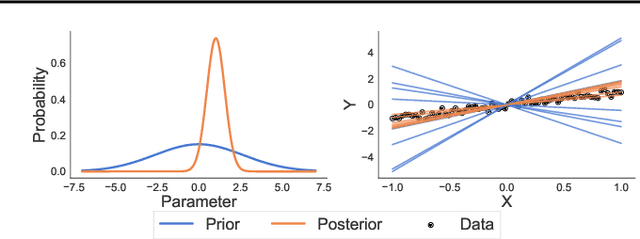
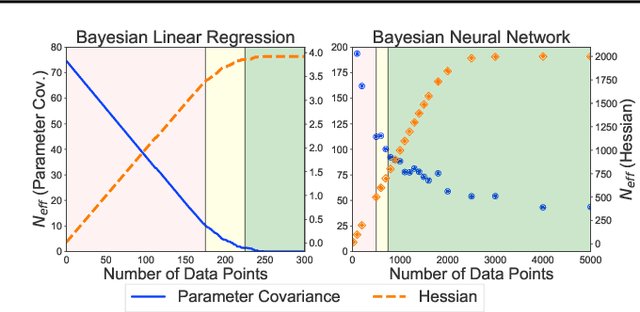
Neural networks appear to have mysterious generalization properties when using parameter counting as a proxy for complexity. Indeed, neural networks often have many more parameters than there are data points, yet still provide good generalization performance. Moreover, when we measure generalization as a function of parameters, we see double descent behaviour, where the test error decreases, increases, and then again decreases. We show that many of these properties become understandable when viewed through the lens of effective dimensionality, which measures the dimensionality of the parameter space determined by the data. We relate effective dimensionality to posterior contraction in Bayesian deep learning, model selection, double descent, and functional diversity in loss surfaces, leading to a richer understanding of the interplay between parameters and functions in deep models.