On the Role of Attention in Prompt-tuning

Prompt-tuning is an emerging strategy to adapt large language models (LLM) to downstream tasks by learning a (soft-)prompt parameter from data. Despite its success in LLMs, there is limited theoretical understanding of the power of prompt-tuning and the role of the attention mechanism in prompting. In this work, we explore prompt-tuning for one-layer attention architectures and study contextual mixture-models where each input token belongs to a context-relevant or -irrelevant set. We isolate the role of prompt-tuning through a self-contained prompt-attention model. Our contributions are as follows: (1) We show that softmax-prompt-attention is provably more expressive than softmax-self-attention and linear-prompt-attention under our contextual data model. (2) We analyze the initial trajectory of gradient descent and show that it learns the prompt and prediction head with near-optimal sample complexity and demonstrate how prompt can provably attend to sparse context-relevant tokens. (3) Assuming a known prompt but an unknown prediction head, we characterize the exact finite sample performance of prompt-attention which reveals the fundamental performance limits and the precise benefit of the context information. We also provide experiments that verify our theoretical insights on real datasets and demonstrate how prompt-tuning enables the model to attend to context-relevant information.

Federated Multi-Sequence Stochastic Approximation with Local Hypergradient Estimation

Stochastic approximation with multiple coupled sequences (MSA) has found broad applications in machine learning as it encompasses a rich class of problems including bilevel optimization (BLO), multi-level compositional optimization (MCO), and reinforcement learning (specifically, actor-critic methods). However, designing provably-efficient federated algorithms for MSA has been an elusive question even for the special case of double sequence approximation (DSA). Towards this goal, we develop FedMSA which is the first federated algorithm for MSA, and establish its near-optimal communication complexity. As core novelties, (i) FedMSA enables the provable estimation of hypergradients in BLO and MCO via local client updates, which has been a notable bottleneck in prior theory, and (ii) our convergence guarantees are sensitive to the heterogeneity-level of the problem. We also incorporate momentum and variance reduction techniques to achieve further acceleration leading to near-optimal rates. Finally, we provide experiments that support our theory and demonstrate the empirical benefits of FedMSA. As an example, FedMSA enables order-of-magnitude savings in communication rounds compared to prior federated BLO schemes.

Dissecting Chain-of-Thought: A Study on Compositional In-Context Learning of MLPs

Chain-of-thought (CoT) is a method that enables language models to handle complex reasoning tasks by decomposing them into simpler steps. Despite its success, the underlying mechanics of CoT are not yet fully understood. In an attempt to shed light on this, our study investigates the impact of CoT on the ability of transformers to in-context learn a simple to study, yet general family of compositional functions: multi-layer perceptrons (MLPs). In this setting, we reveal that the success of CoT can be attributed to breaking down in-context learning of a compositional function into two distinct phases: focusing on data related to each step of the composition and in-context learning the single-step composition function. Through both experimental and theoretical evidence, we demonstrate how CoT significantly reduces the sample complexity of in-context learning (ICL) and facilitates the learning of complex functions that non-CoT methods struggle with. Furthermore, we illustrate how transformers can transition from vanilla in-context learning to mastering a compositional function with CoT by simply incorporating an additional layer that performs the necessary filtering for CoT via the attention mechanism. In addition to these test-time benefits, we highlight how CoT accelerates pretraining by learning shortcuts to represent complex functions and how filtering plays an important role in pretraining. These findings collectively provide insights into the mechanics of CoT, inviting further investigation of its role in complex reasoning tasks.

Learning on Manifolds: Universal Approximations Properties using Geometric Controllability Conditions for Neural ODEs

In numerous robotics and mechanical engineering applications, among others, data is often constrained on smooth manifolds due to the presence of rotational degrees of freedom. Common datadriven and learning-based methods such as neural ordinary differential equations (ODEs), however, typically fail to satisfy these manifold constraints and perform poorly for these applications. To address this shortcoming, in this paper we study a class of neural ordinary differential equations that, by design, leave a given manifold invariant, and characterize their properties by leveraging the controllability properties of control affine systems. In particular, using a result due to Agrachev and Caponigro on approximating diffeomorphisms with flows of feedback control systems, we show that any map that can be represented as the flow of a manifold-constrained dynamical system can also be approximated using the flow of manifold-constrained neural ODE, whenever a certain controllability condition is satisfied. Additionally, we show that this universal approximation property holds when the neural ODE has limited width in each layer, thus leveraging the depth of network instead for approximation. We verify our theoretical findings using numerical experiments on PyTorch for the manifolds S2 and the 3-dimensional orthogonal group SO(3), which are model manifolds for mechanical systems such as spacecrafts and satellites. We also compare the performance of the manifold invariant neural ODE with classical neural ODEs that ignore the manifold invariant properties and show the superiority of our approach in terms of accuracy and sample complexity.

Provable Pathways: Learning Multiple Tasks over Multiple Paths

Constructing useful representations across a large number of tasks is a key requirement for sample-efficient intelligent systems. A traditional idea in multitask learning (MTL) is building a shared representation across tasks which can then be adapted to new tasks by tuning last layers. A desirable refinement of using a shared one-fits-all representation is to construct task-specific representations. To this end, recent PathNet/muNet architectures represent individual tasks as pathways within a larger supernet. The subnetworks induced by pathways can be viewed as task-specific representations that are composition of modules within supernet's computation graph. This work explores the pathways proposal from the lens of statistical learning: We first develop novel generalization bounds for empirical risk minimization problems learning multiple tasks over multiple paths (Multipath MTL). In conjunction, we formalize the benefits of resulting multipath representation when adapting to new downstream tasks. Our bounds are expressed in terms of Gaussian complexity, lead to tangible guarantees for the class of linear representations, and provide novel insights into the quality and benefits of a multipath representation. When computation graph is a tree, Multipath MTL hierarchically clusters the tasks and builds cluster-specific representations. We provide further discussion and experiments for hierarchical MTL and rigorously identify the conditions under which Multipath MTL is provably superior to traditional MTL approaches with shallow supernets.

Stochastic Contextual Bandits with Long Horizon Rewards

The growing interest in complex decision-making and language modeling problems highlights the importance of sample-efficient learning over very long horizons. This work takes a step in this direction by investigating contextual linear bandits where the current reward depends on at most $s$ prior actions and contexts (not necessarily consecutive), up to a time horizon of $h$. In order to avoid polynomial dependence on $h$, we propose new algorithms that leverage sparsity to discover the dependence pattern and arm parameters jointly. We consider both the data-poor ($T<h$) and data-rich ($T\ge h$) regimes, and derive respective regret upper bounds $\tilde O(d\sqrt{sT} +\min\{ q, T\})$ and $\tilde O(\sqrt{sdT})$, with sparsity $s$, feature dimension $d$, total time horizon $T$, and $q$ that is adaptive to the reward dependence pattern. Complementing upper bounds, we also show that learning over a single trajectory brings inherent challenges: While the dependence pattern and arm parameters form a rank-1 matrix, circulant matrices are not isometric over rank-1 manifolds and sample complexity indeed benefits from the sparse reward dependence structure. Our results necessitate a new analysis to address long-range temporal dependencies across data and avoid polynomial dependence on the reward horizon $h$. Specifically, we utilize connections to the restricted isometry property of circulant matrices formed by dependent sub-Gaussian vectors and establish new guarantees that are also of independent interest.

Transformers as Algorithms: Generalization and Implicit Model Selection in In-context Learning

In-context learning (ICL) is a type of prompting where a transformer model operates on a sequence of (input, output) examples and performs inference on-the-fly. This implicit training is in contrast to explicitly tuning the model weights based on examples. In this work, we formalize in-context learning as an algorithm learning problem, treating the transformer model as a learning algorithm that can be specialized via training to implement-at inference-time-another target algorithm. We first explore the statistical aspects of this abstraction through the lens of multitask learning: We obtain generalization bounds for ICL when the input prompt is (1) a sequence of i.i.d. (input, label) pairs or (2) a trajectory arising from a dynamical system. The crux of our analysis is relating the excess risk to the stability of the algorithm implemented by the transformer, which holds under mild assumptions. Secondly, we use our abstraction to show that transformers can act as an adaptive learning algorithm and perform model selection across different hypothesis classes. We provide numerical evaluations that (1) demonstrate transformers can indeed implement near-optimal algorithms on classical regression problems with i.i.d. and dynamic data, (2) identify an inductive bias phenomenon where the transfer risk on unseen tasks is independent of the transformer complexity, and (3) empirically verify our theoretical predictions.

Finite Sample Identification of Bilinear Dynamical Systems

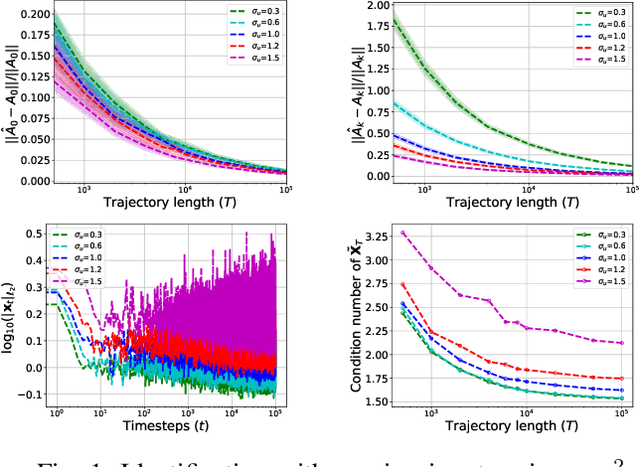
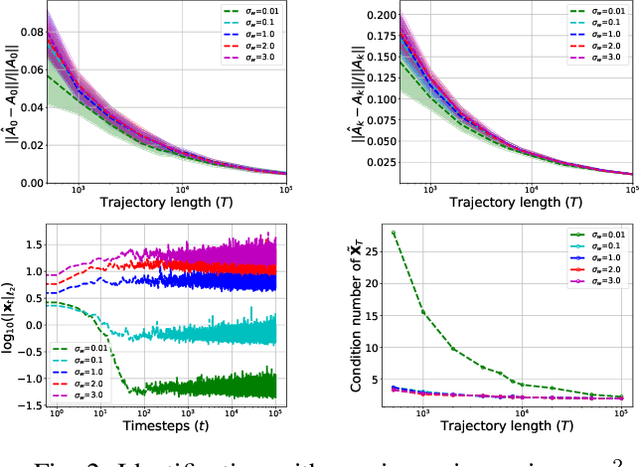
Bilinear dynamical systems are ubiquitous in many different domains and they can also be used to approximate more general control-affine systems. This motivates the problem of learning bilinear systems from a single trajectory of the system's states and inputs. Under a mild marginal mean-square stability assumption, we identify how much data is needed to estimate the unknown bilinear system up to a desired accuracy with high probability. Our sample complexity and statistical error rates are optimal in terms of the trajectory length, the dimensionality of the system and the input size. Our proof technique relies on an application of martingale small-ball condition. This enables us to correctly capture the properties of the problem, specifically our error rates do not deteriorate with increasing instability. Finally, we show that numerical experiments are well-aligned with our theoretical results.

Representation Learning for Context-Dependent Decision-Making

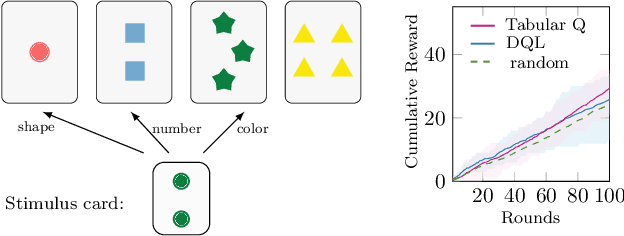
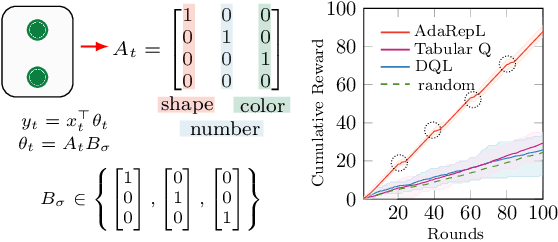
Humans are capable of adjusting to changing environments flexibly and quickly. Empirical evidence has revealed that representation learning plays a crucial role in endowing humans with such a capability. Inspired by this observation, we study representation learning in the sequential decision-making scenario with contextual changes. We propose an online algorithm that is able to learn and transfer context-dependent representations and show that it significantly outperforms the existing ones that do not learn representations adaptively. As a case study, we apply our algorithm to the Wisconsin Card Sorting Task, a well-established test for the mental flexibility of humans in sequential decision-making. By comparing our algorithm with the standard Q-learning and Deep-Q learning algorithms, we demonstrate the benefits of adaptive representation learning.

FEDNEST: Federated Bilevel, Minimax, and Compositional Optimization

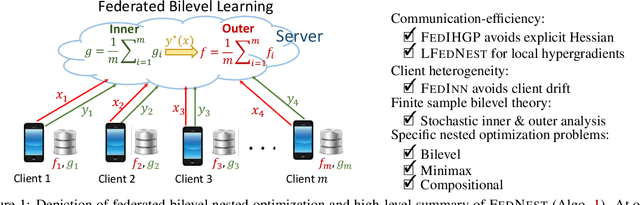
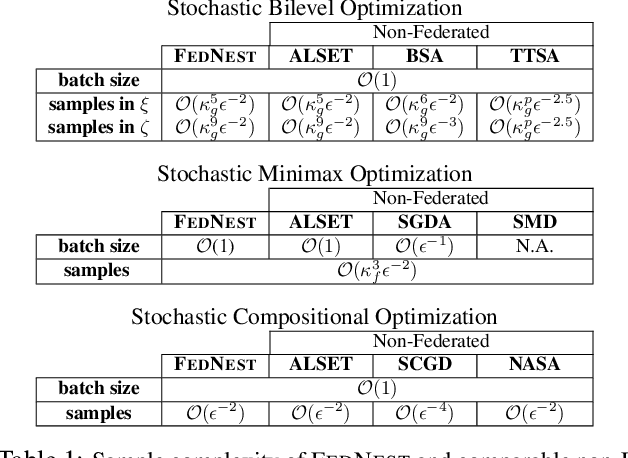
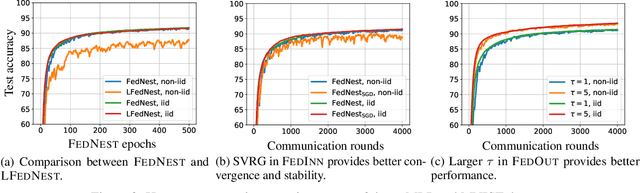
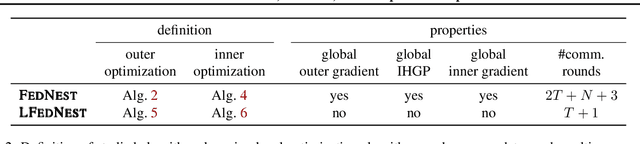
Standard federated optimization methods successfully apply to stochastic problems with single-level structure. However, many contemporary ML problems -- including adversarial robustness, hyperparameter tuning, and actor-critic -- fall under nested bilevel programming that subsumes minimax and compositional optimization. In this work, we propose FEDNEST: A federated alternating stochastic gradient method to address general nested problems. We establish provable convergence rates for FEDNEST in the presence of heterogeneous data and introduce variations for bilevel, minimax, and compositional optimization. FEDNEST introduces multiple innovations including federated hypergradient computation and variance reduction to address inner-level heterogeneity. We complement our theory with experiments on hyperparameter \& hyper-representation learning and minimax optimization that demonstrate the benefits of our method in practice. Code is available at https://github.com/mc-nya/FedNest.