Disentanglement in T-space for Faster and Distributed Training of Diffusion Models with Fewer Latent-states

We challenge a fundamental assumption of diffusion models, namely, that a large number of latent-states or time-steps is required for training so that the reverse generative process is close to a Gaussian. We first show that with careful selection of a noise schedule, diffusion models trained over a small number of latent states (i.e. $T \sim 32$) match the performance of models trained over a much large number of latent states ($T \sim 1,000$). Second, we push this limit (on the minimum number of latent states required) to a single latent-state, which we refer to as complete disentanglement in T-space. We show that high quality samples can be easily generated by the disentangled model obtained by combining several independently trained single latent-state models. We provide extensive experiments to show that the proposed disentangled model provides 4-6$\times$ faster convergence measured across a variety of metrics on two different datasets.

Uncertainty Informed Optimal Resource Allocation with Gaussian Process based Bayesian Inference

We focus on the problem of uncertainty informed allocation of medical resources (vaccines) to heterogeneous populations for managing epidemic spread. We tackle two related questions: (1) For a compartmental ordinary differential equation (ODE) model of epidemic spread, how can we estimate and integrate parameter uncertainty into resource allocation decisions? (2) How can we computationally handle both nonlinear ODE constraints and parameter uncertainties for a generic stochastic optimization problem for resource allocation? To the best of our knowledge current literature does not fully resolve these questions. Here, we develop a data-driven approach to represent parameter uncertainty accurately and tractably in a novel stochastic optimization problem formulation. We first generate a tractable scenario set by estimating the distribution on ODE model parameters using Bayesian inference with Gaussian processes. Next, we develop a parallelized solution algorithm that accounts for scenario-dependent nonlinear ODE constraints. Our scenario-set generation procedure and solution approach are flexible in that they can handle any compartmental epidemiological ODE model. Our computational experiments on two different non-linear ODE models (SEIR and SEPIHR) indicate that accounting for uncertainty in key epidemiological parameters can improve the efficacy of time-critical allocation decisions by 4-8%. This improvement can be attributed to data-driven and optimal (strategic) nature of vaccine allocations, especially in the early stages of the epidemic when the allocation strategy can crucially impact the long-term trajectory of the disease.

Bayesian regularization of empirical MDPs

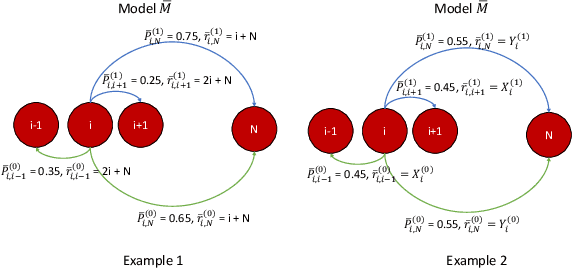
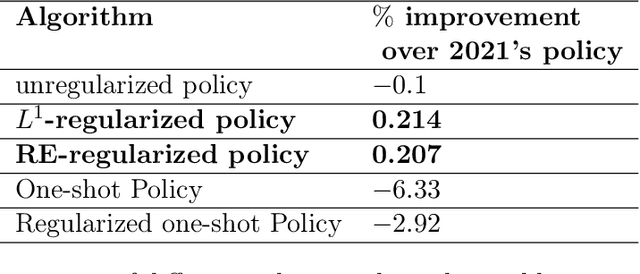
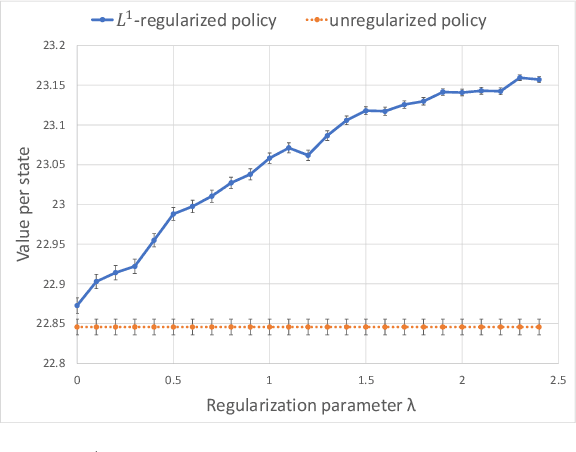
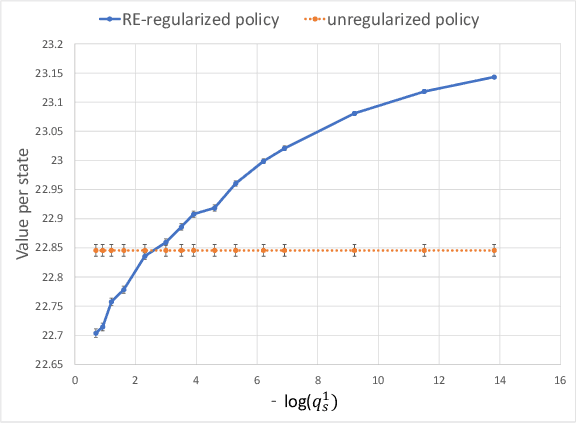
In most applications of model-based Markov decision processes, the parameters for the unknown underlying model are often estimated from the empirical data. Due to noise, the policy learnedfrom the estimated model is often far from the optimal policy of the underlying model. When applied to the environment of the underlying model, the learned policy results in suboptimal performance, thus calling for solutions with better generalization performance. In this work we take a Bayesian perspective and regularize the objective function of the Markov decision process with prior information in order to obtain more robust policies. Two approaches are proposed, one based on $L^1$ regularization and the other on relative entropic regularization. We evaluate our proposed algorithms on synthetic simulations and on real-world search logs of a large scale online shopping store. Our results demonstrate the robustness of regularized MDP policies against the noise present in the models.

Quasi-Newton policy gradient algorithms

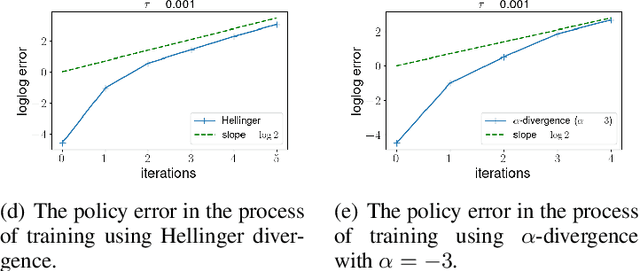
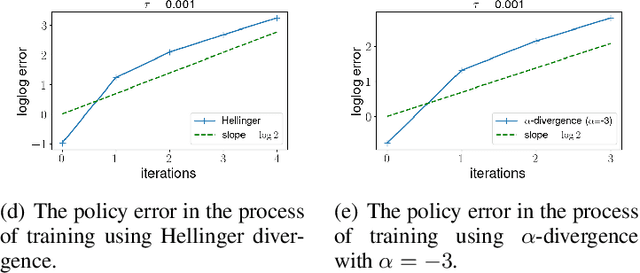
Policy gradient algorithms have been widely applied to reinforcement learning (RL) problems in recent years. Regularization with various entropy functions is often used to encourage exploration and improve stability. In this paper, we propose a quasi-Newton method for the policy gradient algorithm with entropy regularization. In the case of Shannon entropy, the resulting algorithm reproduces the natural policy gradient (NPG) algorithm. For other entropy functions, this method results in brand new policy gradient algorithms. We provide a simple proof that all these algorithms enjoy the Newton-type quadratic convergence near the optimal policy. Using synthetic and industrial-scale examples, we demonstrate that the proposed quasi-Newton method typically converges in single-digit iterations, often orders of magnitude faster than other state-of-the-art algorithms.

Best-Arm Identification in Correlated Multi-Armed Bandits

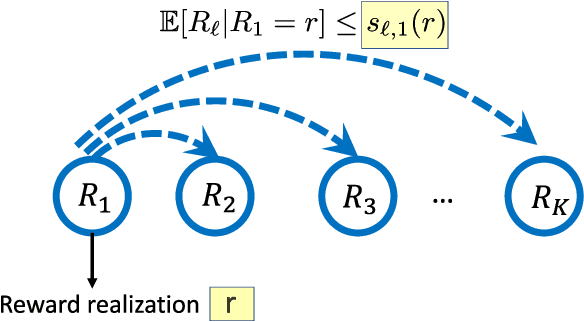
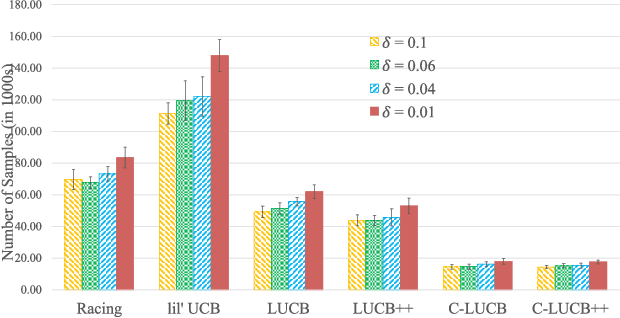
In this paper we consider the problem of best-arm identification in multi-armed bandits in the fixed confidence setting, where the goal is to identify, with probability $1-\delta$ for some $\delta>0$, the arm with the highest mean reward in minimum possible samples from the set of arms $\mathcal{K}$. Most existing best-arm identification algorithms and analyses operate under the assumption that the rewards corresponding to different arms are independent of each other. We propose a novel correlated bandit framework that captures domain knowledge about correlation between arms in the form of upper bounds on expected conditional reward of an arm, given a reward realization from another arm. Our proposed algorithm C-LUCB, which generalizes the LUCB algorithm utilizes this partial knowledge of correlations to sharply reduce the sample complexity of best-arm identification. More interestingly, we show that the total samples obtained by C-LUCB are of the form $\mathcal{O}\left(\sum_{k \in \mathcal{C}} \log\left(\frac{1}{\delta}\right)\right)$ as opposed to the typical $\mathcal{O}\left(\sum_{k \in \mathcal{K}} \log\left(\frac{1}{\delta}\right)\right)$ samples required in the independent reward setting. The improvement comes, as the $\mathcal{O}(\log(1/\delta))$ term is summed only for the set of competitive arms $\mathcal{C}$, which is a subset of the original set of arms $\mathcal{K}$. The size of the set $\mathcal{C}$, depending on the problem setting, can be as small as $2$, and hence using C-LUCB in the correlated bandits setting can lead to significant performance improvements. Our theoretical findings are supported by experiments on the Movielens and Goodreads recommendation datasets.

Bandit-based Communication-Efficient Client Selection Strategies for Federated Learning

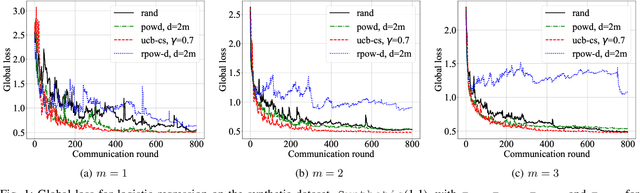
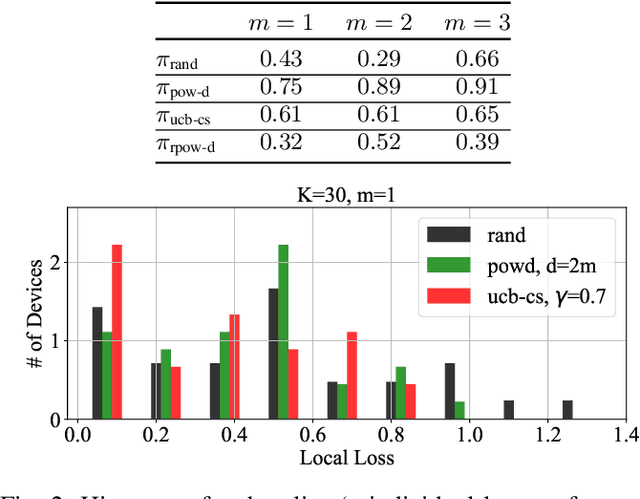
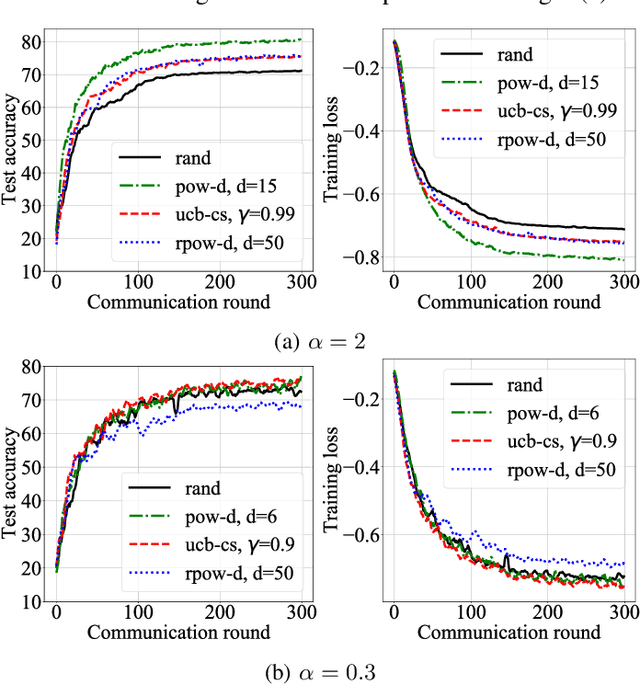
Due to communication constraints and intermittent client availability in federated learning, only a subset of clients can participate in each training round. While most prior works assume uniform and unbiased client selection, recent work on biased client selection has shown that selecting clients with higher local losses can improve error convergence speed. However, previously proposed biased selection strategies either require additional communication cost for evaluating the exact local loss or utilize stale local loss, which can even make the model diverge. In this paper, we present a bandit-based communication-efficient client selection strategy UCB-CS that achieves faster convergence with lower communication overhead. We also demonstrate how client selection can be used to improve fairness.

Integer Programming-based Error-Correcting Output Code Design for Robust Classification

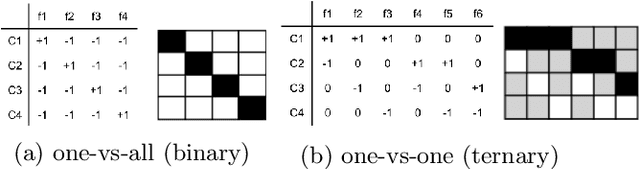
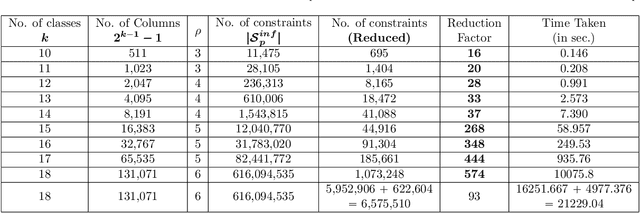
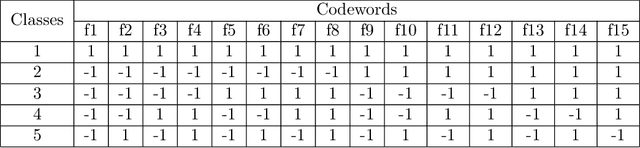
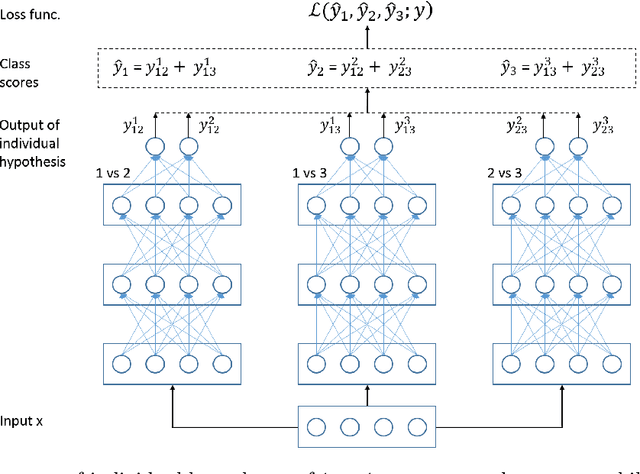
Error-Correcting Output Codes (ECOCs) offer a principled approach for combining simple binary classifiers into multiclass classifiers. In this paper, we investigate the problem of designing optimal ECOCs to achieve both nominal and adversarial accuracy using Support Vector Machines (SVMs) and binary deep learning models. In contrast to previous literature, we present an Integer Programming (IP) formulation to design minimal codebooks with desirable error correcting properties. Our work leverages the advances in IP solvers to generate codebooks with optimality guarantees. To achieve tractability, we exploit the underlying graph-theoretic structure of the constraint set in our IP formulation. This enables us to use edge clique covers to substantially reduce the constraint set. Our codebooks achieve a high nominal accuracy relative to standard codebooks (e.g., one-vs-all, one-vs-one, and dense/sparse codes). We also estimate the adversarial accuracy of our ECOC-based classifiers in a white-box setting. Our IP-generated codebooks provide non-trivial robustness to adversarial perturbations even without any adversarial training.

Multi-Armed Bandits with Correlated Arms

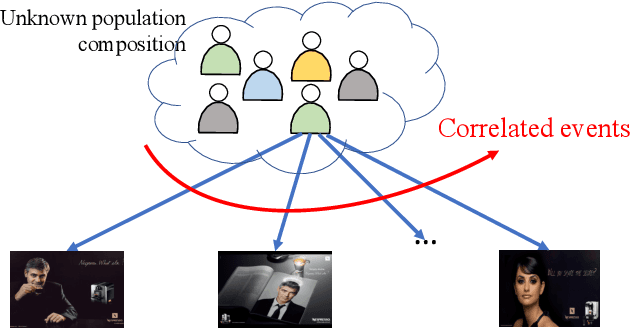
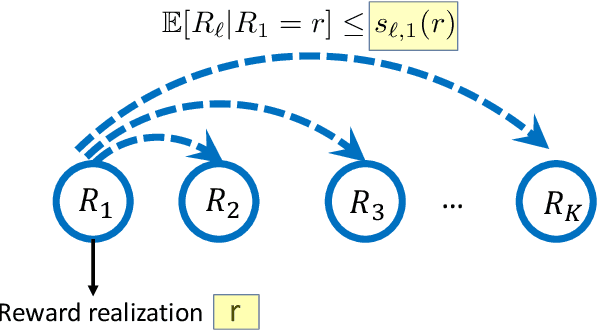
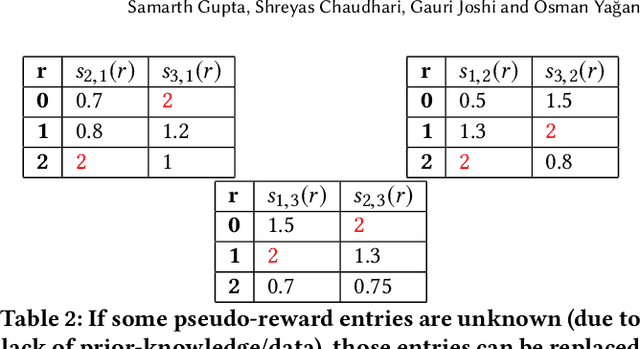
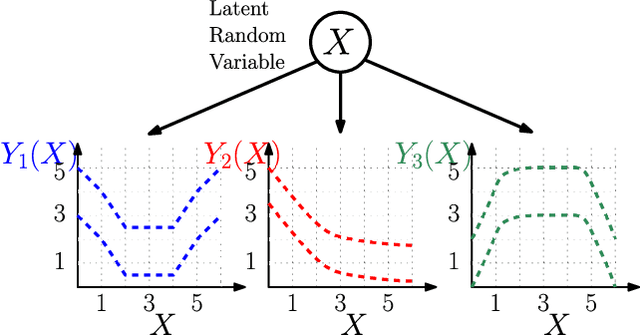
We consider a multi-armed bandit framework where the rewards obtained by pulling different arms are correlated. The correlation information is captured in terms of \textit{pseudo-rewards}, which are bounds on the rewards on the other arm given a reward realization and can capture many general correlation structures. We leverage these pseudo-rewards to design a novel approach that extends any classical bandit algorithm to the correlated multi-armed bandit setting studied in the framework. In each round, our proposed C-Bandit algorithm identifies some arms as empirically non-competitive, and avoids exploring them for that round. Through a unified regret analysis of the proposed C-Bandit algorithm, we show that C-UCB and C-TS (the correlated bandit versions of Upper-confidence-bound and Thompson sampling) pull certain arms called non-competitive arms, only O(1) times. As a result, we effectively reduce a $K$-armed bandit problem to a $C+1$-armed bandit problem, where $C$ is the number of competitive arms, as only $C$ sub-optimal arms are pulled O(log T) times. In many practical scenarios, $C$ can be zero due to which our proposed C-Bandit algorithms achieve bounded regret. In the special case where rewards are correlated through a latent random variable $X$, we give a regret lower bound that shows that bounded regret is possible only when $C = 0$. In addition to simulations, we validate the proposed algorithms via experiments on two real-world recommendation datasets, movielens and goodreads, and show that C-UCB and C-TS significantly outperform classical bandit algorithms.

Exploiting Correlation in Finite-Armed Structured Bandits

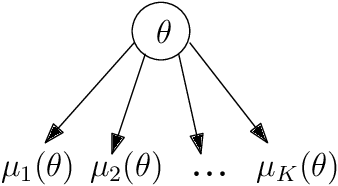
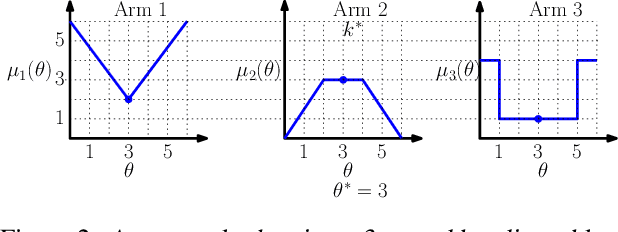
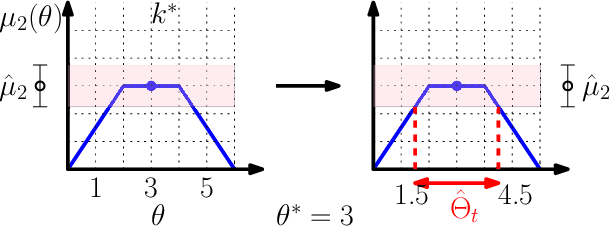
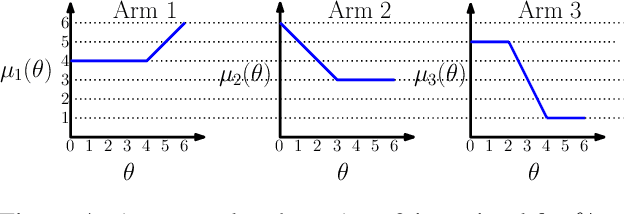
We consider a correlated multi-armed bandit problem in which rewards of arms are correlated through a hidden parameter. Our approach exploits the correlation among arms to identify some arms as sub-optimal and pulls them only $\mathcal{O}(1)$ times. This results in significant reduction in cumulative regret, and in fact our algorithm achieves bounded (i.e., $\mathcal{O}(1)$) regret whenever possible; explicit conditions needed for bounded regret to be possible are also provided by analyzing regret lower bounds. We propose several variants of our approach that generalize classical bandit algorithms such as UCB, Thompson sampling, KL-UCB to the structured bandit setting, and empirically demonstrate their superiority via simulations.

Correlated Multi-armed Bandits with a Latent Random Source

We consider a novel multi-armed bandit framework where the rewards obtained by pulling the arms are functions of a common latent random variable. The correlation between arms due to the common random source can be used to design a generalized upper-confidence-bound (UCB) algorithm that identifies certain arms as $non-competitive$, and avoids exploring them. As a result, we reduce a $K$-armed bandit problem to a $C+1$-armed problem, where $C+1$ includes the best arm and $C$ $competitive$ arms. Our regret analysis shows that the competitive arms need to be pulled $\mathcal{O}(\log T)$ times, while the non-competitive arms are pulled only $\mathcal{O}(1)$ times. As a result, there are regimes where our algorithm achieves a $\mathcal{O}(1)$ regret as opposed to the typical logarithmic regret scaling of multi-armed bandit algorithms. We also evaluate lower bounds on the expected regret and prove that our correlated-UCB algorithm is order-wise optimal.