On the Convergence and Stability of Upside-Down Reinforcement Learning, Goal-Conditioned Supervised Learning, and Online Decision Transformers

This article provides a rigorous analysis of convergence and stability of Episodic Upside-Down Reinforcement Learning, Goal-Conditioned Supervised Learning and Online Decision Transformers. These algorithms performed competitively across various benchmarks, from games to robotic tasks, but their theoretical understanding is limited to specific environmental conditions. This work initiates a theoretical foundation for algorithms that build on the broad paradigm of approaching reinforcement learning through supervised learning or sequence modeling. At the core of this investigation lies the analysis of conditions on the underlying environment, under which the algorithms can identify optimal solutions. We also assess whether emerging solutions remain stable in situations where the environment is subject to tiny levels of noise. Specifically, we study the continuity and asymptotic convergence of command-conditioned policies, values and the goal-reaching objective depending on the transition kernel of the underlying Markov Decision Process. We demonstrate that near-optimal behavior is achieved if the transition kernel is located in a sufficiently small neighborhood of a deterministic kernel. The mentioned quantities are continuous (with respect to a specific topology) at deterministic kernels, both asymptotically and after a finite number of learning cycles. The developed methods allow us to present the first explicit estimates on the convergence and stability of policies and values in terms of the underlying transition kernels. On the theoretical side we introduce a number of new concepts to reinforcement learning, like working in segment spaces, studying continuity in quotient topologies and the application of the fixed-point theory of dynamical systems. The theoretical study is accompanied by a detailed investigation of example environments and numerical experiments.

Bayesian Flow Networks

This paper introduces Bayesian Flow Networks (BFNs), a new class of generative model in which the parameters of a set of independent distributions are modified with Bayesian inference in the light of noisy data samples, then passed as input to a neural network that outputs a second, interdependent distribution. Starting from a simple prior and iteratively updating the two distributions yields a generative procedure similar to the reverse process of diffusion models; however it is conceptually simpler in that no forward process is required. Discrete and continuous-time loss functions are derived for continuous, discretised and discrete data, along with sample generation procedures. Notably, the network inputs for discrete data lie on the probability simplex, and are therefore natively differentiable, paving the way for gradient-based sample guidance and few-step generation in discrete domains such as language modelling. The loss function directly optimises data compression and places no restrictions on the network architecture. In our experiments BFNs achieve competitive log-likelihoods for image modelling on dynamically binarized MNIST and CIFAR-10, and outperform all known discrete diffusion models on the text8 character-level language modelling task.

Universal Smoothed Score Functions for Generative Modeling

We consider the problem of generative modeling based on smoothing an unknown density of interest in $\mathbb{R}^d$ using factorial kernels with $M$ independent Gaussian channels with equal noise levels introduced by Saremi and Srivastava (2022). First, we fully characterize the time complexity of learning the resulting smoothed density in $\mathbb{R}^{Md}$, called M-density, by deriving a universal form for its parametrization in which the score function is by construction permutation equivariant. Next, we study the time complexity of sampling an M-density by analyzing its condition number for Gaussian distributions. This spectral analysis gives a geometric insight on the "shape" of M-densities as one increases $M$. Finally, we present results on the sample quality in this class of generative models on the CIFAR-10 dataset where we report Fr\'echet inception distances (14.15), notably obtained with a single noise level on long-run fast-mixing MCMC chains.

EvoTorch: Scalable Evolutionary Computation in Python

Evolutionary computation is an important component within various fields such as artificial intelligence research, reinforcement learning, robotics, industrial automation and/or optimization, engineering design, etc. Considering the increasing computational demands and the dimensionalities of modern optimization problems, the requirement for scalable, re-usable, and practical evolutionary algorithm implementations has been growing. To address this requirement, we present EvoTorch: an evolutionary computation library designed to work with high-dimensional optimization problems, with GPU support and with high parallelization capabilities. EvoTorch is based on and seamlessly works with the PyTorch library, and therefore, allows the users to define their optimization problems using a well-known API.

Upside-Down Reinforcement Learning Can Diverge in Stochastic Environments With Episodic Resets

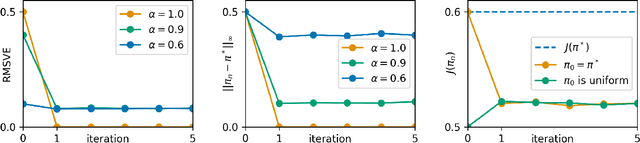
Upside-Down Reinforcement Learning (UDRL) is an approach for solving RL problems that does not require value functions and uses only supervised learning, where the targets for given inputs in a dataset do not change over time. Ghosh et al. proved that Goal-Conditional Supervised Learning (GCSL) -- which can be viewed as a simplified version of UDRL -- optimizes a lower bound on goal-reaching performance. This raises expectations that such algorithms may enjoy guaranteed convergence to the optimal policy in arbitrary environments, similar to certain well-known traditional RL algorithms. Here we show that for a specific episodic UDRL algorithm (eUDRL, including GCSL), this is not the case, and give the causes of this limitation. To do so, we first introduce a helpful rewrite of eUDRL as a recursive policy update. This formulation helps to disprove its convergence to the optimal policy for a wide class of stochastic environments. Finally, we provide a concrete example of a very simple environment where eUDRL diverges. Since the primary aim of this paper is to present a negative result, and the best counterexamples are the simplest ones, we restrict all discussions to finite (discrete) environments, ignoring issues of function approximation and limited sample size.

Learning Relative Return Policies With Upside-Down Reinforcement Learning

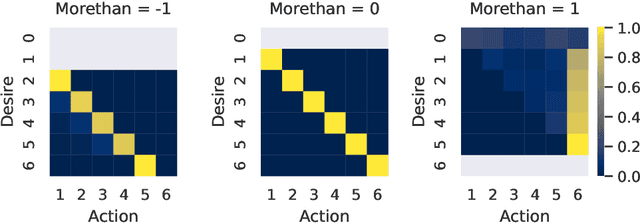
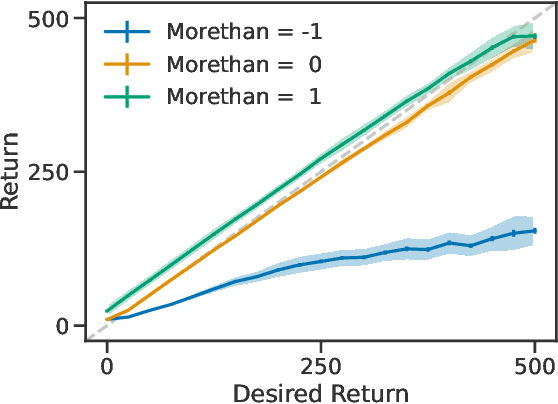
Lately, there has been a resurgence of interest in using supervised learning to solve reinforcement learning problems. Recent work in this area has largely focused on learning command-conditioned policies. We investigate the potential of one such method -- upside-down reinforcement learning -- to work with commands that specify a desired relationship between some scalar value and the observed return. We show that upside-down reinforcement learning can learn to carry out such commands online in a tabular bandit setting and in CartPole with non-linear function approximation. By doing so, we demonstrate the power of this family of methods and open the way for their practical use under more complicated command structures.

Multimeasurement Generative Models

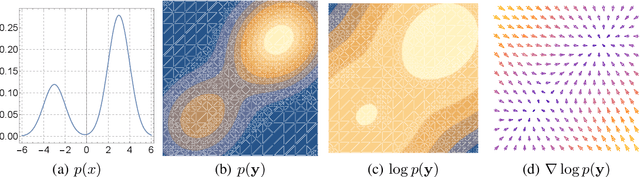
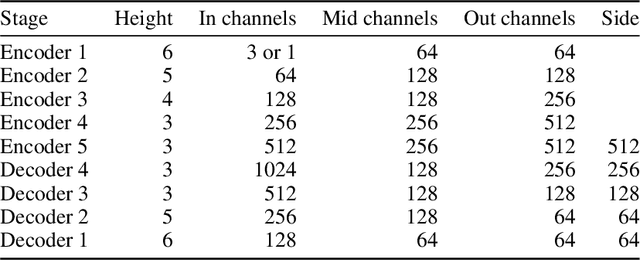
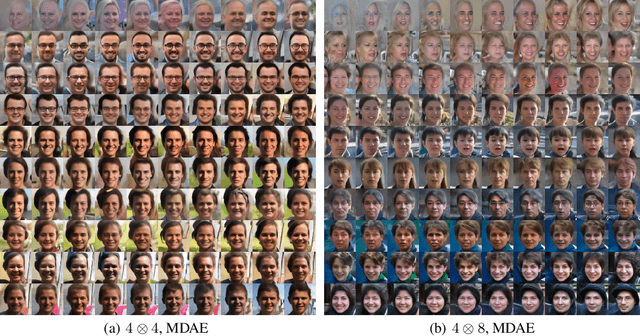
We formally map the problem of sampling from an unknown distribution with density $p_X$ in $\mathbb{R}^d$ to the problem of learning and sampling $p_\mathbf{Y}$ in $\mathbb{R}^{Md}$ obtained by convolving $p_X$ with a fixed factorial kernel: $p_\mathbf{Y}$ is referred to as M-density and the factorial kernel as multimeasurement noise model (MNM). The M-density is smoother than $p_X$, easier to learn and sample from, yet for large $M$ the two problems are mathematically equivalent since $X$ can be estimated exactly given $\mathbf{Y}=\mathbf{y}$ using the Bayes estimator $\widehat{x}(\mathbf{y})=\mathbb{E}[X\vert\mathbf{Y}=\mathbf{y}]$. To formulate the problem, we derive $\widehat{x}(\mathbf{y})$ for Poisson and Gaussian MNMs expressed in closed form in terms of unnormalized $p_\mathbf{Y}$. This leads to a simple least-squares objective for learning parametric energy and score functions. We present various parametrization schemes of interest, including one in which studying Gaussian M-densities directly leads to multidenoising autoencoders--this is the first theoretical connection made between denoising autoencoders and empirical Bayes in the literature. Samples from $p_X$ are obtained by walk-jump sampling (Saremi & Hyvarinen, 2019) via underdamped Langevin MCMC (walk) to sample from $p_\mathbf{Y}$ and the multimeasurement Bayes estimation of $X$ (jump). We study permutation invariant Gaussian M-densities on MNIST, CIFAR-10, and FFHQ-256 datasets, and demonstrate the effectiveness of this framework for realizing fast-mixing stable Markov chains in high dimensions.

Reward-Weighted Regression Converges to a Global Optimum

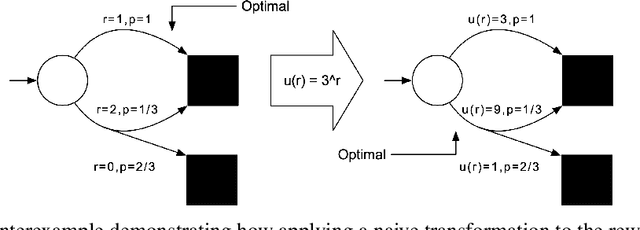
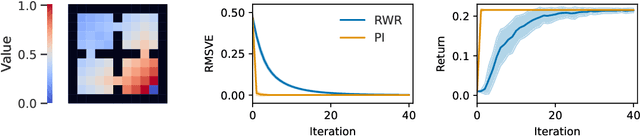
Reward-Weighted Regression (RWR) belongs to a family of widely known iterative Reinforcement Learning algorithms based on the Expectation-Maximization framework. In this family, learning at each iteration consists of sampling a batch of trajectories using the current policy and fitting a new policy to maximize a return-weighted log-likelihood of actions. Although RWR is known to yield monotonic improvement of the policy under certain circumstances, whether and under which conditions RWR converges to the optimal policy have remained open questions. In this paper, we provide for the first time a proof that RWR converges to a global optimum when no function approximation is used.

ClipUp: A Simple and Powerful Optimizer for Distribution-based Policy Evolution

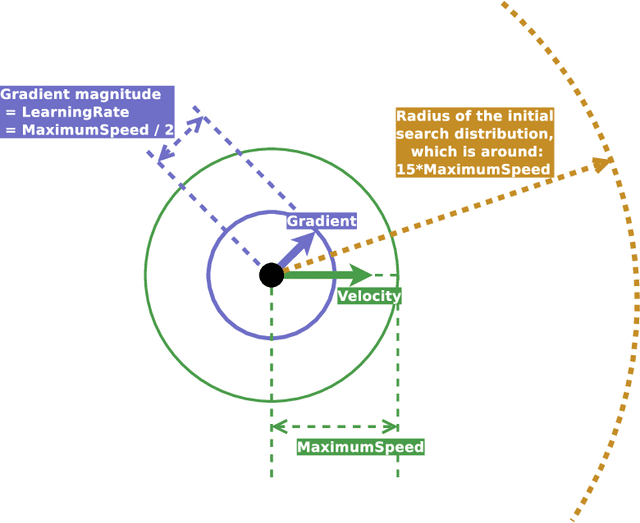
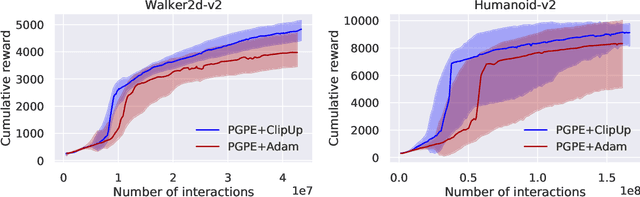
Distribution-based search algorithms are an effective approach for evolutionary reinforcement learning of neural network controllers. In these algorithms, gradients of the total reward with respect to the policy parameters are estimated using a population of solutions drawn from a search distribution, and then used for policy optimization with stochastic gradient ascent. A common choice in the community is to use the Adam optimization algorithm for obtaining an adaptive behavior during gradient ascent, due to its success in a variety of supervised learning settings. As an alternative to Adam, we propose to enhance classical momentum-based gradient ascent with two simple techniques: gradient normalization and update clipping. We argue that the resulting optimizer called ClipUp (short for "clipped updates") is a better choice for distribution-based policy evolution because its working principles are simple and easy to understand and its hyperparameters can be tuned more intuitively in practice. Moreover, it removes the need to re-tune hyperparameters if the reward scale changes. Experiments show that ClipUp is competitive with Adam despite its simplicity and is effective on challenging continuous control benchmarks, including the Humanoid control task based on the Bullet physics simulator.

Training Agents using Upside-Down Reinforcement Learning

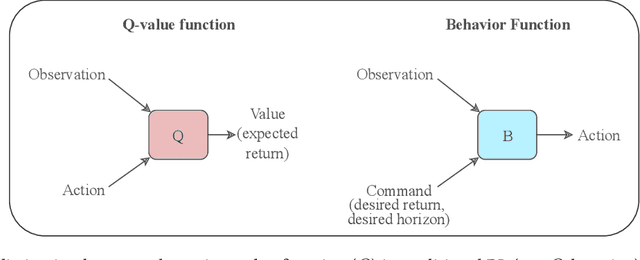
Traditional Reinforcement Learning (RL) algorithms either predict rewards with value functions or maximize them using policy search. We study an alternative: Upside-Down Reinforcement Learning (Upside-Down RL or UDRL), that solves RL problems primarily using supervised learning techniques. Many of its main principles are outlined in a companion report [34]. Here we present the first concrete implementation of UDRL and demonstrate its feasibility on certain episodic learning problems. Experimental results show that its performance can be surprisingly competitive with, and even exceed that of traditional baseline algorithms developed over decades of research.