Multimodal Quantum Vision Transformer for Enzyme Commission Classification from Biochemical Representations

Accurately predicting enzyme functionality remains one of the major challenges in computational biology, particularly for enzymes with limited structural annotations or sequence homology. We present a novel multimodal Quantum Machine Learning (QML) framework that enhances Enzyme Commission (EC) classification by integrating four complementary biochemical modalities: protein sequence embeddings, quantum-derived electronic descriptors, molecular graph structures, and 2D molecular image representations. Quantum Vision Transformer (QVT) backbone equipped with modality-specific encoders and a unified cross-attention fusion module. By integrating graph features and spatial patterns, our method captures key stereoelectronic interactions behind enzyme function. Experimental results demonstrate that our multimodal QVT model achieves a top-1 accuracy of 85.1%, outperforming sequence-only baselines by a substantial margin and achieving better performance results compared to other QML models.

Enhancing Quantum Federated Learning with Fisher Information-Based Optimization

Federated Learning (FL) has become increasingly popular across different sectors, offering a way for clients to work together to train a global model without sharing sensitive data. It involves multiple rounds of communication between the global model and participating clients, which introduces several challenges like high communication costs, heterogeneous client data, prolonged processing times, and increased vulnerability to privacy threats. In recent years, the convergence of federated learning and parameterized quantum circuits has sparked significant research interest, with promising implications for fields such as healthcare and finance. By enabling decentralized training of quantum models, it allows clients or institutions to collaboratively enhance model performance and outcomes while preserving data privacy. Recognizing that Fisher information can quantify the amount of information that a quantum state carries under parameter changes, thereby providing insight into its geometric and statistical properties. We intend to leverage this property to address the aforementioned challenges. In this work, we propose a Quantum Federated Learning (QFL) algorithm that makes use of the Fisher information computed on local client models, with data distributed across heterogeneous partitions. This approach identifies the critical parameters that significantly influence the quantum model's performance, ensuring they are preserved during the aggregation process. Our research assessed the effectiveness and feasibility of QFL by comparing its performance against other variants, and exploring the benefits of incorporating Fisher information in QFL settings. Experimental results on ADNI and MNIST datasets demonstrate the effectiveness of our approach in achieving better performance and robustness against the quantum federated averaging method.

PearSAN: A Machine Learning Method for Inverse Design using Pearson Correlated Surrogate Annealing

PearSAN is a machine learning-assisted optimization algorithm applicable to inverse design problems with large design spaces, where traditional optimizers struggle. The algorithm leverages the latent space of a generative model for rapid sampling and employs a Pearson correlated surrogate model to predict the figure of merit of the true design metric. As a showcase example, PearSAN is applied to thermophotovoltaic (TPV) metasurface design by matching the working bands between a thermal radiator and a photovoltaic cell. PearSAN can work with any pretrained generative model with a discretized latent space, making it easy to integrate with VQ-VAEs and binary autoencoders. Its novel Pearson correlational loss can be used as both a latent regularization method, similar to batch and layer normalization, and as a surrogate training loss. We compare both to previous energy matching losses, which are shown to enforce poor regularization and performance, even with upgraded affine parameters. PearSAN achieves a state-of-the-art maximum design efficiency of 97%, and is at least an order of magnitude faster than previous methods, with an improved maximum figure-of-merit gain.

Multi-Omic and Quantum Machine Learning Integration for Lung Subtypes Classification

Quantum Machine Learning (QML) is a red-hot field that brings novel discoveries and exciting opportunities to resolve, speed up, or refine the analysis of a wide range of computational problems. In the realm of biomedical research and personalized medicine, the significance of multi-omics integration lies in its ability to provide a thorough and holistic comprehension of complex biological systems. This technology links fundamental research to clinical practice. The insights gained from integrated omics data can be translated into clinical tools for diagnosis, prognosis, and treatment planning. The fusion of quantum computing and machine learning holds promise for unraveling complex patterns within multi-omics datasets, providing unprecedented insights into the molecular landscape of lung cancer. Due to the heterogeneity, complexity, and high dimensionality of multi-omic cancer data, characterized by the vast number of features (such as gene expression, micro-RNA, and DNA methylation) relative to the limited number of lung cancer patient samples, our prime motivation for this paper is the integration of multi-omic data, unique feature selection, and diagnostic classification of lung subtypes: lung squamous cell carcinoma (LUSC-I) and lung adenocarcinoma (LUAD-II) using quantum machine learning. We developed a method for finding the best differentiating features between LUAD and LUSC datasets, which has the potential for biomarker discovery.

Non-native Quantum Generative Optimization with Adversarial Autoencoders

Large-scale optimization problems are prevalent in several fields, including engineering, finance, and logistics. However, most optimization problems cannot be efficiently encoded onto a physical system because the existing quantum samplers have too few qubits. Another typical limiting factor is that the optimization constraints are not compatible with the native cost Hamiltonian. This work presents a new approach to address these challenges. We introduce the adversarial quantum autoencoder model (AQAM) that can be used to map large-scale optimization problems onto existing quantum samplers while simultaneously optimizing the problem through latent quantum-enhanced Boltzmann sampling. We demonstrate the AQAM on a neutral atom sampler, and showcase the model by optimizing 64px by 64px unit cells that represent a broad-angle filter metasurface applicable to improving the coherence of neutral atom devices. Using 12-atom simulations, we demonstrate that the AQAM achieves a lower Renyi divergence and a larger spectral gap when compared to classical Markov Chain Monte Carlo samplers. Our work paves the way to more efficient mapping of conventional optimization problems into existing quantum samplers.

Dimension reduction and redundancy removal through successive Schmidt decompositions

Quantum computers are believed to have the ability to process huge data sizes which can be seen in machine learning applications. In these applications, the data in general is classical. Therefore, to process them on a quantum computer, there is a need for efficient methods which can be used to map classical data on quantum states in a concise manner. On the other hand, to verify the results of quantum computers and study quantum algorithms, we need to be able to approximate quantum operations into forms that are easier to simulate on classical computers with some errors. Motivated by these needs, in this paper we study the approximation of matrices and vectors by using their tensor products obtained through successive Schmidt decompositions. We show that data with distributions such as uniform, Poisson, exponential, or similar to these distributions can be approximated by using only a few terms which can be easily mapped onto quantum circuits. The examples include random data with different distributions, the Gram matrices of iris flower, handwritten digits, 20newsgroup, and labeled faces in the wild. And similarly, some quantum operations such as quantum Fourier transform and variational quantum circuits with a small depth also may be approximated with a few terms that are easier to simulate on classical computers. Furthermore, we show how the method can be used to simplify quantum Hamiltonians: In particular, we show the application to randomly generated transverse field Ising model Hamiltonians. The reduced Hamiltonians can be mapped into quantum circuits easily and therefore can be simulated more efficiently.

A Relative Church-Turing-Deutsch Thesis from Special Relativity and Undecidability

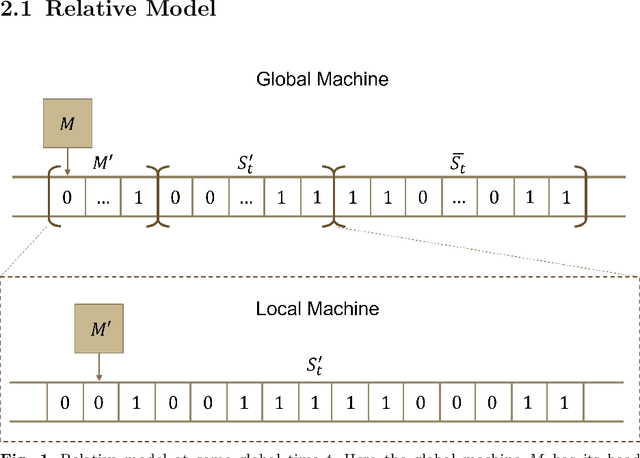
Beginning with Turing's seminal work in 1950, artificial intelligence proposes that consciousness can be simulated by a Turing machine. This implies a potential theory of everything where the universe is a simulation on a computer, which begs the question of whether we can prove we exist in a simulation. In this work, we construct a relative model of computation where a computable \textit{local} machine is simulated by a \textit{global}, classical Turing machine. We show that the problem of the local machine computing \textbf{simulation properties} of its global simulator is undecidable in the same sense as the Halting problem. Then, we show that computing the time, space, or error accumulated by the global simulator are simulation properties and therefore are undecidable. These simulation properties give rise to special relativistic effects in the relative model which we use to construct a relative Church-Turing-Deutsch thesis where a global, classical Turing machine computes quantum mechanics for a local machine with the same constant-time local computational complexity as experienced in our universe.

Training a quantum annealing based restricted Boltzmann machine on cybersecurity data

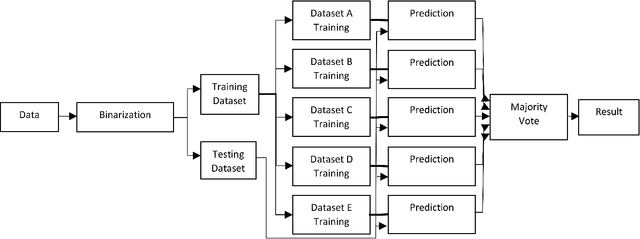
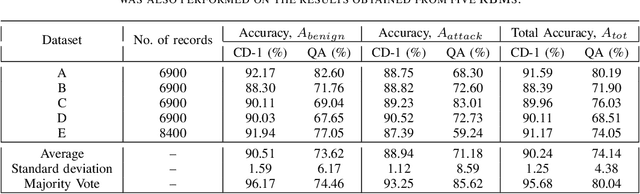
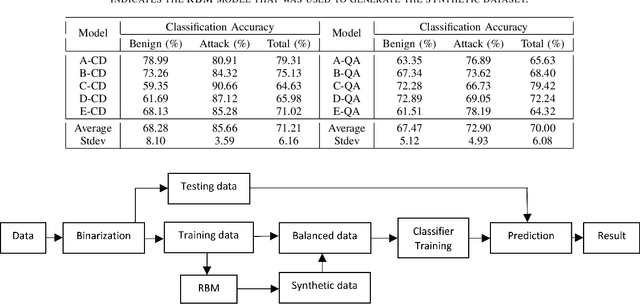
We present a real-world application that uses a quantum computer. Specifically, we trained a Restricted Boltzmann Machine (RBM) using quantum annealing (QA) to develop an intrusion detection system. RBMs were trained on the ISCX data, which is a benchmark dataset for cybersecurity. For comparison, RBMs were also trained using contrastive divergence (CD) which is a classical method. D-Wave's 2000Q quantum annealer has been used to implement QA. Our analysis of the ISCX data shows that the dataset is imbalanced and we present two different schemes to balance the training dataset before feeding it to a classifier. The first scheme is based on the oversampling of attack instances. The imbalanced training dataset was divided into five sub-datasets that were trained separately. A majority voting was performed to get the final result. Our results show the majority vote increased the classification accuracy up from 90.24% to 95.68% in the case of CD. For the case of QA, the classification accuracy increased from 74.14% to 80.04%. In the second scheme, an RBM was used to generate synthetic data to balance the training dataset. The RBMs trained on synthetic data generated from a CD-trained RBM performed comparably to the RBMs trained on synthetic data generated from a QA-trained RBM. Balanced training data was used to evaluate several classifiers. Among the classifiers investigated, K-Nearest Neighbor (KNN) and Neural Network (NN) performed better than other classifiers. They both showed an accuracy of 93%. Our results show a proof of concept that a QA-based RBM can be trained on a binary dataset, with 64-bit records. The illustrative example suggests the possibility to migrate many practical classification problems to QA-based techniques.

Training and Classification using a Restricted Boltzmann Machine on the D-Wave 2000Q

Restricted Boltzmann Machine (RBM) is an energy based, undirected graphical model. It is commonly used for unsupervised and supervised machine learning. Typically, RBM is trained using contrastive divergence (CD). However, training with CD is slow and does not estimate exact gradient of log-likelihood cost function. In this work, the model expectation of gradient learning for RBM has been calculated using a quantum annealer (D-Wave 2000Q), which is much faster than Markov chain Monte Carlo (MCMC) used in CD. Training and classification results are compared with CD. The classification accuracy results indicate similar performance of both methods. Image reconstruction as well as log-likelihood calculations are used to compare the performance of quantum and classical algorithms for RBM training. It is shown that the samples obtained from quantum annealer can be used to train a RBM on a 64-bit `bars and stripes' data set with classification performance similar to a RBM trained with CD. Though training based on CD showed improved learning performance, training using a quantum annealer eliminates computationally expensive MCMC steps of CD.

A Generalized Circuit for the Hamiltonian Dynamics Through the Truncated Series

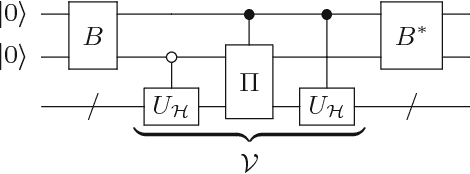
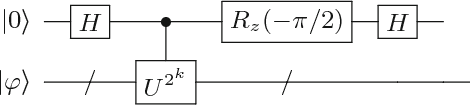
In this paper, we present a method for the Hamiltonian simulation in the context of eigenvalue estimation problems which improves earlier results dealing with Hamiltonian simulation through the truncated Taylor series. In particular, we present a fixed-quantum circuit design for the simulation of the Hamiltonian dynamics, $H(t)$, through the truncated Taylor series method described by Berry et al. \cite{berry2015simulating}. The circuit is general and can be used to simulate any given matrix in the phase estimation algorithm by only changing the angle values of the quantum gates implementing the time variable $t$ in the series. The circuit complexity depends on the number of summation terms composing the Hamiltonian and requires $O(Ln)$ number of quantum gates for the simulation of a molecular Hamiltonian. Here, $n$ is the number of states of a spin orbital, and $L$ is the number of terms in the molecular Hamiltonian and generally bounded by $O(n^4)$. We also discuss how to use the circuit in adaptive processes and eigenvalue related problems along with a slight modified version of the iterative phase estimation algorithm. In addition, a simple divide and conquer method is presented for mapping a matrix which are not given as sums of unitary matrices into the circuit. The complexity of the circuit is directly related to the structure of the matrix and can be bounded by $O(poly(n))$ for a matrix with $poly(n)-$sparsity.