Evaluating the AI-Lab Intervention: Impact on Student Perception and Use of Generative AI in Early Undergraduate Computer Science Courses

Generative AI (GenAI) is rapidly entering computer science education, yet its effects on student learning, skill development, and perceptions remain underexplored. Concerns about overreliance coexist with a gap in research on structured scaffolding to guide tool use in formal courses. This study examines the impact of a dedicated "AI-Lab" intervention -- emphasizing guided scaffolding and mindful engagement -- on undergraduate students in Data Structures and Algorithms, Competitive Programming, and first-year engineering courses at Purdue University. Over three semesters, we integrated AI-Lab modules into four mandatory and elective courses, yielding 831 matched pre- and post-intervention survey responses, alongside focus group discussions. Employing a mixed-methods approach, we analyzed quantitative shifts in usage patterns and attitudes as well as qualitative narratives of student experiences. While the overall frequency of GenAI usage for homework or programming projects remained largely stable, we observed large effect sizes in comfort and openness across conceptual, debugging, and homework problems. Notably, usage patterns for debugging also shifted statistically significantly, reflecting students' more mindful and deliberate approach. Focus group discussions corroborated these results, suggesting that the intervention "bridged the gap" between naive GenAI usage and more nuanced, reflective integration of AI tools into coursework, ultimately heightening students' awareness of their own skill development. These findings suggest that structured, scaffolded interventions can enable students to harness GenAI's benefits without undermining essential competencies. We offer evidence-based recommendations for educators seeking to integrate GenAI responsibly into computing curricula and identify avenues for future research on GenAI-supported pedagogy.

A Relative Church-Turing-Deutsch Thesis from Special Relativity and Undecidability

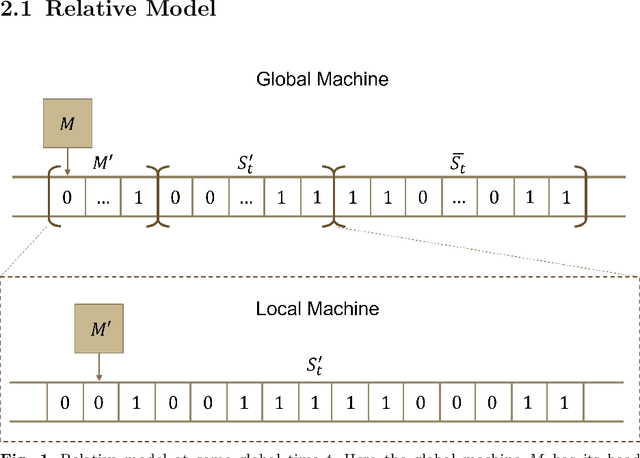
Beginning with Turing's seminal work in 1950, artificial intelligence proposes that consciousness can be simulated by a Turing machine. This implies a potential theory of everything where the universe is a simulation on a computer, which begs the question of whether we can prove we exist in a simulation. In this work, we construct a relative model of computation where a computable \textit{local} machine is simulated by a \textit{global}, classical Turing machine. We show that the problem of the local machine computing \textbf{simulation properties} of its global simulator is undecidable in the same sense as the Halting problem. Then, we show that computing the time, space, or error accumulated by the global simulator are simulation properties and therefore are undecidable. These simulation properties give rise to special relativistic effects in the relative model which we use to construct a relative Church-Turing-Deutsch thesis where a global, classical Turing machine computes quantum mechanics for a local machine with the same constant-time local computational complexity as experienced in our universe.