Recurrent Self-Attention Dynamics: An Energy-Agnostic Perspective from Jacobians

The theoretical understanding of self-attention (SA) has been steadily progressing. A prominent line of work studies a class of SA layers that admit an energy function decreased by state updates. While it provides valuable insights into inherent biases in signal propagation, it often relies on idealized assumptions or additional constraints not necessarily present in standard SA. Thus, to broaden our understanding, this work aims to relax these energy constraints and provide an energy-agnostic characterization of inference dynamics by dynamical systems analysis. In more detail, we first consider relaxing the symmetry and single-head constraints traditionally required in energy-based formulations. Next, to investigate more general SA architectures capable of oscillatory dynamics without necessarily admitting an energy function, we analyze the Jacobian matrix of the state. We reveal that normalization layers effectively normalize the Jacobian's complex eigenvalues, forcing the dynamics close to a critical state. This significantly enhances inference performance. Furthermore, we utilize the Jacobian perspective to develop regularization methods for training and a pseudo-energy for monitoring inference dynamics.

Local Loss Optimization in the Infinite Width: Stable Parameterization of Predictive Coding Networks and Target Propagation

Local learning, which trains a network through layer-wise local targets and losses, has been studied as an alternative to backpropagation (BP) in neural computation. However, its algorithms often become more complex or require additional hyperparameters because of the locality, making it challenging to identify desirable settings in which the algorithm progresses in a stable manner. To provide theoretical and quantitative insights, we introduce the maximal update parameterization ($\mu$P) in the infinite-width limit for two representative designs of local targets: predictive coding (PC) and target propagation (TP). We verified that $\mu$P enables hyperparameter transfer across models of different widths. Furthermore, our analysis revealed unique and intriguing properties of $\mu$P that are not present in conventional BP. By analyzing deep linear networks, we found that PC's gradients interpolate between first-order and Gauss-Newton-like gradients, depending on the parameterization. We demonstrate that, in specific standard settings, PC in the infinite-width limit behaves more similarly to the first-order gradient. For TP, even with the standard scaling of the last layer, which differs from classical $\mu$P, its local loss optimization favors the feature learning regime over the kernel regime.

Optimal Layer Selection for Latent Data Augmentation

While data augmentation (DA) is generally applied to input data, several studies have reported that applying DA to hidden layers in neural networks, i.e., feature augmentation, can improve performance. However, in previous studies, the layers to which DA is applied have not been carefully considered, often being applied randomly and uniformly or only to a specific layer, leaving room for arbitrariness. Thus, in this study, we investigated the trends of suitable layers for applying DA in various experimental configurations, e.g., training from scratch, transfer learning, various dataset settings, and different models. In addition, to adjust the suitable layers for DA automatically, we propose the adaptive layer selection (AdaLASE) method, which updates the ratio to perform DA for each layer based on the gradient descent method during training. The experimental results obtained on several image classification datasets indicate that the proposed AdaLASE method altered the ratio as expected and achieved high overall test accuracy.

Hierarchical Associative Memory, Parallelized MLP-Mixer, and Symmetry Breaking

Transformers have established themselves as the leading neural network model in natural language processing and are increasingly foundational in various domains. In vision, the MLP-Mixer model has demonstrated competitive performance, suggesting that attention mechanisms might not be indispensable. Inspired by this, recent research has explored replacing attention modules with other mechanisms, including those described by MetaFormers. However, the theoretical framework for these models remains underdeveloped. This paper proposes a novel perspective by integrating Krotov's hierarchical associative memory with MetaFormers, enabling a comprehensive representation of the entire Transformer block, encompassing token-/channel-mixing modules, layer normalization, and skip connections, as a single Hopfield network. This approach yields a parallelized MLP-Mixer derived from a three-layer Hopfield network, which naturally incorporates symmetric token-/channel-mixing modules and layer normalization. Empirical studies reveal that symmetric interaction matrices in the model hinder performance in image recognition tasks. Introducing symmetry-breaking effects transitions the performance of the symmetric parallelized MLP-Mixer to that of the vanilla MLP-Mixer. This indicates that during standard training, weight matrices of the vanilla MLP-Mixer spontaneously acquire a symmetry-breaking configuration, enhancing their effectiveness. These findings offer insights into the intrinsic properties of Transformers and MLP-Mixers and their theoretical underpinnings, providing a robust framework for future model design and optimization.

Self-attention Networks Localize When QK-eigenspectrum Concentrates

The self-attention mechanism prevails in modern machine learning. It has an interesting functionality of adaptively selecting tokens from an input sequence by modulating the degree of attention localization, which many researchers speculate is the basis of the powerful model performance but complicates the underlying mechanism of the learning dynamics. In recent years, mainly two arguments have connected attention localization to the model performances. One is the rank collapse, where the embedded tokens by a self-attention block become very similar across different tokens, leading to a less expressive network. The other is the entropy collapse, where the attention probability approaches non-uniform and entails low entropy, making the learning dynamics more likely to be trapped in plateaus. These two failure modes may apparently contradict each other because the rank and entropy collapses are relevant to uniform and non-uniform attention, respectively. To this end, we characterize the notion of attention localization by the eigenspectrum of query-key parameter matrices and reveal that a small eigenspectrum variance leads attention to be localized. Interestingly, the small eigenspectrum variance prevents both rank and entropy collapse, leading to better model expressivity and trainability.

On the Parameterization of Second-Order Optimization Effective Towards the Infinite Width

Second-order optimization has been developed to accelerate the training of deep neural networks and it is being applied to increasingly larger-scale models. In this study, towards training on further larger scales, we identify a specific parameterization for second-order optimization that promotes feature learning in a stable manner even if the network width increases significantly. Inspired by a maximal update parameterization, we consider a one-step update of the gradient and reveal the appropriate scales of hyperparameters including random initialization, learning rates, and damping terms. Our approach covers two major second-order optimization algorithms, K-FAC and Shampoo, and we demonstrate that our parameterization achieves higher generalization performance in feature learning. In particular, it enables us to transfer the hyperparameters across models with different widths.

MLP-Mixer as a Wide and Sparse MLP

Multi-layer perceptron (MLP) is a fundamental component of deep learning that has been extensively employed for various problems. However, recent empirical successes in MLP-based architectures, particularly the progress of the MLP-Mixer, have revealed that there is still hidden potential in improving MLPs to achieve better performance. In this study, we reveal that the MLP-Mixer works effectively as a wide MLP with certain sparse weights. Initially, we clarify that the mixing layer of the Mixer has an effective expression as a wider MLP whose weights are sparse and represented by the Kronecker product. This expression naturally defines a permuted-Kronecker (PK) family, which can be regarded as a general class of mixing layers and is also regarded as an approximation of Monarch matrices. Subsequently, because the PK family effectively constitutes a wide MLP with sparse weights, one can apply the hypothesis proposed by Golubeva, Neyshabur and Gur-Ari (2021) that the prediction performance improves as the width (sparsity) increases when the number of weights is fixed. We empirically verify this hypothesis by maximizing the effective width of the MLP-Mixer, which enables us to determine the appropriate size of the mixing layers quantitatively.

Attention in a family of Boltzmann machines emerging from modern Hopfield networks

Hopfield networks and Boltzmann machines (BMs) are fundamental energy-based neural network models. Recent studies on modern Hopfield networks have broaden the class of energy functions and led to a unified perspective on general Hopfield networks including an attention module. In this letter, we consider the BM counterparts of modern Hopfield networks using the associated energy functions, and study their salient properties from a trainability perspective. In particular, the energy function corresponding to the attention module naturally introduces a novel BM, which we refer to as attentional BM (AttnBM). We verify that AttnBM has a tractable likelihood function and gradient for a special case and is easy to train. Moreover, we reveal the hidden connections between AttnBM and some single-layer models, namely the Gaussian--Bernoulli restricted BM and denoising autoencoder with softmax units. We also investigate BMs introduced by other energy functions, and in particular, observe that the energy function of dense associative memory models gives BMs belonging to Exponential Family Harmoniums.

Understanding Gradient Regularization in Deep Learning: Efficient Finite-Difference Computation and Implicit Bias

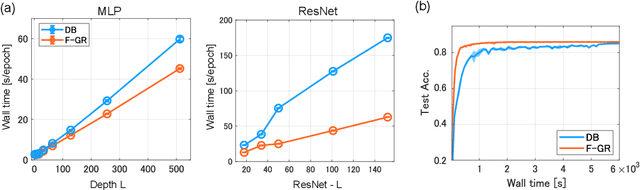
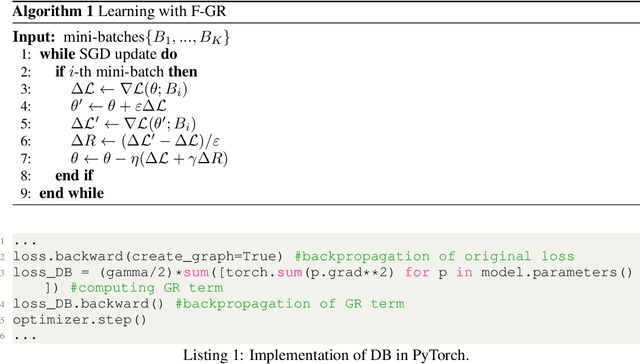
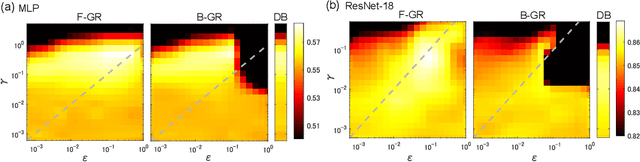
Gradient regularization (GR) is a method that penalizes the gradient norm of the training loss during training. Although some studies have reported that GR improves generalization performance in deep learning, little attention has been paid to it from the algorithmic perspective, that is, the algorithms of GR that efficiently improve performance. In this study, we first reveal that a specific finite-difference computation, composed of both gradient ascent and descent steps, reduces the computational cost for GR. In addition, this computation empirically achieves better generalization performance. Next, we theoretically analyze a solvable model, a diagonal linear network, and clarify that GR has a desirable implicit bias in a certain problem. In particular, learning with the finite-difference GR chooses better minima as the ascent step size becomes larger. Finally, we demonstrate that finite-difference GR is closely related to some other algorithms based on iterative ascent and descent steps for exploring flat minima: sharpness-aware minimization and the flooding method. We reveal that flooding performs finite-difference GR in an implicit way. Thus, this work broadens our understanding of GR in both practice and theory.

Deep Learning in Random Neural Fields: Numerical Experiments via Neural Tangent Kernel

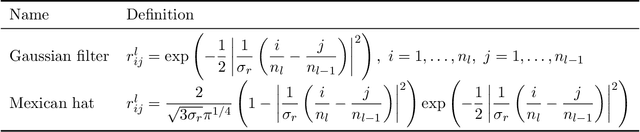
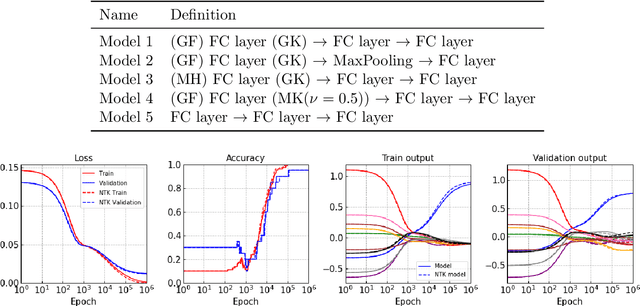
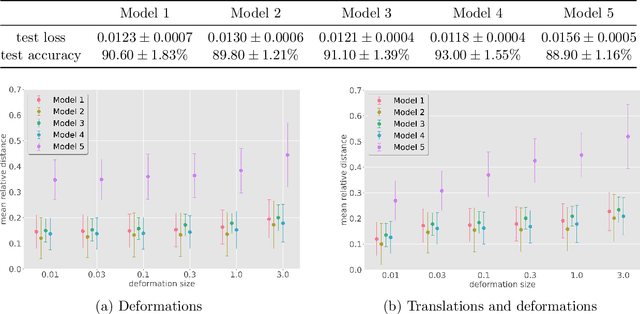
A biological neural network in the cortex forms a neural field. Neurons in the field have their own receptive fields, and connection weights between two neurons are random but highly correlated when they are in close proximity in receptive fields. In this paper, we investigate such neural fields in a multilayer architecture to investigate the supervised learning of the fields. We empirically compare the performances of our field model with those of randomly connected deep networks. The behavior of a randomly connected network is investigated on the basis of the key idea of the neural tangent kernel regime, a recent development in the machine learning theory of over-parameterized networks; for most randomly connected neural networks, it is shown that global minima always exist in their small neighborhoods. We numerically show that this claim also holds for our neural fields. In more detail, our model has two structures: i) each neuron in a field has a continuously distributed receptive field, and ii) the initial connection weights are random but not independent, having correlations when the positions of neurons are close in each layer. We show that such a multilayer neural field is more robust than conventional models when input patterns are deformed by noise disturbances. Moreover, its generalization ability can be slightly superior to that of conventional models.