Taming the Long Tail of Deep Probabilistic Forecasting

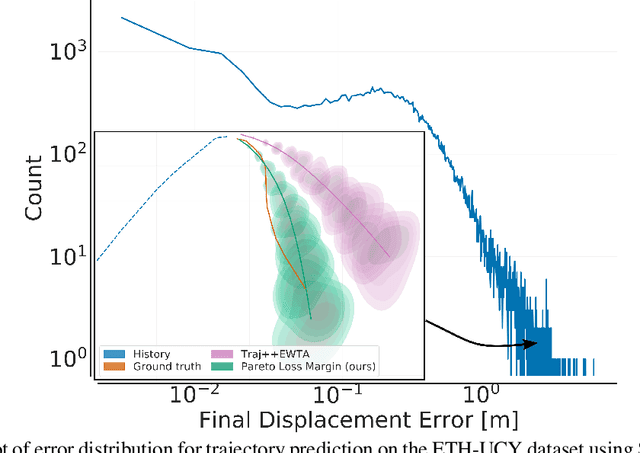
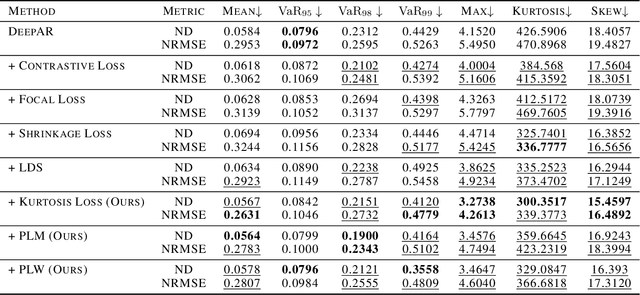
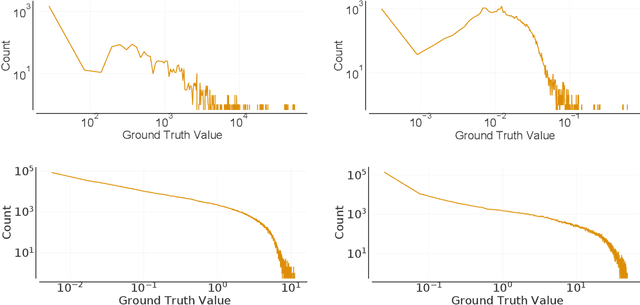
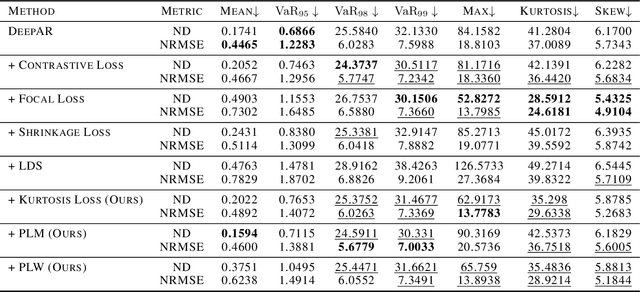
Deep probabilistic forecasting is gaining attention in numerous applications ranging from weather prognosis, through electricity consumption estimation, to autonomous vehicle trajectory prediction. However, existing approaches focus on improvements on the most common scenarios without addressing the performance on rare and difficult cases. In this work, we identify a long tail behavior in the performance of state-of-the-art deep learning methods on probabilistic forecasting. We present two moment-based tailedness measurement concepts to improve performance on the difficult tail examples: Pareto Loss and Kurtosis Loss. Kurtosis loss is a symmetric measurement as the fourth moment about the mean of the loss distribution. Pareto loss is asymmetric measuring right tailedness, modeling the loss using a generalized Pareto distribution (GPD). We demonstrate the performance of our approach on several real-world datasets including time series and spatiotemporal trajectories, achieving significant improvements on the tail examples.

Approximately Equivariant Networks for Imperfectly Symmetric Dynamics

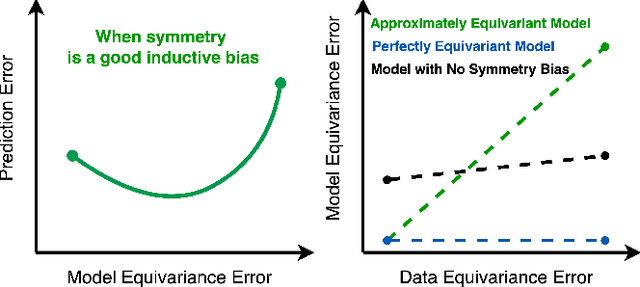
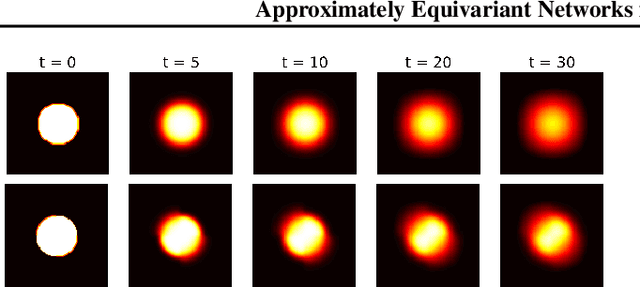
Incorporating symmetry as an inductive bias into neural network architecture has led to improvements in generalization, data efficiency, and physical consistency in dynamics modeling. Methods such as CNN or equivariant neural networks use weight tying to enforce symmetries such as shift invariance or rotational equivariance. However, despite the fact that physical laws obey many symmetries, real-world dynamical data rarely conforms to strict mathematical symmetry either due to noisy or incomplete data or to symmetry breaking features in the underlying dynamical system. We explore approximately equivariant networks which are biased towards preserving symmetry but are not strictly constrained to do so. By relaxing equivariance constraints, we find that our models can outperform both baselines with no symmetry bias and baselines with overly strict symmetry in both simulated turbulence domains and real-world multi-stream jet flow.

AI-Bind: Improving Binding Predictions for Novel Protein Targets and Ligands

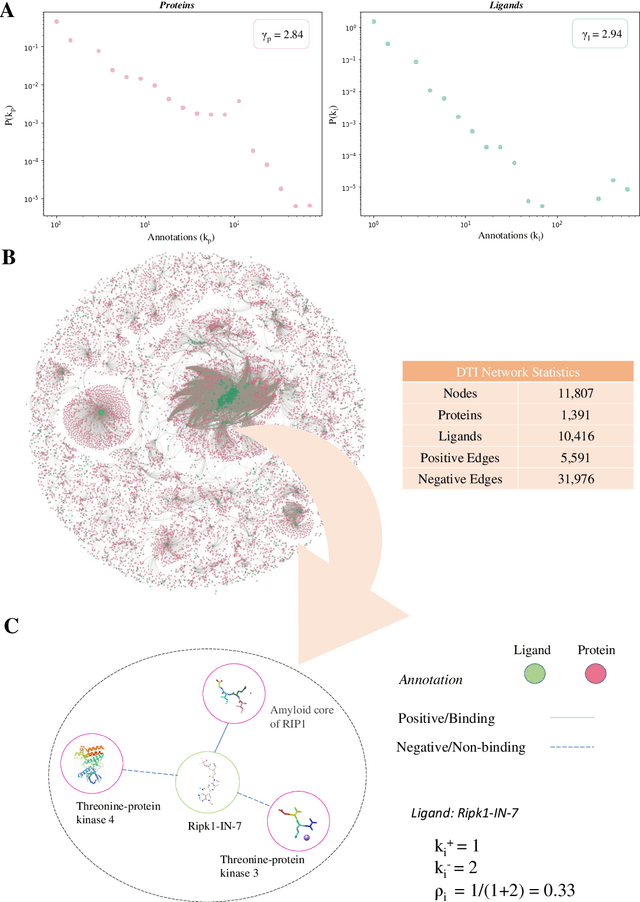
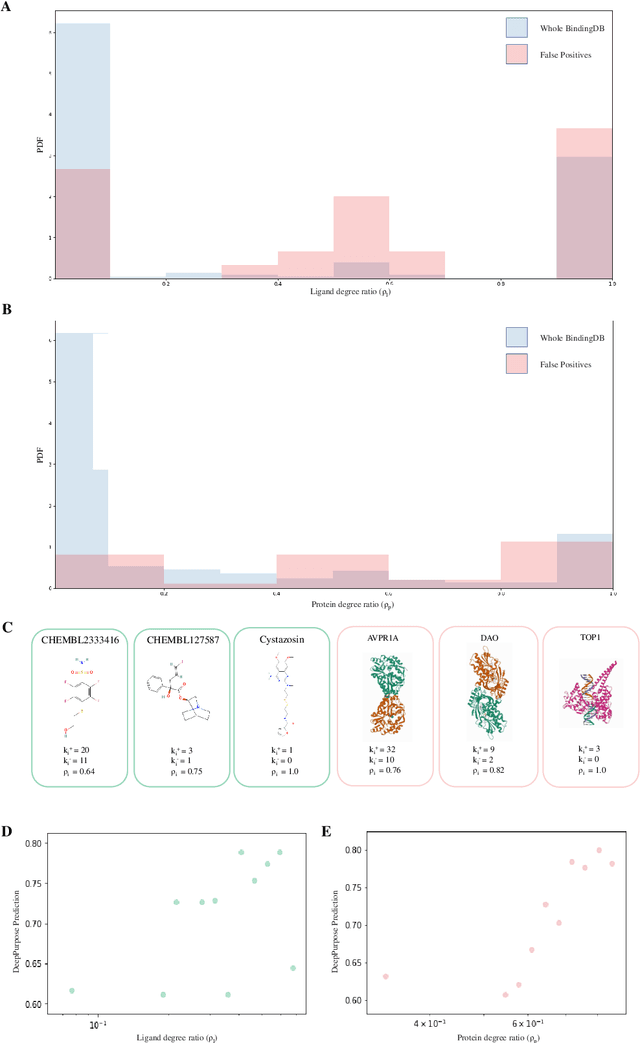
Identifying novel drug-target interactions (DTI) is a critical and rate limiting step in drug discovery. While deep learning models have been proposed to accelerate the identification process, we show that state-of-the-art models fail to generalize to novel (i.e., never-before-seen) structures. We first unveil the mechanisms responsible for this shortcoming, demonstrating how models rely on shortcuts that leverage the topology of the protein-ligand bipartite network, rather than learning the node features. Then, we introduce AI-Bind, a pipeline that combines network-based sampling strategies with unsupervised pre-training, allowing us to limit the annotation imbalance and improve binding predictions for novel proteins and ligands. We illustrate the value of AI-Bind by predicting drugs and natural compounds with binding affinity to SARS-CoV-2 viral proteins and the associated human proteins. We also validate these predictions via auto-docking simulations and comparison with recent experimental evidence. Overall, AI-Bind offers a powerful high-throughput approach to identify drug-target combinations, with the potential of becoming a powerful tool in drug discovery.

Neural Point Process for Learning Spatiotemporal Event Dynamics

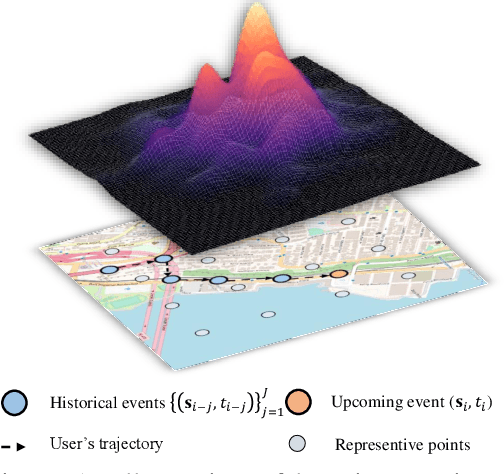
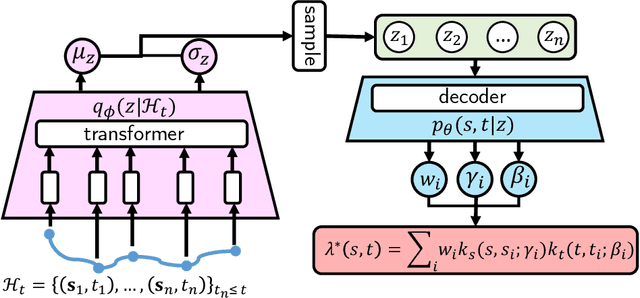
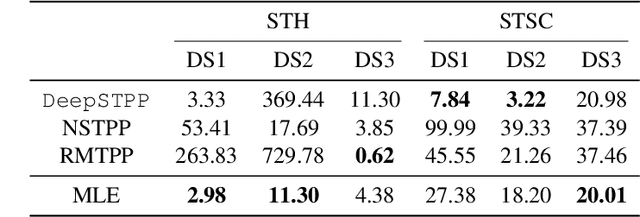
Learning the dynamics of spatiotemporal events is a fundamental problem. Neural point processes enhance the expressivity of point process models with deep neural networks. However, most existing methods only consider temporal dynamics without spatial modeling. We propose Deep Spatiotemporal Point Process (DeepSTPP), a deep dynamics model that integrates spatiotemporal point processes. Our method is flexible, efficient, and can accurately forecast irregularly sampled events over space and time. The key construction of our approach is the nonparametric space-time intensity function, governed by a latent process. The intensity function enjoys closed-form integration for the density. The latent process captures the uncertainty of the event sequence. We use amortized variational inference to infer the latent process with deep networks. Using synthetic datasets, we validate our model can accurately learn the true intensity function. On real-world benchmark datasets, our model demonstrates superior performance over state-of-the-art baselines.

Automatic Symmetry Discovery with Lie Algebra Convolutional Network

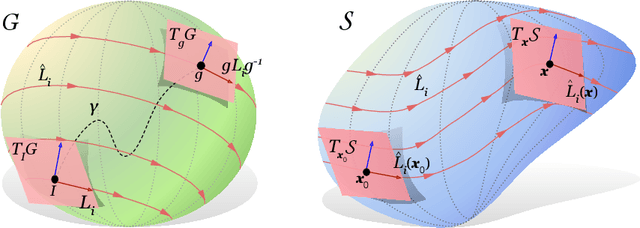
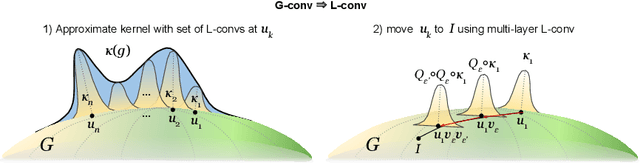
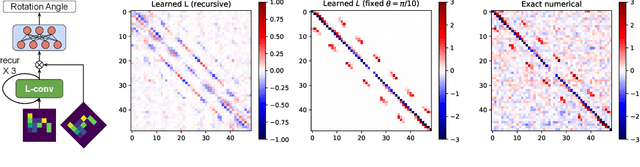
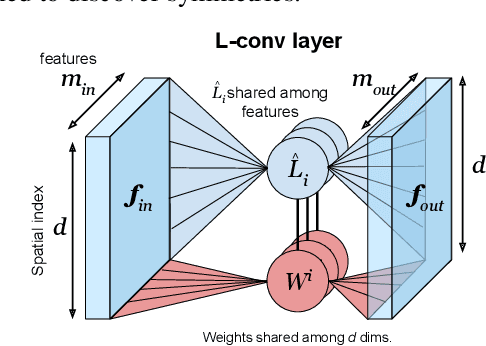
Existing equivariant neural networks for continuous groups require discretization or group representations. All these approaches require detailed knowledge of the group parametrization and cannot learn entirely new symmetries. We propose to work with the Lie algebra (infinitesimal generators) instead of the Lie group.Our model, the Lie algebra convolutional network (L-conv) can learn potential symmetries and does not require discretization of the group. We show that L-conv can serve as a building block to construct any group equivariant architecture. We discuss how CNNs and Graph Convolutional Networks are related to and can be expressed as L-conv with appropriate groups. We also derive the MSE loss for a single L-conv layer and find a deep relation with Lagrangians used in physics, with some of the physics aiding in defining generalization and symmetries in the loss landscape. Conversely, L-conv could be used to propose more general equivariant ans\"atze for scientific machine learning.

Accelerating Stochastic Simulation with Interactive Neural Processes

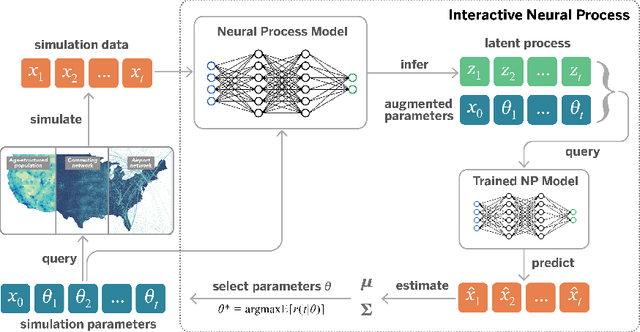
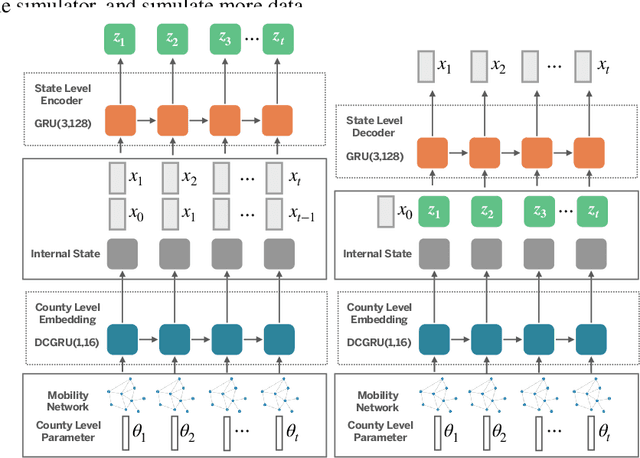
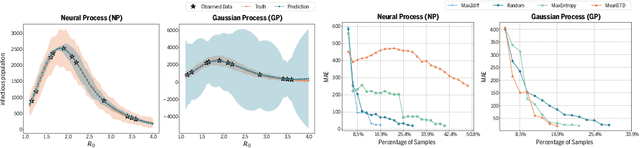
Stochastic simulations such as large-scale, spatiotemporal, age-structured epidemic models are computationally expensive at fine-grained resolution. We propose Interactive Neural Process (INP), an interactive framework to continuously learn a deep learning surrogate model and accelerate simulation. Our framework is based on the novel integration of Bayesian active learning, stochastic simulation and deep sequence modeling. In particular, we develop a novel spatiotemporal neural process model to mimic the underlying process dynamics. Our model automatically infers the latent process which describes the intrinsic uncertainty of the simulator. This also gives rise to a new acquisition function that can quantify the uncertainty of deep learning predictions. We design Bayesian active learning algorithms to iteratively query the simulator, gather more data, and continuously improve the model. We perform theoretical analysis and demonstrate that our approach reduces sample complexity compared with random sampling in high dimension. Empirically, we demonstrate our framework can faithfully imitate the behavior of a complex infectious disease simulator with a small number of examples, enabling rapid simulation and scenario exploration.

Quantifying Uncertainty in Deep Spatiotemporal Forecasting

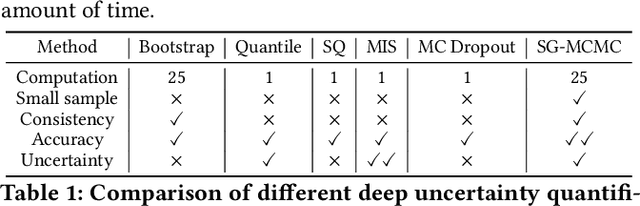
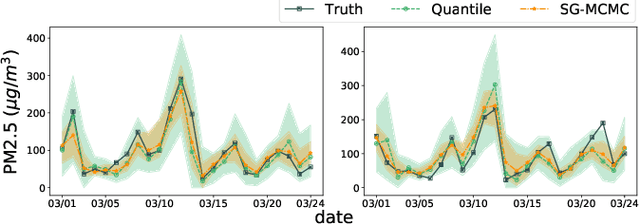
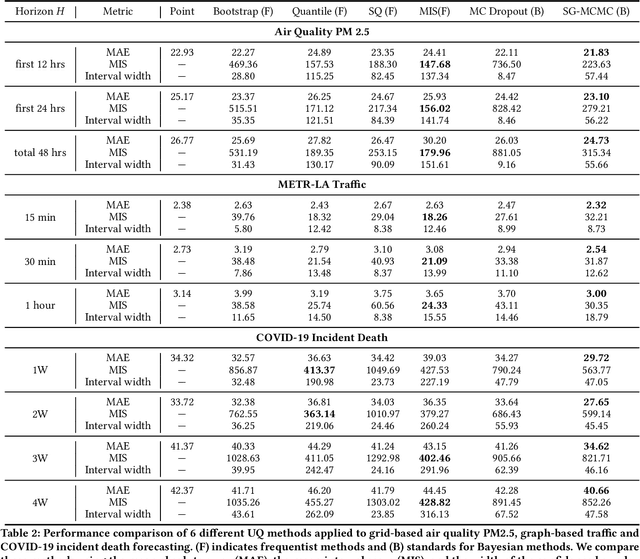
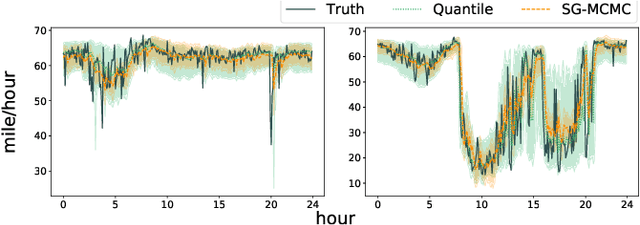
Deep learning is gaining increasing popularity for spatiotemporal forecasting. However, prior works have mostly focused on point estimates without quantifying the uncertainty of the predictions. In high stakes domains, being able to generate probabilistic forecasts with confidence intervals is critical to risk assessment and decision making. Hence, a systematic study of uncertainty quantification (UQ) methods for spatiotemporal forecasting is missing in the community. In this paper, we describe two types of spatiotemporal forecasting problems: regular grid-based and graph-based. Then we analyze UQ methods from both the Bayesian and the frequentist point of view, casting in a unified framework via statistical decision theory. Through extensive experiments on real-world road network traffic, epidemics, and air quality forecasting tasks, we reveal the statistical and computational trade-offs for different UQ methods: Bayesian methods are typically more robust in mean prediction, while confidence levels obtained from frequentist methods provide more extensive coverage over data variations. Computationally, quantile regression type methods are cheaper for a single confidence interval but require re-training for different intervals. Sampling based methods generate samples that can form multiple confidence intervals, albeit at a higher computational cost.

Traffic Forecasting using Vehicle-to-Vehicle Communication

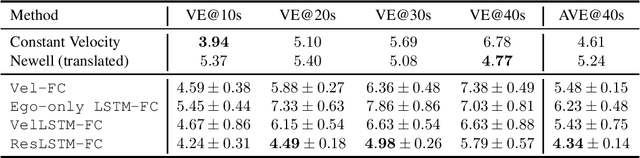
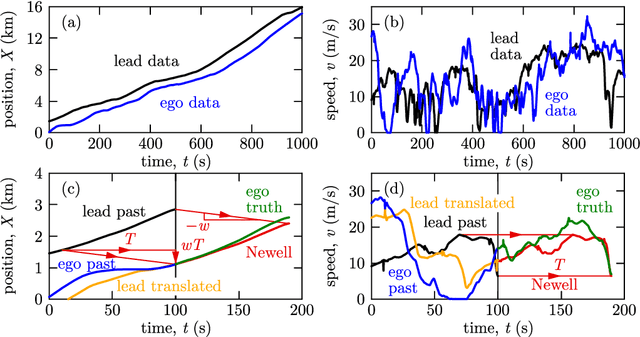
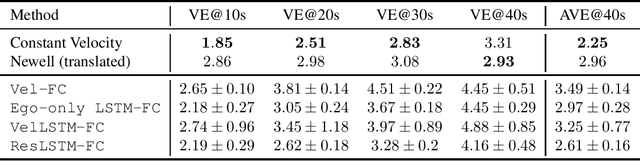
We take the first step in using vehicle-to-vehicle (V2V) communication to provide real-time on-board traffic predictions. In order to best utilize real-world V2V communication data, we integrate first principle models with deep learning. Specifically, we train recurrent neural networks to improve the predictions given by first principle models. Our approach is able to predict the velocity of individual vehicles up to a minute into the future with improved accuracy over first principle-based baselines. We conduct a comprehensive study to evaluate different methods of integrating first principle models with deep learning techniques. The source code for our models is available at https://github.com/Rose-STL-Lab/V2V-traffic-forecast .

Generator Surgery for Compressed Sensing

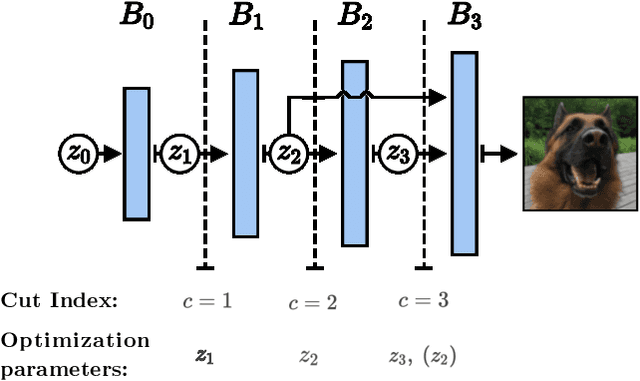
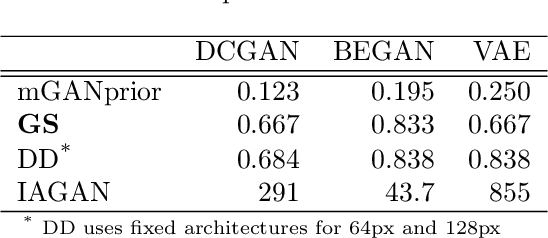
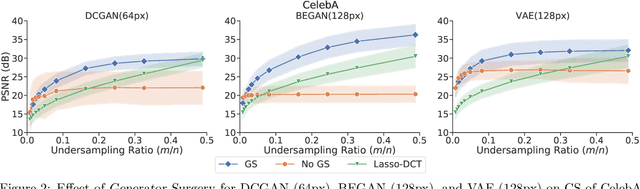
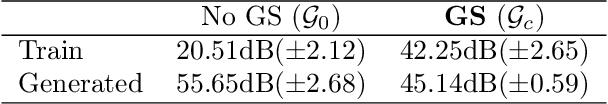
Image recovery from compressive measurements requires a signal prior for the images being reconstructed. Recent work has explored the use of deep generative models with low latent dimension as signal priors for such problems. However, their recovery performance is limited by high representation error. We introduce a method for achieving low representation error using generators as signal priors. Using a pre-trained generator, we remove one or more initial blocks at test time and optimize over the new, higher-dimensional latent space to recover a target image. Experiments demonstrate significantly improved reconstruction quality for a variety of network architectures. This approach also works well for out-of-training-distribution images and is competitive with other state-of-the-art methods. Our experiments show that test-time architectural modifications can greatly improve the recovery quality of generator signal priors for compressed sensing.

Meta-Learning Dynamics Forecasting Using Task Inference

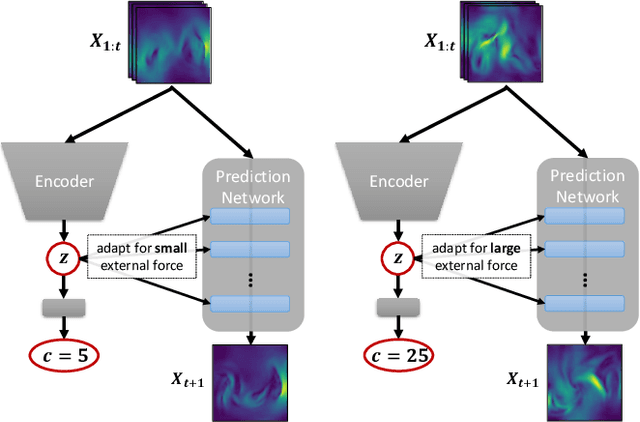
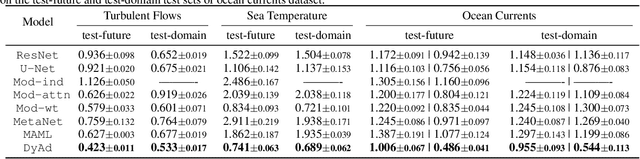
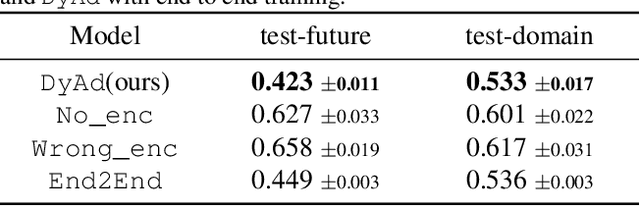
Current deep learning models for dynamics forecasting struggle with generalization. They can only forecast in a specific domain and fail when applied to systems with different parameters, external forces, or boundary conditions. We propose a model-based meta-learning method called DyAd which can generalize across heterogeneous domains by partitioning them into separate subdomains, each with a different task. DyAd has two parts: a prediction network which learns the shared dynamics of the entire domain, and an encoder that infers the parameters of the task. The encoder adapts the prediction network during inference time using adaptive instance normalization and a new layer, AdaPad, specifically designed for boundary conditions. The encoder can also use any weak supervision signals that can help distinguish different tasks, allowing the incorporation of additional domain knowledge. Our model outperforms a variety of state-of-the-art approaches on both turbulent flow and real-world ocean data forecasting tasks.